Бросаем монетку 10 раз какова вероятность что выпадет 9 орлов
Сложные задачи по теории вероятности
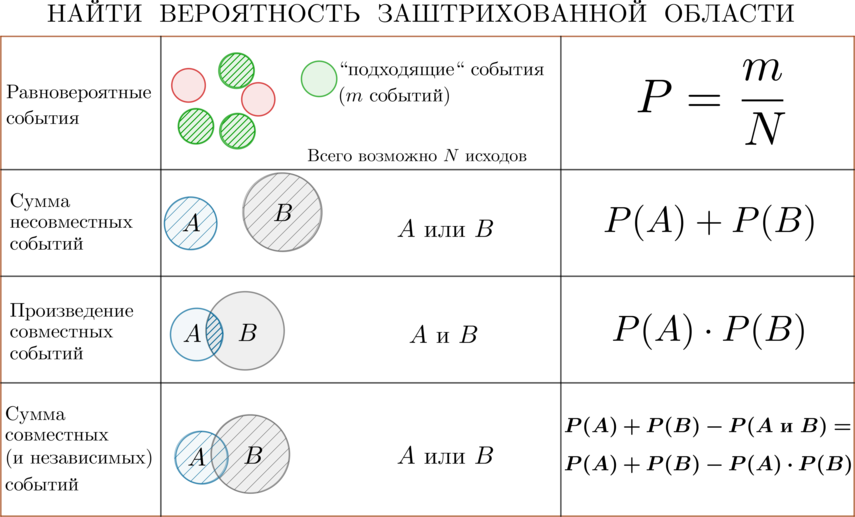
Общая памятка по всем разделам теории вероятностей:
Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть либо ровно 1 решка, либо 0 решек.
Монетку подбросили 3 раза. Какова вероятность того, что выпало не менее 3 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 3 орлов эквивалентно тому, что выпали только орлы.
Монетку подбросили 2 раза. Какова вероятность того, что выпало не менее 1 орла? Ответ округлите до тысячных.
Всевозможных исходов в серии из 2 подбрасываний может быть \(2^2 = 4\) : (Орёл; Орёл), (Орёл; Решка), (Решка; Орёл), (Решка; Решка).
Среди выписанных (всевозможных) исходов под условие задачи подходят первые 3, следовательно, искомая вероятность равна \[\dfrac<3> <4>= 0,75.\]
Условие задачи можно переформулировать в следующем виде: какова вероятность за три подбрасывания получить результаты, остатки от деления на \(3\) которых будут содержать единственный \(0\) и два одинаковых числа?
Таким образом, нас устраивают исходы, остатки от деления на \(3\) которых будут иметь вид:
\[\begin
Если выпускник готовится к сдаче ЕГЭ по математике профильного уровня, ему необходимо научиться решать задачи на применение теории вероятности повышенной сложности. Как показывает практика многих лет, такие задания являются обязательной частью программы аттестационного испытания. Поэтому если учащийся не до конца понимает принцип решения сложных задач на теорию вероятности, ему обязательно стоит вновь разобраться в данной теме.
Вместе с образовательным порталом «Школково» старшеклассники смогут качественно подготовиться к прохождению аттестационного испытания. Наш сайт позволит определить наиболее сложные темы и восполнить пробелы в знаниях. Опытные специалисты «Школково» подготовили весь необходимый материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли легко справиться с решением сложных задач ЕГЭ на теорию вероятности. Базовая информация по данной теме представлена в разделе «Теоретическая справка».
Чтобы попрактиковаться в выполнении сложных задач ЕГЭ по теории вероятности, школьники могут выполнить соответствующие упражнения. Простые и сложные задания, подобранные нашими специалистами, содержат подробные алгоритмы решения и правильные ответы. База заданий регулярно обновляется и дополняется.
Выполнять упражнения школьники из Москвы и других российских городов могут в онлайн-режиме. При необходимости задания по теории вероятности в ЕГЭ можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Бросание монет. Решение задач на нахождение вероятности
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
1. Классическое определение вероятности
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.
Как видим, все довольно просто. Перейдем к чуть более сложной задаче.
Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Взяли разгон и переходим к 4 монетам.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.
2. Комбинаторика + классическая вероятность
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.
Например, если рассмотреть подобную задачу:
Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза
Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).
Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.
Способ 3. Формула Бернулли
А теперь все задачи решаются проще простого, вот глядите!
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.
Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.
Полезные ссылки
Решебник по вероятности
А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):
Монету бросают 10 раз какова вероятность
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
Для задач о подбрасывании монеты существуют два основных метода решения, один – по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй – по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.
1. Классическое определение вероятности
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.
Как видим, все довольно просто. Перейдем к чуть более сложной задаче.
Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Взяли разгон и переходим к 4 монетам.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.
2. Комбинаторика + классическая вероятность
Надо заметить, что если действовать исключительно переборным методом (как это делалось выше), с ростом числа монет быстро растет число комбинаций (для 5 монет – 32, для 6 монет – 64 и так далее), так что и вероятность ошибиться при выписывании исходов велика, метод решения теряет свою простоту и привлекательность.
Один из способов решения этой проблемы – остаться в рамках формулы классической вероятности, но использовать комбинаторные методы (см. формулы комбинаторики тут) для подсчета числа исходов. Поясню на примере последней задачи, решив ее другим способом.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.
Например, если рассмотреть подобную задачу:
Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза
Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).
Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.
Способ 3. Формула Бернулли
А теперь все задачи решаются проще простого, вот глядите!
Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.
Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.
Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.
Полезные ссылки
Решебник по вероятности
А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):
Монета брошена 10 раз. Найти вероятность того, что герб выпадет: а) от 4-х до 6-ти раз; б) хотя бы один раз.
Решение. События выпадения герба при многократном бросании монеты являются независимыми. В каждом испытании герб, так же, как и надпись, выпадает с вероятностью р = 0,5. Таким образом, задача относит-ся к схеме и формуле Бернулли. Для случая а) искомая вероятность вычисле-ния по формуле (2.4), а для случая б) – по формуле (2.3). С помощью этих формул, с учетом того, что р = 0,5 и q = 0,5 получим:
б) р10(хотя бы один раз) = 1 – q 10 = 1 – 1/1024=1023/1024.
нПОЕФХ ВТПУБАФ 10 ТБЪ. оБКДЙФЕ ЧЕТПСФОПУФШ ФПЗП, ЮФП ОЙ ТБЪХ ОЕ ЧЩРБДХФ ДЧБ ПТМБ РПДТСД.
тЕЫЕОЙЕ
рЕТЧЩК УРПУПВ. еУМЙ ПТМПЧ ОЕФ ЧПЧУЕ, ФП ФБЛБС РПУМЕДПЧБФЕМШОПУФШ УПУФПЙФ ЙЪ ДЕУСФЙ ТЕЫЕЛ Й ЧУЕЗП ПДОБ. еУМЙ ПТЕМ ПДЙО, ФП ФБЛЙИ ЛПНВЙОБГЙК 10 (ПТЕМ УФПЙФ ОБ МАВПН ЙЪ 10 НЕУФ). еУМЙ ПТМПЧ ДЧБ, ФП ЛПНВЙОБГЙК (НЩ УЮЙФБЕН ЛПМЙЮЕУФЧП ЧБТЙБОФПЧ ТБУУФБЧЙФШ 2 ПТМБ РП ПДОПНХ НЕЦДХ 8 ТЕЫЛБНЙ ЙМЙ РП ЛТБСН). й ФБЛ ДБМЕЕ. еУМЙ ПТМПЧ k, ФП ЛПНВЙОБГЙК (ЮЙУМП ЧБТЙБОФПЧ ТБУУФБЧЙФШ ПТМПЧ Ч 11 – k НЕУФ НЕЦДХ ТЕЫЛБНЙ Й РП ЛТБСН).
ъОБЮЙФ, ПВЭЕЕ ЮЙУМП ЛПНВЙОБГЙК ТБЧОП
уМЕДПЧБФЕМШОП, ЙУЛПНБС ЧЕТПСФОПУФШ ЕУФШ 144 : 2 10 = 9 /64.
пФЧЕФ
йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
| ПМЙНРЙБДБ | |
| оБЪЧБОЙЕ | ъБПЮОБС ПМЙНРЙБДБ РП ФЕПТЙЙ ЧЕТПСФОПУФЕК Й УФБФЙУФЙЛЕ |
| ЗПД | |
| дБФБ | 2009 |
| ЪБДБЮБ | |
| оПНЕТ | 13 |
Теория вероятностей (ЕГЭ 2022)
Есть какая-то вероятность, что ты сорвешь в лотерее джек-пот. Для этого нужно купить один лотерейный билет.
Кстати, а какова вероятность выиграть, купив один лотерейный билет? А что если купить 2 билета? На сколько повысится вероятность того, что ты выиграешь джек-пот?
А если купить 100 или 1000 билетов? (спойлер: твои шансы сильно не увеличатся, так что если покупаешь билет, бери один).
Вот об этом сегодняшняя статья.
Теория вероятности — коротко о главном
Вероятность – это отношение количества благоприятных событий к количеству всех возможных событий.
Независимые события
Два события независимы, если при наступлении одного вероятность наступления другого не изменяется.
Полная вероятность
Вероятность всех возможных событий равна \( 1\) (\( 100\%\)).
Вероятность того, что событие не произойдет, равна \( 1\) минус вероятность того, что событие произойдет.
Правило умножения вероятностей независимых событий
Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий
Несовместные события
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента. Ряд несовместных событий образуют полную группу событий.
Вероятности несовместных событий складываются.
Описав что должно произойти, используя союзы «И» или «ИЛИ»
Вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.
Теория вероятности — подробнее
Что такое вероятность?
Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от \( 1\) до \( 6\).
Итак, мы бросаем кость и хотим, чтобы выпало \( 5\) или \( 6\). И нам выпадает \( 5\).
В теории вероятностей говорят, что произошло благоприятное событие.
Если бы выпало \( 6\), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.
А сколько неблагоприятных?
Раз всего возможных событий \( 6\), значит, неблагоприятных из них \( 6-2=4\) события (это если выпадет \( 1,\text< >2,\text< >3\) или \( 4\)).
Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.
То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.
Обозначают вероятность латинской буквой \( p\) (видимо, от английского слова probability — вероятность).
Принято измерять вероятность в процентах (см. темы «Дроби, рациональные числа» и «Проценты»).
Для этого значение вероятности нужно умножать на \( 100\%\).
В примере с игральной костью вероятность \( p=\frac<благоприятных><всего>=\frac<2><6>=\frac<1><3>\).
А в процентах: \( p=\frac<1><3>\cdot 100\%=\frac<100><3>\%\approx 33,3\%\).
Примеры
Ответы:
И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.
Зависимые события
Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой \( 3\) двери на выбор.
Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры \( 3\), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.
Но каков этот шанс?
Дверей \( 3\), нужная дверь \( 1\). Вероятность угадать, позвонив в первую дверь: \( \frac<1><3>\). То есть один раз из трех ты точно угадаешь.
Мы хотим узнать, позвонив \( 1\) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:
1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь
А теперь рассмотрим все варианты, где может находиться друг:
а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью
Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.
Как видишь, всего возможно \( 9\) вариантов местоположения друга и твоего выбора, в какую дверь звонить.
А благоприятных исходов всего \( 3\). То есть \( 3\) раза из \( 9\) ты угадаешь, позвонив в дверь \( 1\) раз, т.е. \( \frac<3><9>=\frac<1><3>\).
Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.
Определение – это и есть формула. Вероятность принято обозначать p, поэтому:
Такую формулу писать не очень удобно, поэтому примем за \( \displaystyle <
Вероятность можно записывать в процентах, для этого нужно умножить получившийся результат на \( 100\%\):
Наверное, тебе бросилось в глаза слово «исходы».
Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.
Ну а исходы бывают благоприятные и неблагоприятные.
Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?
Если ты подумал, что \( \displaystyle \frac<1><3>\), то это ошибка. Давай разбираться.
У нас осталось две двери. Таким образом, у нас есть возможные шаги:
1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь
Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):
а. Друг за 1-ой дверью
б. Друг за 2-ой дверью
Давай снова нарисуем таблицу:
Как видишь, всего есть \( 4\) варианта, \( 2\) из которых – благоприятны. То есть вероятность равна \( \displaystyle \frac<2><4>=\frac<1><2>\).
А почему не \( \displaystyle \frac<1><3>\)?
Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.
А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?
Но если есть зависимые события, то должны быть и независимые? Верно, бывают.
Независимые события
Два события независимы, если при наступлении одного вероятность наступления другого не изменяется.
Хрестоматийный пример – бросание монетки.
Бросаем монетку \( 1\) раз. Какова вероятность того, что выпадет, например, орел?
Правильно: \( \displaystyle \frac<1><2>\), ведь вариантов всего \( 2\) (либо орел, либо решка, пренебрежем вероятностью монетки встать на ребро), а устраивает нас только \( 1\).
Но выпала решка. Ладно, бросаем еще раз. Какова сейчас вероятность выпадения орла? Ничего не изменилось, все так же \( \displaystyle \frac<1><2>\).
Сколько вариантов? Два. А сколько нас устраивает? Один.
И пусть хоть тысячу раз подряд будет выпадать решка. Вероятность выпадения орла на \( \displaystyle 1001-й\) раз будет все также \( \displaystyle \frac<1><2>\).
Вариантов всегда \( 2\), а благоприятных – \( 1\).
Отличить зависимые события от независимых легко:
Если эксперимент проводится \( 1\) раз (\( 1\) раз бросают монетку, 1 раз звонят в дверь и т.д.), то события всегда независимые.
Если эксперимент проводится несколько раз (монетку бросают \( 5\) раз, в дверь звонят несколько раз), то первое событие всегда независимое. А дальше, если количество благоприятных или количество всех исходов меняется, то события зависимые, а если нет – независимые.
Ошибка игрока или ложный вывод Монте-Карло
Знаешь, то, что я описал сверху, очень хорошо отражает явление под названием ложный вывод Монте-Карло.
Попробуй придумать и записать на листочке результаты подбрасывания монетки.
А потом попробуй действительно подбрасывать монетку и записывать результат.
Спорим, я без труда определю, какую последовательность ты выдумал?
В реальной последовательности может абсолютно спокойно выпасть 18 решек подряд. А вот ты, составляя последовательность, когда-нибудь точно подумаешь: «Так, что-то многовато решек уже, пора бы и орлу появиться»
В этом и заключается ложный вывод Монте-Карло. В знаменитом казино Монте-Карло люди часто думают, что следующее событие как-то связано с предыдущим, например, ставят на красное, если ранее много раз выпало черное.
В действительности это не так.
А теперь давай немного потренируемся определять вероятность.
Пример 1
Монетку бросают два раза. Какова вероятность того, что два раза подряд выпадет орел?
Решение
Рассмотрим все возможные варианты:
Как видишь, всего варианта \( 4\). Из них нас устраивает только \( 1\). То есть вероятность:
Если в условии просят просто найти вероятность, то ответ нужно давать в виде десятичной дроби. Если было бы указано, что ответ нужно дать в процентах, тогда мы умножили бы на \( 100\%\).
Ответ: \( \displaystyle 0,25\)
Пример 2
В коробке конфет все конфеты упакованы в одинаковую обертку. Однако из \( 20\) конфет – \( 6\) с орехами, \( 5\) с коньяком, \( 4\) с вишней, \( 3\) с карамелью и \( 2\) с нугой.
Какова вероятность, взяв одну конфету, достать конфету с орехами. Ответ дайте в процентах.
Решение:
Сколько всего возможных исходов? \( 6+5+4+3+2=20\).
То есть, взяв одну конфету, она будет одной из \( 20\), имеющихся в коробке.
А сколько благоприятных исходов?
\( 6\), потому что в коробке только \( 6\) конфет с орехами.
\( \displaystyle p=\frac
Ответ: \( \displaystyle 30\)
Пример 3
В коробке \( 20\) шаров. \( 12\) из них белые, \( 8\) – черные.
Решение:
1. В коробке всего \( \displaystyle N=20\) шаров. Из них \( \displaystyle <
2. Теперь шаров в коробке стало: \( \displaystyle N=20+10=30\).
А белых осталось столько же: \( \displaystyle <
\( \displaystyle p=\frac<<
Ответы:
Полная вероятность
Вероятность всех возможных событий равна \( 1\) (\( 100\%\)).
Действительно, если мы будем считать, что все события для нас благоприятны, вероятность благоприятного исхода будет равна \( \displaystyle 1(100\%)\).
Допустим, в ящике \( \displaystyle 4\) красных и \( \displaystyle 5\) зеленых шаров. Какова вероятность вытащить красный шар? Зеленый шар? Красный или зеленый шар?
Вероятность вытащить красный шар:
Красный или зеленый шар:
Как видишь, сумма всех возможных событий равна \( 1\) (\( \displaystyle <
_<к>>+<
_<з>>=\frac<4><9>+\frac<5><9>=\frac<9><9>\)).
Понимание этого момента поможет тебе решить многие задачи.
Пример 4
В ящике лежит \( \displaystyle 10\) фломастеров: \( \displaystyle 3\) зеленых, \( \displaystyle 2\) красных, \( \displaystyle 2\) синих, \( \displaystyle 2\) желтых, \( \displaystyle 1\) черный.
Какова вероятность вытащить НЕ красный фломастер?
Решение:
Давай посчитаем количество благоприятных исходов.
НЕ красный фломастер, это значит зеленый, синий, желтый или черный.
Всего их \( 3+2+2+1=8\). \( \displaystyle <
Так мы учились считать раньше, но сейчас, зная что такое полная вероятность, можно поступить немного проще.
Таким образом, вероятность вытащить НЕ красный фломастер – \( \displaystyle 1-\frac<2><10>=0,8\).
Ответ: \( \displaystyle 0,8\)
Вероятность того, что событие НЕ произойдет, равна \( \displaystyle 1\) минус вероятность того, что событие произойдет.
Правило умножения вероятностей независимых событий
Что такое независимые события ты уже знаешь.
А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?
Можно конечно посчитать, но есть способ проще.
Допустим мы хотим знать, какова вероятность того, что бросая монетку \( 2\) раза, мы два раза увидим орла?
Мы уже считали: \( p=0,25\).
А если бросаем монетку \( 3\) раза? Какова вероятность увидеть орла \( 3\) раза подряд?
Всего возможных вариантов \( 8\):
Не знаю, как ты, но я \( 3\) раза ошибся, составляя этот список. Ух! А подходит нам только \( 1\) вариант (первый).
Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.
Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.
Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий
Рассмотрим на примере все той же, злосчастной, монетки.
Вероятность выпадения орла в \( 1\) испытании? \( \displaystyle \frac<1><2>\). Теперь мы бросаем монетку \( 5\) раз.
Какова вероятность выпадения \( 5\) раз подряд орла?
Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.
Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при \( 3\) бросках подряд, мы поступили бы также.
Вероятность выпадения решка – \( \displaystyle \frac<1><2>\), орла – \( \displaystyle \frac<1><2>\).
Вероятность выпадения последовательности РЕШКА-ОРЕЛ-РЕШКА-РЕШКА:
Можешь проверить сам, составив таблицу.
Примеры:
Решения:
Правило сложения вероятностей несовместных событий
Так стоп! Новое определение.
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.
Ряд несовместных событий образуют полную группу событий.
Давай разбираться. Возьмем нашу изношенную монетку и бросим её \( 3\) раза. Возможные варианты:
Так вот, несовместные события – это определенная, заданная последовательность событий. \( 1),\text< >2),\text< >3),\text< >4)\ldots \text< >8)\) – это несовместные события.
Вероятности несовместных событий складываются.
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности \( 1\)) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно \( 1\) раз, т.е. варианты \( 4),\text< >6)\) и \( 7)\), то мы должны сложить вероятности этих последовательностей.
Всего вариантов \( 8\), нам подходит \( 3\).
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Правило, помогающее не запутаться, когда умножать, а когда складывать:
Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.
Возвратимся к примеру, когда мы подбросили монетку \( 3\) раза, и хотим узнать вероятность увидеть орла \( 1\) раз.
Что должно произойти?
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
\( \displaystyle \left( \frac<1><2>\cdot \frac<1><2>\cdot \frac<1> <2>\right)+\left( \frac<1><2>\cdot \frac<1><2>\cdot \frac<1> <2>\right)+\left( \frac<1><2>\cdot \frac<1><2>\cdot \frac<1> <2>\right)=\frac<1><8>+\frac<1><8>+\frac<1><8>=\frac<3><8>\)
Давай рассмотрим несколько примеров.
Пример 8
В коробке лежит \( 16\) карандашей. \( 2\) красных, \( 4\) зеленых, \( 5\) оранжевых и \( 3\) желтых и \( 2\) черных.
Какова вероятность вытащить красный или зеленый карандаши?
Решение:
Что должно произойти? Мы должны вытащить (красный ИЛИ зеленый).
Теперь понятно, складываем вероятности этих событий:
Ответ: \( \displaystyle 0,375\)
Пример 9
Игральную кость бросают дважды, какова вероятность того, что в сумме выпадет 8 очков?
Решение.
Как мы можем получить \( 8\) очков?
(\( 6\) и \( 2\)) или (\( 5\) и \( 3\)) или (\( 4\) и \( 4\)) или (\( 3\) и \( 5\)) или (\( 2\) и \( 6\)).
Вероятность выпадения одной (любой) грани – \( \displaystyle p=\frac<1><6>\).
Ответ: \( \displaystyle \frac<5><36>\)
Тренировка
Думаю, теперь тебе стало понятно, когда нужно как считать вероятности, когда их складывать, а когда умножать. Не так ли? Давай немного потренируемся.
Примеры:
Возьмем карточную колоду, в которой \( 52\) карты, из них \( 13\) пик, \( 13\) червей, 13 треф и 13 бубен. От \( 2\) до туза каждой масти.
Ответы:
Приме 11. \( \displaystyle p=\frac<13><52>\cdot \frac<13><52>=\frac<1><4>\cdot \frac<1><4>=\frac<1><16>=0,0625\)
Пример 12. \( \displaystyle p=\frac<13><52>+\frac<13><52>=\frac<1><4>+\frac<1><4>=\frac<1><2>=0,5\)
Пример 13. В колоде \( 4\) карты каждого достоинства, значит: \( \displaystyle p=\frac<4><52>+\frac<4><52>+\frac<4><52>+\frac<4><52>=\frac<16><52>=\frac<4><13>\)њ
Пример 14. События зависимы, так как после первой вытащенной карты количество карт в колоде уменьшилось (как и количество «картинок»).
Всего вальтов, дам, королей и тузов в колоде изначально \( 16
\left( 4+4+4+4 \right)\), а значит вероятность первой картой вытащить «картинку»:
Поскольку мы убираем из колоды первую карту, то значит в колоде осталось уже \( 51\) карта, из них \( 15\) картинок. Вероятность второй картой вытащить картинку:
Поскольку нас интересует ситуация, когда мы достаем из колоды: «картинку» И «картинку», то нужно перемножать вероятности:
Ответ: \( \displaystyle \frac<20><221>\)
Пример 15. После первой вытащенной карты, количество карт в колоде уменьшится.Таким образом, нам подходит два варианта:
Не забываем про уменьшение количества карт в колоде! \( \displaystyle p=\frac<4><52>\cdot \frac<12><51>+\frac<12><52>\cdot \frac<4><51>=\frac<12><13\cdot 51>+\frac<12><13\cdot 51>=\frac<24><663>=\frac<8><221>\)
Если ты смог сам решить все задачи, то ты большой молодец! Теперь задачи на теорию вероятностей в ЕГЭ ты будешь щелкать как орешки!
Задачи смешанного типа
Пример 16.
Монетку бросают два раза. Какова вероятность того, что результат бросков будет разный?
Решение.
Имеется в виду, что если первым выпал орел, второй должна быть решка, и наоборот. Получается, что здесь две пары независимых событий, и эти пары друг с другом несовместны. Как бы не запутаться, где умножать, а где складывать.
Есть простое правило для таких ситуаций.
Попробуй описать, что должно произойти, соединяя события союзами «И» или «ИЛИ».
Например, в данном случае:
Должны выпасть (орел и решка) или (решка и орел).
Там где стоит союз «и», будет умножение, а там где «или» – сложение:
Попробуй сам:
Решения:
Пример 17. (Выпал орел и выпал орел) или (выпала решка и выпала решка): \( p=\left( \frac<1><2>\cdot \frac<1> <2>\right)+\left( \frac<1><2>\cdot \frac<1> <2>\right)=\frac<1><4>+\frac<1><4>=\frac<1><2>=0,5\).
Пример 18. Какие есть варианты? \( 6+4,\text< >5+5\) и \( 4+6\). Тогда:
Выпало (\( 4\) и \( 6\)) или (\( 5\) и \( 5\)) или (\( 6\) и \( 4\)): \( p=\left( \frac<1><6>\cdot \frac<1> <6>\right)+\left( \frac<1><6>\cdot \frac<1> <6>\right)+\left( \frac<1><6>\cdot \frac<1> <6>\right)=\frac<1><36>+\frac<1><36>+\frac<1><36>=\frac<3><36>=\frac<1><12>\).
Пример 19. Ой, как же не хочется перебирать варианты… Орел-решка-решка, Орел-орел-решка, … А и не надо! Вспоминаем про полную вероятность. Вспомнил? Какова вероятность, что орел не выпадет ни разу?
Это же просто: все время летят решки, значит
Бонус: Вебинары из нашего курса подготовки к ЕГЭ
Теория вероятности. ЕГЭ №4 (54 задачи)
Что вы узнаете на этом уроке?
80% урока — решение задач
Математическая статистика
Мы вам рекомендуем также ознакомиться с нашей статьей по родственной теме — математическая статистика.
В статье вы найдете основные определения математической статистики и способы графического изображения данных.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Слово самому лучшему — тебе!
Сегодня ты узнал много нового! И теперь ты можешь решить любую задачу по теории вероятностей. Главное – сосредоточься и пойми, что к чему. Ты справишься!
А теперь мы хотим узнать твое мнение. Напиши нам в комментариях ниже!
Понравилась ли тебе статья? Какая задача показалась тебя самой сложной? Разобрался ли ты с ней?
Если у тебя остались вопросы, то не стесняйся спрашивать! Там же, в комментариях. Мы обязательно тебе ответим.
Добавить комментарий Отменить ответ
3 комментария
все очень супер понятно. Спасибо! удачи!
Спасибо, Nadzey! И вам удачи!
Руслан
13 марта 2020
Здравствуйте. Разъясните пожалуйста, казалось бы простую вещь. В коробке бесконечное множество карандашей, половина красные, половина зеленые. Не будем считать что карандаши убавляются, то есть события в принципе не зависимые. Если я достал по очереди три красных карандаша, то какова вероятность что я достану четвертый карандаш тоже красным. 50%?
Алексей Шевчук
20 марта 2020
Руслан, верно, 50%. Как с монеткой, один в один.
Александр
02 июля 2020
Если предположить, что задача решается, как с монеткой, то речь идет о выпадении четвертого раза одного из двух вариантов подряд, нет? То есть вероятность вытащить красный карандаш, как описано в примере выше — 50%, вытащить второй раз подряд красный карандаш — 25%, вытащить третий раз подряд красный карандаш — 12,5%. соответственно вероятность вытащить четвертый раз подряд красный карандаш — 6,25%, нет? P.S. С бесконечными карандашами странная аналогия — проще представить казино — красное и черное) Какова вероятность в казино, поставив четыре раза подряд на красное — выиграть?)
Алексей Шевчук
07 июля 2020
Ваши расчёты (6,25%) — это решение другой задачи: какова вероятность вытянуть 4 красных карандаша подряд, если мы пока что ещё ничего не вытаскивали. Но если мы знаем на 100%, что первыми тремя вытащим именно красные, наши расчёты ведь изменятся, верно? Аналогия с бесконечными карандашами вполне нормальная, это же просто математическая модель. Если хотите, можно просто каждый взятый караднаш возвращать обратно в коробку, чтобы их снова становилось поровну.
Алексей Шевчук
07 июля 2020
А с казино ситуация действительно очень похожая, за исключением одного маленького нюанса — сектора зеро. В рулетке 18 красных, 18 чёрных секторов, и один зеро — следовательно, вероятность выпадения красного не 1/2, а 18/37. Это нужно обязательно учитывать при расчёте вероятностей. Например, благодаря зеро не работает популярная когда-то стратегия: ставим рубль на красное, если он выпадает, забираем выигрыш, если нет, то удваиваем ставку. Теперь если выиграем, казино нам даст 2 рубля, что покроет предыдущий проигрыш и даст «заработок» в 1 рубль. Если снова не повезло — снова удваиваем ставку, таким образом, покрывая все прошлые проигрыши. Как только выиграли, возвращаемся к начальной ставке в 1 рубль. Весь расчёт здесь строится на том, что вероятность выиграть, умноженная на размер выигрыша, равна нашей ставке, поэтому мы как минимум ничего не теряем, а если вовремя остановиться, то и выигрываем. Но это не так (казино и рулетку не дураки придумали): именно благодаря зеро вероятность чуть меньше 1/2, но выигрыш всё равно в 2 раза больше ставки. Поэтому, играя много игр, мы проигрываем в среднем 1/37 поставленных денег — недостаточно много, чтобы мы что-то заподозрили, но достаточно, чтобы казино осталось в плюсе) Хорошо, что есть математика, и мы можем всё заранее расчитать, правда?
Александр (админ)
07 июля 2020
С казино стратегия удвоения не работает не только по причине зеро. В каждом казино есть минимальный и максимальный размер ставки и поэтому удваивать получится не больше 4-5 раз. Рано или поздно игрок проиграет все, если будет придерживаться этой стратегии.