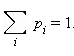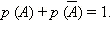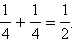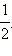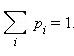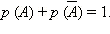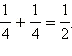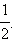Бросают кубик элементарными являются события что
Бросают кубик элементарными являются события что
В нашем случае события образуют множество элементарных событий. Для них верно 
К классу возможных событий относятся все подмножества множества элементарных событий. Например, при броске «выпало 1 или 2», «выпало 3» и т. д.
Сумма вероятностей события и его отрицания есть достоверное событие, то есть 
Несовместными называются события, которые не могут произойти одновременно. Например, события 1 и 2 являются несовместными: на кубике не могут одновременно выпасть 1 и 2.
Выпишем все возможные результаты броска кубика : 1, 2, 3, 4, 5, 6. Действительно, вариантов с выпадением 1 или 5 два, всего вариантов шесть, получаем
При бросании кубика может наступить 6 различных исходов, а при бросании кубика – тоже 6. Из комбинаторики мы знаем, что количество вариантов, возникающих при бросании двух кубиков (, и так далее), равно произведению количества исходов для кубиков в отдельности, то есть 6 ∙ 6 = 36. Поскольку все такие исходы равновероятны, то каждый из них может наступить с вероятностью 1/36.
К каким классам событий (возможное, невозможное, достоверное) относятся: а) расстояние между двумя произвольными городами меньше, чем 50 тысяч километров; б) наугад выбранное слово русского языка заканчивается буквами «нзо»; в) Вася выиграет в лотерее?
Первое из событий достоверное, а второе – невозможное. Третье событие может произойти, а может не произойти – оно является возможным, но не достоверным.
Укажите события, противоположные данным: а) на кубике выпало 1; б) Света получила на экзамене «5»; в) после ночи наступает утро?
а) На кубике не выпало 1; б) Света не получила на экзамене «5» (в том случае, если Света сдавала экзамен, то можно утверждать, что Света получила какую-то другую оценку); в) после ночи не наступает утро. Заметим, что событие, противоположное событию в) является невозможным (во всяком случае, в нашей обыденной жизни).
Совместны ли события: а) на первом кубике выпало 1, а на втором – 2; б) Юра пошёл в школу, а завтра будет дождь; в) Иванов в настоящее время является президентом страны, и Петров является президентом той же страны.
Пара событий из примера а) совместна, так как может произойти одновременно. Точно так же совместна и пара событий б). Пара событий в) несовместна, так как не может произойти одновременно.
Уточним понятие независимых событий. Будем бросать две монеты и обозначим как событие тот факт, что первая монета упадет гербом, событие – вторая монета упадет гербом, событие – на одной (и только на одной) монете выпадет герб. (Пример взят из книги Г. Секея «Парадоксы в теории вероятностей и математической статистике».) Тогда события попарно независимы, но два из них полностью определяют третье. Действительно, независимы, так как результаты второго броска никак не зависят от первого броска, (а также ) могут показаться зависимыми, но перебором вариантов можно получить, что значит, они по определению независимые. С другой стороны, легко убедиться, что любые два события однозначно определяют третье. На этом примере хорошо видно, что события могут быть попарно независимы, но зависимы в совокупности.
Теперь, ознакомившись с языком теории вероятностей, мы можем дать более строгое определение вероятности и выписать основные её свойства.
Вероятностью события называется некоторая действительная функция, определённая на классе возможных событий и удовлетворяющая следующим трём аксиомам, сформулированным А. Н. Колмогоровым.
Из перечисленных аксиом можно вывести следующие свойства вероятностей.
Пассажир ждёт трамвая № 2 или № 7 возле остановки, на которой останавливаются трамваи № 2, № 5, № 7 и № 24. Считая, что трамваи всех маршрутов появляются случайным образом (не по расписанию) одинаково часто, найдите вероятность того, что первый подошедший к остановке трамвай будет нужного пассажиру маршрута.
Ясно, что вероятность того, что первым подойдёт трамвай № 2, равна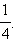 
Такова же вероятность, что первым подойдёт трамвай № 7. Искомая вероятность, следовательно, равна 
Ответ. 
Пусть для некоторого стрелка вероятность попадания в область 1 мишени, изображённой на рисунке, равна 0,25, а вероятность попадания в область 2 – 0,15. Какова вероятность того, что стрелок попадёт либо в область 1, либо в область 2?
По правилу сложения вероятностей получаем, что искомая вероятность
Бросают кубик элементарными являются события что
В нашем случае события образуют множество элементарных событий. Для них верно 
К классу возможных событий относятся все подмножества множества элементарных событий. Например, при броске «выпало 1 или 2», «выпало 3» и т. д.
Сумма вероятностей события и его отрицания есть достоверное событие, то есть 
Несовместными называются события, которые не могут произойти одновременно. Например, события 1 и 2 являются несовместными: на кубике не могут одновременно выпасть 1 и 2.
Выпишем все возможные результаты броска кубика : 1, 2, 3, 4, 5, 6. Действительно, вариантов с выпадением 1 или 5 два, всего вариантов шесть, получаем
При бросании кубика может наступить 6 различных исходов, а при бросании кубика – тоже 6. Из комбинаторики мы знаем, что количество вариантов, возникающих при бросании двух кубиков (, и так далее), равно произведению количества исходов для кубиков в отдельности, то есть 6 ∙ 6 = 36. Поскольку все такие исходы равновероятны, то каждый из них может наступить с вероятностью 1/36.
К каким классам событий (возможное, невозможное, достоверное) относятся: а) расстояние между двумя произвольными городами меньше, чем 50 тысяч километров; б) наугад выбранное слово русского языка заканчивается буквами «нзо»; в) Вася выиграет в лотерее?
Первое из событий достоверное, а второе – невозможное. Третье событие может произойти, а может не произойти – оно является возможным, но не достоверным.
Укажите события, противоположные данным: а) на кубике выпало 1; б) Света получила на экзамене «5»; в) после ночи наступает утро?
а) На кубике не выпало 1; б) Света не получила на экзамене «5» (в том случае, если Света сдавала экзамен, то можно утверждать, что Света получила какую-то другую оценку); в) после ночи не наступает утро. Заметим, что событие, противоположное событию в) является невозможным (во всяком случае, в нашей обыденной жизни).
Совместны ли события: а) на первом кубике выпало 1, а на втором – 2; б) Юра пошёл в школу, а завтра будет дождь; в) Иванов в настоящее время является президентом страны, и Петров является президентом той же страны.
Пара событий из примера а) совместна, так как может произойти одновременно. Точно так же совместна и пара событий б). Пара событий в) несовместна, так как не может произойти одновременно.
Уточним понятие независимых событий. Будем бросать две монеты и обозначим как событие тот факт, что первая монета упадет гербом, событие – вторая монета упадет гербом, событие – на одной (и только на одной) монете выпадет герб. (Пример взят из книги Г. Секея «Парадоксы в теории вероятностей и математической статистике».) Тогда события попарно независимы, но два из них полностью определяют третье. Действительно, независимы, так как результаты второго броска никак не зависят от первого броска, (а также ) могут показаться зависимыми, но перебором вариантов можно получить, что значит, они по определению независимые. С другой стороны, легко убедиться, что любые два события однозначно определяют третье. На этом примере хорошо видно, что события могут быть попарно независимы, но зависимы в совокупности.
Теперь, ознакомившись с языком теории вероятностей, мы можем дать более строгое определение вероятности и выписать основные её свойства.
Вероятностью события называется некоторая действительная функция, определённая на классе возможных событий и удовлетворяющая следующим трём аксиомам, сформулированным А. Н. Колмогоровым.
Из перечисленных аксиом можно вывести следующие свойства вероятностей.
Пассажир ждёт трамвая № 2 или № 7 возле остановки, на которой останавливаются трамваи № 2, № 5, № 7 и № 24. Считая, что трамваи всех маршрутов появляются случайным образом (не по расписанию) одинаково часто, найдите вероятность того, что первый подошедший к остановке трамвай будет нужного пассажиру маршрута.
Ясно, что вероятность того, что первым подойдёт трамвай № 2, равна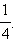 
Такова же вероятность, что первым подойдёт трамвай № 7. Искомая вероятность, следовательно, равна 
Ответ. 
Пусть для некоторого стрелка вероятность попадания в область 1 мишени, изображённой на рисунке, равна 0,25, а вероятность попадания в область 2 – 0,15. Какова вероятность того, что стрелок попадёт либо в область 1, либо в область 2?
По правилу сложения вероятностей получаем, что искомая вероятность
Классическое определение вероятности события
Основные понятия теории вероятностей
Испытание и событие
Испытание (опыт, эксперимент) – это выполнение определенных условий, при которых наблюдается изучаемое явление.
Стрельба по мишени, бросание монеты, вынимание шаров из урны – это все примеры опытов.
Событие – это результат опыта. Будем обозначать события латинскими буквами 
, 
, 
, …
Пример 1.Производитсявыстрел по мишени.Событие — попадание в мишень, событие — промах.
Пример 2.Бросают монету. Событие — выпал герб, событие 
— выпало число.
Пример 3. В урне находятся черные и белые шары. Из урны извлекают один шар. Событие 
— извлечен черный шар, событие 
— извлечен белый шар.
Пример 4.Бросают кубик. Событие 
— выпало число 1, событие 
— выпало число 2.
Достоверное, невозможное и случайное события
Событие называется достоверным, если оно обязательно произойдет в результате опыта.
Пример 5. В урне находятся только черные шары. Из урны извлекают один шар. Событие 
— «извлечен черный шар» является достоверным, так как всегда вынимают черный шар.
Пример 6. Бросают кубик. Событие 
— «выпало какое-то число от 1 до 6» является достоверным.
Событие называется невозможным, если оно не может произойти в данном испытании.
Пример 7. В урне находятся только черные шары. Из урны извлекают один шар. Событие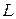 
— «извлечен белый шар» является невозможным.
Пример 8. Бросают кубик. Событие — «выпало число 7» является невозможным.
Событие называется случайным, если оно может произойти в данном опыте, а может и не произойти.
Пример 9.События и из примера 1, события и 
из примера 2, события и из примера 3, события и из примера 4 – это примеры случайных событий.
Совместные и несовместные события
Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого события.
Пример 10.Два стрелка делают по одному выстрелу в мишень. Событие — попадание 1-го стрелка в мишень и событие — попадание 2-го стрелка в мишень. Эти события совместные, так как возможна ситуация, когда оба стрелка попадут в мишень.
Два события называются несовместными в данном опыте, если появление одного из них е исключает появление другого события.
Пример 11.События и из примера 1, события и из примера 2, события и из примера 3, события и из примера 4 – это примеры несовместных событий.
Полная группа событий
Множество событий называется полной группой событий, если они попарно несовместны (то есть никакие два из них не могут произойти одновременно) и какое-то из них обязательно произойдет.
Противоположные события – это полная группа из двух событий. Одно из противоположных событий обозначается буквой, а другой – той же буквой с чертой ( и 
).
Пример 12. События и из примера 2 – противоположные: 
, или 
.
Пример 13.Бросают кубик. Событие 
— выпало число 
( = 1, 2, 3, 4, 5, 6). Эти 6 событий образуют полную группу событий, так как всегда выпадает какое-то число от 1 до 6 и невозможна ситуация, когда при одном бросании выпадают сразу два числа.
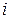
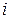
Операции над событиями
Сумма событий
Суммой 
событий и 
называется событие, состоящее в появлении хотя бы одного из них, то есть могут появиться либо только событие , либо только событие , либо оба события и одновременно.
 |
На рисунке множества 
отождествляются с событиями 
. Заштрихованное множество включает в себя точки, входящих в область или в область , то есть объединение областей 
. Этому множеству соответствует событие .
Пример 14.Два стрелка делают по одному выстрелу в мишень. Событие — попадание 1-го стрелка в мишень и событие — попадание 2-го стрелка в мишень. Сумма событий – это попадание в мишень хотя бы одного из этих стрелков.
Пример 15. Из урны, в которой находятся черные и белые шары, вынимают два шара. Событие — 1-й вынутый шар черный, событие — 2-й вынутый шар черный. Тогда сумма 
событий – это появление хотя бы одного черного шара.
Произведение событий
Произведением 
событий и называется событие, состоящее в их одновременном появлении.
 |
Заштрихованное множество есть общая часть областей 
и . Это соответствует тому, что произошли одновременно все события и , т.е. 
.
Пример 16. В примере 14 произведение 
событий — попадание 1-го стрелка в мишень и — попадание 2-го стрелка в мишень – это попадание в мишень обоих стрелков.
Пример 17.В примере 15 произведение 
событий — 1-й вынутый шар черный, событие — 2-й вынутый шар черный – это то, что оба вынутых шара будут черного цвета.
Сложные события
Пример 18. По мишени производится два выстрела. Событие 
— попадание в мишень при -ом выстреле ( = 1,2). Пользуясь операциями над событиями, запишите события: – два попадания, – два промаха, – только одно попадание, 
– хотя бы одно попадание, 
– ни одного попадания.
— два попадания; 
– два промаха;
— только одно попадание;
– хотя бы одно попадание;
— ни одного попадания.
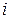
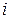
Вероятность события
Элементарные исходы
События называются равновозможными, если нет оснований считать, что одно из них происходит чаще других.
Каждое равновозможное событие, которое может произойти в данном опыте, называется элементарным исходом.
Пример 19. События из примера 13 – равновозможные события. — элементарные исходы ( = 1, 2, 3, 4, 5, 6). События и из примера 2 – равновозможные события. и 
— элементарные исходы.
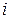
Множество 
всех равновозможных элементарных исходов испытания называется пространством элементарных исходов (событий) испытания.
Пример 20.События — выпало число ( = 1, 2, 3, 4, 5, 6) образуют пространство элементарных событий испытания «бросание кубика».
Элементарные исходы, при которых наступает некоторое событие, называются элементарными исходами, благоприятствующими этому событию.
Пример 23.В примере 13событию — «выпало четное число очков» благоприятствуют выпадение 2, 4 или 6 (то есть элементарные исходы , = 2, 4, 6). Событию — «выпало простое число» благоприятствуют выпадение 2, 3 или 5 (то есть элементарные исходы , = 2, 3, 5).
Классическое определение вероятности события
Вероятностью события называется отношение числа исходов 
, благоприятствующих событию , к числу 
всех равновозможных исходов опыта: 
.
Пример 24.Бросают кубик. Событие — выпало число ( = 1, 2, 3, 4, 5, 6). Событию «выпало четное число очков» благоприятствуют 
три элементарных исхода, а всего возможно 
элементарных исходов. Следовательно, вероятность события равна 
.
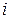
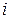
Пример 25. При бросании монеты 
(выпал герб) = (выпало число)= 0,5.
Свойства вероятности
1. Вероятность достоверного события равна 1.
2. Вероятность невозможного события равна 0.
3. Вероятность случайного события есть положительное число, заключенное между 0 и 1, то есть 
.
1. Приведите пример опыта (испытания), который можно повторить достаточно много раз, но результат нельзя предсказать заранее. Укажите его закономерности.
2. Приведите примеры пространства элементарных событий.
3. Дайте определения понятиям: событие, достоверное событие, невозможное событие, противоположное событие. Приведите примеры.
4. Назовите противоположные события для событий:
— попадание в мишень при первом из трех выстрелов;
— выпадение четного числа очков при подбрасывании игрального кубика;
— хотя бы один раз выпал герб;
— из двух стрелков оба стрелка не попали.
5. Какое событие называется суммой событий? Приведите пример.
6. Какое событие называется произведением событий?Приведите
пример.
7. Пусть , , — события, наблюдаемые в одном и том же эксперименте. Опишите события: 1) + + ; 2) ; 3) 
+ 
+ 
; 4) 
; 5) 
.
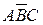
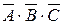
8. Какие элементарные события называются благоприятствующими событию в данном опыте? Приведите пример.
9. Что называется вероятностью события?
10. Дайте классическое определение вероятности события. Укажите, при каких условиях оно применимо.
11. Чему равны вероятности достоверного события, невозможного события, случайного события?