Броуновское движение частиц в воде объясняется тем что

Броуновское движение

Всего получено оценок: 152.

Всего получено оценок: 152.

Броуновское движение – хаотичное движение мельчайших видимых частиц твердого вещества в газе или жидкости. Так в чем суть, и чем обусловлено броуновское движение частиц?

Открытие броуновского движения

В 1827 году ботаник Роберт Броун наблюдал за движением пыльцевых зерен в жидкости. Он обнаружил, что эти мельчайшие частицы безостановочно и хаотично движутся в воде. Этот случай его очень удивил, первой его реакцией было высказывание о том, что, наверное, пыльца живая, раз может двигаться. Поэтому тот же опыт он проделал с неорганическими веществами. И уже на основе этого примера выяснил, что частицы определенных размеров, независимо от того, органические они или неорганические, движутся хаотично и безостановочно в жидкостях и газе.

Уже позже было установлено, что в зависимости от размера частицы участвуют или не участвуют в броуновском движении. Если размер частицы более 5 мкм, то эти частицы в броуновском движении практически не участвуют. Если размер частиц менее 3 мкм, то эти частицы движутся хаотично, поступательно, либо вращаются.

Броуновские частицы в водной среде обычно не тонут, но и не всплывают на поверхность. Они находятся в толще жидкости во взвешенном состоянии

Уже в XIX веке броуновское движение изучал французский физик Луи Жорж Гуи. Он установил, что чем меньше внутреннее трение жидкости, тем броуновское движение становится интенсивнее.

Рис. 2. Портрет Луи Жорж Гуи.

Броуновское движение не зависит от освещения и внешнего электромагнитного поля. Оно вызвано влиянием теплового движения молекул.

Общая характеристика броуновского движения

Броуновское движение имеет место быть, так как все жидкости и газы состоят из атомов и молекул, которые постоянно находятся в движении. Следовательно, броуновская частица, попадая в жидкую или газообразную среду, подвергается воздействию этих атомов и молекул, которые двигают и толкают ее.

Когда в жидкую или газообразную среду помещено крупное тело, то толчки формируют постоянное давление. Если же среда окружает крупное тело со всех сторон, то давление уравновешивается, и на тело действует только сила Архимеда. Такое тело либо всплывает, либо тонет.

Рис. 3. Броуновское движение пример.

Броуновское движение объясняется тем, что благодаря случайной неодинаковости количества ударов молекул жидкости о частицу с разных направлений возникает равнодействующая сила определенного направления.

Что мы узнали?

Броуновское движение – бесконечное и хаотичное движение частиц определенного размера в газе или жидкости, молекулы и атомы которых приводят в движение эти частицы. В данной статье дается определение броуновского движения, а также объясняются причины его возникновения.

Источник

Физика. 7 класс

Соль или сахар в горячей воде растворяется быстрее, чем в холодной, потому что:

молекулы холодной воды с трудом разрушают пространственную решетку кристалла

процесс диффузии с ростом температуры ускоряется

молекулы холодной воды сильнее препятствуют движению молекул растворяемого вещества, чем молекулы горячей воды

Броуновское движение частиц в воде объясняется тем, что:

броуновские частицы подвергаются «бомбардировке» со стороны хаотично движущихся молекул

броуновские частицы представляют собой живые клетки, движущиеся в воде

молекулы воды подвергаются «бомбардировке» со стороны хаотично движущихся броуновских частиц

Диффузия протекает быстрее всего:

во всех веществах одинаково

Впишите в текст пропущенные слова.

Два куска мела не соединяются вместе даже при сильном сжатии, а два куска пластилина легко соединяются при незначительном сдавливании, потому что:

молекулы пластичных веществ удаётся без труда сблизить на расстояние, на котором начинают проявляться силы межмолекулярного притяжения

у твёрдых тел отталкивание между молекулами всегда преобладает над притяжением

у пластичных и легкодеформируемых тел притяжение между молекулами всегда преобладает над отталкиванием

Как из нескольких сортов фильтровальной бумаги выбрать тот, в котором поры меньше, не используя при этом никаких приборов?

Конец полоски бумаги опускаем в воду: в бумаге с меньшими порами вода поднимется на меньшую высоту

Менее шероховатая бумага обладает меньшими порами

Концы полосок разных сортов бумаги опускаем в воду: в той полоске, где поры меньше, вода поднимется на большую высоту

Если положить мел на мокрую губку, то он намокнет. Если же сухую губку положить на мокрый мел, то она останется сухой, потому что:

у мела капилляры меньше, чем у губки

молекулы воды в губке обладают большей подвижностью, чем молекулы воды в мокром меле

когда мел находится на губке, то расстояния между молекулами мела и воды становятся меньше, и мел намокает

Источник

Диффузия, растворимость и броуновское движение могут быть объяснены только на основе представления о молекулярном строении веществ и являются убедительными обоснованиями пер­вого и второго положений молекулярно-кинетической теории.

Броуновское движение.

Броуновское движение (брауновское движение) — беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды.

Впервые такое движение исследовал и описал в 1827 г. английский ботаник Р. Браун при изуении под микроскопом взвешенной в воде цветочной пыльцы. Он обнаружил, что частички пыль­цы находятся в непрерывном беспорядочном движении, как бы исполняя дикий фантастический танец. Он писал: «Это движение, как я убежден, обусловлено не потоками жидкости, не постепен­ным ее испарением, а принадлежит самим частицам».

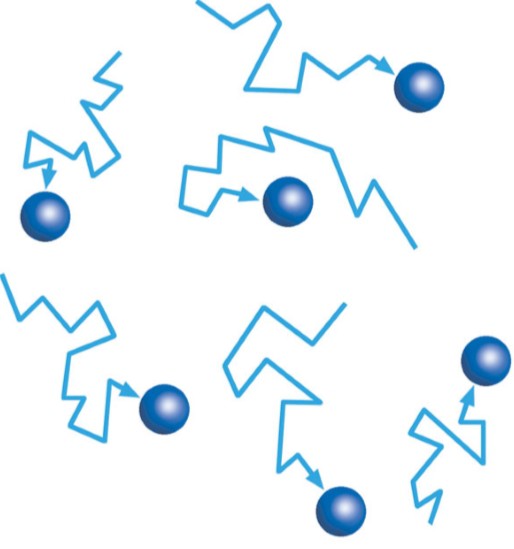
Наблюдаемые (броуновские) частицы размером

1 мкм и менее совершают неупорядоченные независимые движения, описывая слож­ные зигзагообразные траектории.

Подобный опыт можно проделать, пользуясь краской или тушью, предварительно растертой до таких мельчайших крупинок, которые видны лишь в микроскоп. Можно увидеть, что крупинки краски не­прерывно движутся. Самые мелкие из них беспорядочно перемещают­ся с одного места в другое, более крупные лишь беспорядочно колеб­лются.

Броуновское движение можно наблюдать и в газе. Например, в воздухе его совершают взвешенные там частицы пыли или дыма.

Броуновское движение никогда не прекращается! В капле воды (если не давать ей высохнуть) движение крупинок можно наблюдать в течение многих дней, месяцев, лет. Оно не прекращается ни ле­том, ни зимой, ни днем, ни ночью. В кусках кварца, пролежавших в земле тысячи лет, попадаются иногда капельки воды, замурованные в минерале. В этих капельках тоже наблюдали броуновское движение плавающих в воде частиц.

Интенсивность броуновского движения увеличивается с повыше­нием температуры, уменьшением вязкости среды, уменьшением размера частиц. Оно не зависит от химической природы частиц и време­ни наблюдения.

Броуновское движение служит доказательством существования еще более мелких частиц — молекул жидкости, невидимых даже в самые сильные оптические микроскопы.

Броуновское движение объясняется тем, что благодаря случайной неодинаковости количества ударов молекул жидкости о частицу с разных направлений возникает равнодействующая сила определенного направления. Поскольку подобные флуктуации (флуктуа­ция — случайное отклонение физической величины от ее среднего значения) очень кратковременны, то в следующий миг направление равнодействующей меняется и, следовательно, изменится направление перемещения частицы. Отсюда наблюдающаяся хаотичность броуновского движения, которая отражает хаотичность молекулярного движения.

Открытие броуновского движения имело большое значение для изучения строения вещества. Оно показало, что тела действительно состоят из отдельных частиц — молекул — и что молекулы находятся в непрерывном беспорядочном движении.

Полная теория броуновского движения была разработана Эйнштейном и Смолуховским в 1905-1906 гг. и экспериментально подтверждена Ж. Перреном. Выводы теории показали, что среднее значение квадрата смещения броуновской частицы за определенный промежуток времени про­порционально этому промежутку времени, температуре и постоянной Больцмана.

Эксперименты Ж. Перрена, в которых он определял положение одной определенной части­цы через каждые 30 с, подтвердили выводы теории. Перрен проводил также опыты по проверке зависимости концентрации молекул газа от высоты и барометрической формулы — зависимости атмосферного давления от высоты. Он предположил, что броуновские частицы, являясь своего рода большими молекулами, должны подчиняться тем же законам, что и молекулы атмосферы, а, следовательно, их концентрация с высотой должна падать. Его эксперименты полностью подтвердили теорию. Они позволили ему определить постоянную Авогадро, значение которой совпало с уже известным.

Таким образом, броуновское движение является самым ярким подтверждением теплового движения молекул — одного из положений молекулярно-кинетической теории.

Диффузия.

Явление, при котором происходит взаимное проникновение молекул одного вещества между молекулами другого, называется диффузией.

Явление это объясняется свойством молекул находиться в беспрерывном движении.

Подтверждением движения молекул газа является всем известное распространение запаха какого-либо пахучего вещества, внесенного в комнату.

В жидкостях наблюдать взаимное проникновение одного вещества в другое можно, если в крепкий раствор медного купороса осторожно добавить воду. Вначале резкая граница между темно-голубым медным купоросом и бесцветной водой со временем исчезает. Механизм проникновения молекул следующий. Сначала вследствие движения отдельные молекулы воды и медного купороса, находящиеся около границы между ними, обмениваются местами. Молекулы медного купороса попадают в нижний слой воды, а молекулы воды — в верхний слой медного купороса. Граница между жидкостями из-за этого расплывается. Проникнув в слой «чужой» жидкости, молекулы начинают обмениваться местами с ее частицами, находящимся во все более глубоких слоях. Граница между жидкостями становится все более расплывчатой. Благодаря беспрерывно­му и беспорядочному движению молекул этот процесс, в конце концов, приводит к тому, что вся жидкость становится однородной.

В твердых телах также наблюдается диффузия. Так, в одном из опытов гладко отшлифованные пластины свинца и золота положили друг на друга и сжали грузом. Через пять лет золото и свинец проникли друг в друга на 1 мм.

Скорость диффузии зависит от агрегатного состояния вещества и температуры тела. В га­зах, где расстояние между молекулами очень велико по сравнению с их размерами и движение молекул хаотично, скорость диффузии наибольшая. В жидкостях она меньше, так как и расстояние между молекулами меньше, и движение молекул чуть более упорядочено. В твердых телах, где наблюдается строгий порядок в расположении атомов (или молекул), а сами они совершают лишь небольшие колебательные движения около своих мест, скорость диффузии наименьшая.

Скорость протекания диффузии увеличивается с ростом температуры.

Взаимодействие частиц вещества.

Третье положение MKT о взаимодействии молекул является очевидным. Достаточно вспомнить, сколько усилий требуется, чтобы сломать, скажем, деревянную палку.

Твердые тела и жидкости не распадаются на отдельные молекулы, несмотря на то, что их молекулы разделены промежутками и находятся в непрерывном беспорядочном движении.

Более того, твердое тело, например, трудно растянуть или сжать. Чем же объяснить, что молекулы в телах не только удерживаются друг около друга, но и в некоторых случаях промежутки между ними трудно увеличить?

Дело в том, что молекулы взаимодействуют друг с другом, и природа этого взаимодействия — электрическая. Молекула состоит из заряженных частиц — электронов и ядер. Заряженные частицы одной молекулы при соответствующих расстояниях взаимодействуют (притягиваются или отталкиваются) с заряженными частицами других молекул.

На расстояниях, превышающих 2-3 диаметра молекул, результирующая сила взаимодействия определяется силами притяжения. Вклад последних по мере уменьшения расстояния между молекулами сначала растет, затем убывает. Силы взаимодействия обращаются в нуль, когда расстоя­ние между молекулами становится равным сумме радиусов молекул.

Дальнейшее уменьшение расстояния приводит к перекрыванию электронных оболочек, что вызывает быстрое нарастание сил отталкивания.

Источник

Броуновское движение

Броуновское движение — это беспорядочные перемещения малых частиц, возникающие вследствие их столкновения с невидимыми молекулами воды или газа. Первым его обнаружил ботаник Роберт Броун — частицы пыльцы, которые он разглядывал под микроскопом на мокром предметном стекле, двигались рывками, — однако описать математически смог только Альберт Эйнштейн. Броуновское движение объясняет, как распространяется в спокойном воздухе пыльца, но и описывает также множество случайных процессов — от наводнений до скачков на фондовом рынке. Его непредсказуемые рывки связаны с фракталами.

В XIX веке ботаник Роберт Броун, разглядывая под микроскопом частицы пыльцы, обнаружил, что они не стоят на месте, но отрывисто двигаются. На миг он задумался — уж не живые ли они? Нет, конечно, просто их сбивали с места молекулы воды, которой Броун смачивал предметные стекла. Частицы пыльцы двигались хаотично, иногда лишь немного, иногда на довольно большие расстояния, и, в конечном счете, совершали по стеклу путь, предсказать который было невозможно. И многие ученые начали задумываться над открытием Броуна, названным в его честь «броуновским движением».

Случайное блуждание

Броуновское движение совершается любыми малыми частицами, находящимися во взвешенном состоянии в жидкости или газе. Его можно наблюдать даже у довольно больших частиц, например частиц дыма, — при большом увеличении видно, какие зигзаги они описывают в воздухе. Сила получаемых частицами ударов зависит от импульса молекул. Она оказывается большей в случае тяжелых молекул жидкости либо газа — как и в случае быстро движущихся, например, молекул нагретой жидкости.

Во второй половине XIX века предпринималась не одна попытка описать броуновское движение математически, однако сделать это смог лишь Эйнштейн в 1905 году, когда он также опубликовал специальную теорию относительности и дал описание фотоэффекта, за что получил Нобелевскую премию. Эйнштейн воспользовался тепловой теорией, основанной на столкновениях молекул, и успешно объяснил движения частиц, которые наблюдал Броун. Поняв, что броуновское движение доказывает существование молекул жидкостей, физики вынуждены были принять и учение об атомах, которое даже в начале XX века еще вызывало сомнения.

Диффузия

Со временем броуновское движение способно заставить частицу пройти значительное расстояние, хоть, разумеется, и не такое, какое она могла бы пройти, если бы никто не мешал ей двигаться по прямой. Это объясняется случайным характером движения молекул, которые с равной вероятностью могут толкать ее и вперед, и назад. Поэтому, если уронить в жидкость плотную группу частиц, они начнут рассеиваться (диффундировать) во все стороны даже при том, что жидкость никто не будет помешивать и никакие потоки в ней не возникнут. Каждая частица пойдет по своему пути, и капля начнет расширяться, образуя диффузное облако. Такое рассеяние играет важную роль в распространении загрязнений воздуха, имеющих точечный источник, например в распространении аэрозоля в атмосфере. Даже при полном отсутствии ветра химические вещества будут рассеиваться в воздухе вследствие одного лишь броуновского движения.

Фракталы

Путь, по которому следует частица, совершающая броуновское движение, дает нам пример фрактала. Каждый прямой отрезок этого пути может иметь любую длину и любое направление, однако некоторый общий рисунок все же существует. Этот рисунок несет в себе определенную структуру, в каком масштабе его ни разглядывай — от наименьшего из вообразимых до очень больших. А это и есть определяющее свойство фрактала.

Фракталы были в 1960-х и 1970-х предложены Бенуа Мандельбротом как метод представления самоподобных фигур в количественной форме. Фракталы — это фигуры, которые при любом масштабе выглядят одинаково. Если увеличить малый кусочек этой фигуры, вы увидите точно такую же, неотличимую от первой, рассматриваемой в большем масштабе, поэтому определить степень увеличения, глядя на фигуру, ни за что не удастся. Такая безмасштабная повторяемость часто встречается в природе — в рисунке береговой линии, в ветвях дерева, в листьях папоротника, в шестикратной симметрии снежинки.

Фракталы отличаются тем, что их длина или размерность не зависят от того, с каким увеличением вы их рассматриваете. Если вы решите измерить расстояние между двумя приморскими городами, Лендс-Эндом и Маунтс-Беем, то, скорее всего, придете к выводу, что оно составляет 30 км, однако вспомните про все береговые скалы и попробуйте обвить каждую веревкой — и вы обнаружите, что веревка вам понадобится в сотню километров длиной. Если же вы пойдете еще дальше и затеете обмерять каждую песчинку берега, веревку придется удлинить до многих сотен километров. Выходит, что абсолютная длина береговой линии зависит от масштаба, в котором вы проводите измерения. Ограничьтесь грубым очертанием берега — и вы снова вернетесь к уже знакомым вам 30 км. В этом смысле фрактальная размерность есть мера огрубления чего-то, будь то облако, дерево или горный хребет. Многие из фрактальных форм, например береговую линию, можно получить соединением шагов случайного движения — отсюда и их связь с броуновским движением.

Математика броуновского движения, или последовательность случайных шагов, может использоваться для создания фрактальных фигур, находящих применение во многих областях науки. С ее помощью можно создавать грубо очерченные виртуальные пейзажи — горы, деревья, облака — компьютерных игр, ее можно использовать в программах пространственного картирования, которые помогают роботам двигаться по сильно пересеченной местности, моделируя ее возвышенности и низины. Врачи применяют ее для медицинской визуализации, когда у них возникает нужда проанализировать структуру сложных органов тела, скажем легких, в которых ветвящиеся структуры присутствуют во всех масштабах, от грубого до совсем малого.

Идеи броуновского движения используются и для предсказания рисков либо событий будущего, которые являются суммарным результатом множества случайных воздействий — наводнений, колебаний фондового рынка. Фондовый рынок можно рассматривать как портфель ценных бумаг, стоимость которых варьируется случайным образом, напоминая броуновское движение множества молекул. Фигурирует оно и в моделировании других социальных процессов, относящихся к производству товаров и принятию решений. Броуновское движение с его случайным характером обладает значительным влиянием и появляется во множестве обличий — не в одном только танце чаинок в чашке горячего чая.

Источник

Броуновское движение

Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.

2. Броуновское движение

Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.

Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.

Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.

Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.

4. Свойства броуновского движения и диффузии

Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:

2) от рода вещества, в котором эти процессы происходят;

3) от агрегатного состояния.

То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.

5. Практическое применение

Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.

Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.

Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.

6. Методические рекомендации учителям

1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.

2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.

3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.

4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!

5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.

Источник