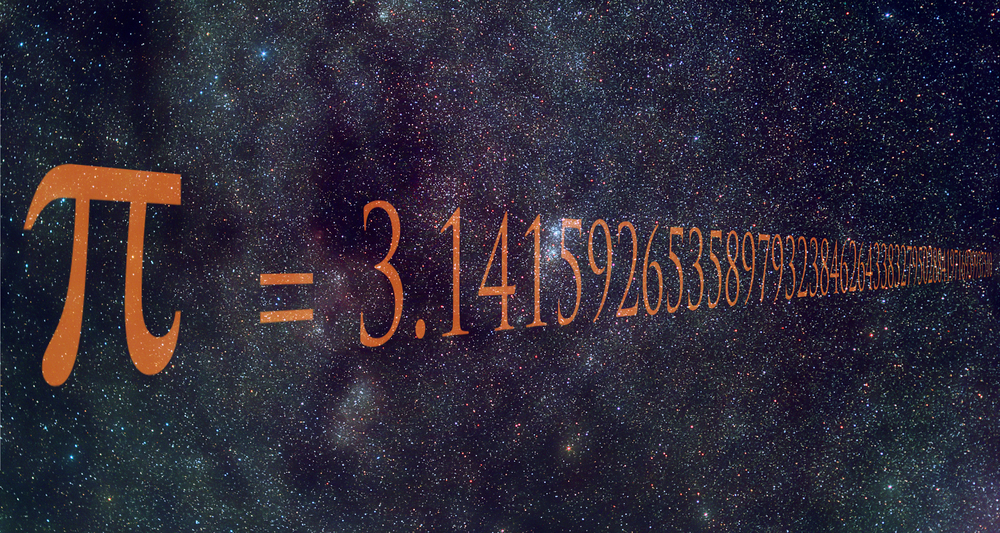Буква i в математике что это

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Число i

Лейб Штейнгарц,
доктор педагогики.
Иерусалим, Израиль
leybleyb@yahoo.com

НИ ЧИСЛО ПИ, НИ ЧИСЛО – НЕ ЯВЛЯЮТСЯ САМЫМИ ЛУЧШИМИ

На тему «КАКОЕ ЧИСЛО ЛУЧШЕ» уже были высказаны три различные точки зрения.

Первая: Число лучше, чем число Пи.

Вторая: Число Пи лучше, чем число .

Третья: Оба числа Пи и — одинаково хороши…

Но ведь споры часто длятся практически бесконечно.
Поэтому, в принципе, возможна и четвертая (и, видимо, далеко не последняя) точка зрения:

О ТОМ, ЧТО ОБА ЧИСЛА ПИ И — ОДИНАКОВО ПЛОХИ.

Вот, как нам кажется, могла бы быть обоснована эта позиция.
=============================================

Молодежная организация «МНИМАЯ СИЛА» абсолютно не согласна со всеми предыдущими мнениями.
И обращает внимание мировой общественности на приводимые ниже убедительные доводы.

Только мнимые числа, (а также и комплексные, которые возникли, безусловно, благодаря мнимым) могут претендовать на роль самых лучших чисел.

(1) В самой красивой математической формуле действительно присутствуют числа и . Но этой формулы вовсе бы не было без нашего замечательного числа .

(3) Число (“ай”) присутствует во многих фамилиях выдающихся деятелей искусства. Таких, например, как

(4) Число участвует, в названиях различных географических названий.
Причем, иногда многократно в одном и том же названии. Что является, безусловно, уникальным явлением для чисел.
Например, в названии города Tbilisi число встречается трижды.

А в названии реки Mississippi число имеется — аж четыре раза!

(5) Встречались ли вам кулинарные блюда, названные в честь каких-нибудь чисел.
А вот комплексные обеды — существовали в советское время. И до сих пор кое-где существуют!

(6) В новейших достижениях электроники (таких, как iPhone и iPad) число располагают на самом почетном — ПЕРВОМ месте.

Источник

Как легко понять знаки Σ и П с помощью программирования

Для тех, кто подзабыл матешу

Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.

Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.

Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.

Знак Σ — сумма

Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:

Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.

На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:

Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».

Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:

Произведение П

С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:

А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:

Что дальше

Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.

Источник

Новое в блогах

Физическая интерпретация i

В качестве гипотезы интерпретации i в реальности можно предложить следующую идею. Величина мнимой части комплексного числа является вполне реальной величиной, но расположенной за границей рассматриваемого явления, например, за пределами частицы. Умножение комплексного числа на i приводит к переходу самого акта рассмотрения через условную границу частицы, в результате чего мнимая часть становится действительной, а действительная становится мнимой, расположенной за границей рассматриваемой области только теперь уже с другой ее стороны.

Физические уравнения, содержащие мнимую часть, описывают явления внутри частицы, однако внешние явления также оказывают влияние на внутренние явления в частице, но это влияние не полное, поскольку отделено границей.

Сергей Заикин # ответил на комментарий Олег Сазонов 22 октября 2014, 15:00 «Простите, я перестал вас понимать.»

Думаю, что Вы и не собирались.
Что требуется от Вас?
— найти физический смысл «мнимых» величин.
О чем пишете Вы:
— для чего используются мнимые числа
— о мнимой операции
То есть о чем-то о смежном, но ответа на поставленный вопрос нет.
Сосредоточьтесь на физическом смысле переменных, находящихся в мнимой части комплексного числа.
Кстати, это очень важно для выявления критерия различения внутренних и внешних явлений и для различения внешних действий (дальнодействия и близкодейстия) и внутренних действий.

Сергей Заикин # ответил на комментарий Олег Сазонов 22 октября 2014, 16:39 «физического смысла у мнимых величин не существует.»

Олег Сазонов # ответил на комментарий Сергей Заикин 23 октября 2014, 09:03 Жаль, что вы не увидели ответа.

Есть большая разница между реальностью и символами ее описывающими. Если вы даже найдете на хлебе буквы х, л и т.д, то смысла в этом не будет.

Олег, помогите новичку разобраться с мнимой частью, «в реальности».
ссылка на maxpark.com
Подскажите ему каким образом произведение двух мнимых частей может стать действительным числом.
А также прокомментируйте ссылка на forum.if4.ru

Олег Сазонов # ответил на комментарий Олег Сазонов 8 августа 2015, 19:08 Посмотрел.
Но желание «помогать» не возникло. Вы говорите о совершенно разных вещах. Если в ваш разговор влезу еще и я, то это будет всего лишь третья тема, которая будет противоречить (или находиться в другом измерении) по отношению к вашему обсуждению.

Вам же я могу сказать, что, измеряя параметры некоторой электрической схемы на некоторой частоте, мы измеряем полное сопротивление цепи и угол между напряжением и током, что дает нам вектор импеданса. На другой частоте вектор получится иным, но на любой из частот мы можем разложить вектор в плоскости с координатами Re/Im на два ортогональных вектора.
Интересным является поведение конца этого вектора на вышеуказанной плоскости. Если для всех частот отметить точками координаты этого вектора для RC цепи, то они сольются в правильную полуокружность. То же и для RL цепи, только в другом квадранте.
Говорить же о физическом смысле Re и Im не имеет смысла, так как физический смысл не должен зависеть от частоты.

Олег Сазонов # ответил на комментарий valentin markov 22 ноября 2014, 21:28 Терпением.

Я с удовольствием ответил бы на ваши вопросы, но, как я понимаю, они не ко мне. В этом случае лучше обратиться прямо к ним, иначе вашего вопроса они могут не заметить.

Константин Иванов # написал комментарий 4 августа 2015, 17:11 Наше пространство состоит из 3-х проявленных измерений и какого-то кол-ва скрытых измерений, «скрученных» в струны. На микро-уровне эти скрытые измерения могут разворачиваться и участвовать в физических процессах.

К примеру, известная формула Эйнштейна про зависимость массы от скорости. Если скорость объекта выше скорости света, то масса объекта становится комплексной. Т.е. часть массы объекта «уходит» в скрытое измерение. Что и позволяет объекту перемещаться выше скорости света

Константин Иванов # ответил на комментарий Сергей Заикин 7 августа 2015, 14:36 Не вижу никаких злоупотреблений. Суперструны – не абстракция, а физическая теория.

Взаимопереходы мнимых частей и действительных – совершенно неудивительны, если допустить, что это лишь проекции частицы, имеющей мерность не только в обычном 3х-мерном пространстве, но и в свёрнутых, непроявленных измерениях. Не вижу в этом ничего невозможного и невероятного.

Поэтому неудивительно, что проекция энергетического взаимодействия на реальное пространство оказывается зависимой от параметров объекта в скрытом пространстве (и наоборот). Это есть проявление взаимозависимости частей объекта друг от друга.

Константин Иванов # ответил на комментарий Сергей Заикин 8 августа 2015, 13:37 Могу ответить, что то, что Вы усматриваете противоречия не значит, что они там есть на самом деле.

Сергей Заикин # ответил на комментарий Константин Иванов 8 августа 2015, 14:35 Вопросы поставлены о реальности:
Так какими они (мнимые части параметров) являются в реальности?
Чем в реальности отличаются Еr и Em?

Разумеется, между проявленными и непроявленными измерениями есть разница. На макро-уровне мы можем видеть, чувствовать и измерять только Re-проекцию комплексного пространства и комплексных частиц. Скрытые измерения проявляются только на уровне микро-мира, соответствующего размеру суперструн

Константин Иванов # ответил на комментарий Сергей Заикин 8 августа 2015, 17:56 Не уклоняюсь, а уточняю.
А то мало ли ещё какие общепринятые концепции, Вы исключите из реальности и причислите к «инструментам мышления».

Математика и физика не отказывает пространству в реальности. И я не вижу причин делать это.

Источник

Числовые и буквенные выражения. Формулы

Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:

Буквы и цифры в математике служат для обозначения чисел.

Цифрами обозначается конкретное, какое-то определённое число.

Буквами – любое или неизвестное число, в зависимости от задачи.

МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:

При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.

Примеры математических выражений:

ВНИМАНИЕ!

НЕ ЯВЛЯЕТСЯ математическим выражением:

Например, это НЕ математические выражения:

Случаи опускания знака умножения в выражениях

В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.

В остальных случаях знак умножения опускают, например:

Как читать математические выражения

Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:

Более сложные выражения, называют по последнему выполняемому действию:

Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:

Алгоритм чтения математических выражений

Чтобы прочитать математическое выражение, нужно:

При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.

Формулы

Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.

Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:

а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);

б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_

= v_<1>-15\).

Иначе это называется выразить одну величину через другую.

Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.

Запись такого равенства называется формулой.

ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.3 / 5. Количество оценок: 8

Источник

Три самые известные математические константы: как они появились и зачем нужны

В основе нашей Вселенной стоят числа, также известные как фундаментальные константы. Они показывают, как движутся галактики, как расширяется Вселенная, как вообще работает пространство и время. Рассказываем, кто их открыл и за что отвечает каждое число.

Читайте «Хайтек» в

Что такое математическая константа?

В противоположность переменным величинам существуют математические постоянные. Математическая постоянная, или константа — это величина, значение которой неизменно. Главной отличительной чертой математических констант является их независимость от физических измерений. Все математические константы имеют буквенный символ.

Число Пи

Число Пи (π) — это математическая константа, равная отношению длины окружности к ее диаметру. Десятичное представление числа никогда не заканчивается и является эталоном для высокопроизводительных вычислений.

Чему равно: 3,1415926535…

На сегодняшний день число Пи рассчитали с точностью до 62,8 трлн знаков после запятой — с помощью 32-ядерных процессоров AMD.

Если измерить веревкой длину окружности, получится, что она равна приблизительно трем ее диаметрам. Человечество выяснило это еще в древности. Кстати, это соотношение подходит для любой окружности — неважно, речь о часах или колесе обозрения. Иными словами, все окружности в мире связаны этой математической константой. Еще до нашей эры люди знали, что это число чуть больше трех. Вопрос в том, насколько. Столетия эта загадка не давала покоя мыслителям, поскольку имела большое значение и была почти высчитана. Но это «почти» растянулось на несколько тысяч лет.

Точное авторство числа Пи неизвестно. Вообще, открытие приписывается древним индийцам, грекам, китайцам и прочим хорошим людям. Впервые обозначил его греческой буквой π в начале XVIII века английский математик Уильям Джонс.

Числу π столько же лет, сколько всей математике: около 4 тыс. Старейшие шумерские таблички приводят для него цифру 25/8, или 3,125. Ошибка — меньше процента. Вавилоняне абстрактной математикой особо не увлекались, так что π вывели опытным путем, просто измеряя длину окружностей. Кстати, это первый эксперимент по численному моделированию мира.

Число Бога

Число Фи (φ) — число Бога, Золотое Сечение, Золотая Пропорция — у него много названий. Сам по себе это отношение одной части чего-либо к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%.

Чему равно: 1,6180339887…

Классическое определение Золотой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.

Принято считать, что впервые закономерности соотношения размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 году немецкий исследователь Цейзинг в своем научном труде «Эстетические исследования». За основу своей теории он взял учение о Золотом Сечении.

Еще в VI веке до н. э. древнегреческий философ и математик Пифагор ввел в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

История Золотого Сечения связана еще с одним известным итальянским математиком Фибоначчи. До наших времен дошел ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению Золотого Сечения (21:34=0,617, а 34:55=0,618). Впоследствии все исследователи Золотого Сечения в растительном и животном мире, искусстве и анатомии приходили к этому ряду как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибоначчи вывел, подсчитывая количество рожденных кроликов от пары кроликов за год.

Число Непера

Число е — своего рода двойник π. Если π отвечает за пространство, то е — за время, и тоже проявляет себя почти всюду. Скажем, радиоактивность полония-210 уменьшается в е раз за средний срок жизни одного атома, а раковина моллюска Nautilus — это график степеней е, обернутый вокруг оси.

Чему равно: 2,718281828…

е — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда его называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Иными словами, число е является базовым соотношением роста для всех непрерывно растущих процессов. Оно участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов и других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е — это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Число открыл Джон Непер, шотландский математик, в 1618 году. Самого числа он не упоминал, зато выстроил на его основе свои таблицы логарифмов. Одновременно кандидатами в авторы константы считаются Якоб Бернулли, Лейбниц, Гюйгенс и Эйлер. Достоверно известно только то, что символ е взялся из фамилии последнего.

Как и π, е — трансцендентное число. Говоря проще, его нельзя выразить через дроби и корни. Есть гипотеза, что у таких чисел в бесконечном «хвосте» после запятой встречаются все комбинации цифр, какие только возможны.

Источник