Булевая функция что это
Определение булевой функции
Содержание
Основные сведения [ править ]
| Таблица истинности | |||||
|---|---|---|---|---|---|
| [math]x_1[/math] | [math]x_2[/math] | [math]\ldots[/math] | [math]x_n[/math] | [math]f(x_1,x_2,\ldots,x_n)[/math] | |
| [math]0[/math] | [math]0[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(0,0,\ldots,0)[/math] | |
| [math]1[/math] | [math]0[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(1,0,\ldots,0)[/math] | |
| [math]0[/math] | [math]1[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(0,1,\ldots,0)[/math] | |
| [math]1[/math] | [math]1[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(1,1,\ldots,0)[/math] | |
| [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | |
| [math]0[/math] | [math]1[/math] | [math]\ldots[/math] | [math]1[/math] | [math]f(0,1,\ldots,1)[/math] | |
| [math]1[/math] | [math]1[/math] | [math]\ldots[/math] | [math]1[/math] | [math]f(1,1,\ldots,1)[/math] | |
Практически все булевы функции малых арностей ( [math]0, 1, 2[/math] и [math]3[/math] ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).
Нульарные функции [ править ]
Унарные функции [ править ]
Таблица значений булевых функций от одной переменной:
| Функции от одной переменной | ||||
|---|---|---|---|---|
| [math]0[/math] | [math]x[/math] | [math]\neg x[/math] | [math]1[/math] | |
| 0 | [math]0[/math] | [math]0[/math] | [math]1[/math] | [math]1[/math] |
| 1 | [math]0[/math] | [math]1[/math] | [math]0[/math] | [math]1[/math] |
| Сохраняет 0 | ✓ | ✓ | ||
| Сохраняет 1 | ✓ | ✓ | ||
| Самодвойственная | ✓ | ✓ | ||
| Монотонная | ✓ | ✓ | ✓ | |
| Линейная | ✓ | ✓ | ✓ | ✓ |
Названия булевых функций от одной переменной:
| Обозначение | Название |
|---|---|
| [math]0[/math] | тождественный ноль, тождественная ложь, тождественное «НЕТ» |
| [math]x[/math] | тождественная функция, логическое «ДА», «YES»(англ.) |
| [math]\bar x,\ \neg x,\ x'[/math] | отрицание, логическое «НЕТ», «НЕ», «НИ», «NOT»(англ.), «NO»(англ.) |
| [math]1[/math] | тождественная единица, тождественная истина, тождественное «ДА», тавтология |
Бинарные функции [ править ]
Таблица значений булевых функций от двух переменных:
| Функции от двух переменных: | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | [math]0[/math] | [math]x \land y[/math] | [math]x \nrightarrow y[/math] | [math]x[/math] | [math]x \nleftarrow y[/math] | [math]y[/math] | [math]x \oplus y[/math] | [math]x \lor y[/math] | [math]x \downarrow y[/math] | [math]x = y[/math] | [math]\neg y[/math] | [math]x \leftarrow y[/math] | [math]\neg x[/math] | [math]x \rightarrow y[/math] | [math]x \triangledown y[/math] | [math]1[/math] |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Сохраняет 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Сохраняет 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Самодвойственная | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| Монотонная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Линейная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
Названия булевых функций от двух переменных:
| Обозначение | Другие обозначения | Название |
|---|---|---|
| [math]0[/math] | тождественный ноль, тождественная ложь, тождественное «НЕТ» | |
| [math]x \land y[/math] | [math]x \cdot y,\ xy,\ x \And y,\ x\ AND\ y,\ AND(x, y),\ min(x, y), x [/math] И [math]y,[/math] И [math](x, y)[/math] | 2И, конъюнкция |
| [math]x \nrightarrow y[/math] | [math]x \gt y,\ \neg(x \rightarrow y),\ x\ GT\ y,\ GT(x,\ y)[/math] | больше, инверсия прямой импликации |
| [math]x[/math] | [math]YES1(x,y),[/math] ДА1 [math](x, y)[/math] | первый операнд |
| [math]x \nleftarrow y[/math] | [math]x \lt y,\ \neg(x \leftarrow y),\ x\ LT\ y,\ LT(x, y)[/math] | меньше, инверсия обратной импликации |
| [math]y[/math] | [math]YES2(x, y),[/math] ДА2 [math](x, y)[/math] | второй операнд |
| [math]x \oplus y[/math] | [math]x + _2 y,\ x \not = y,\ x \gt \lt y,\ x \lt \gt y,\ x\ XOR\ y,\ XOR(x,y)[/math] | сложение по модулю 2, не равно, ксор, исключающее «или» |
| [math]x \lor y[/math] | [math]x + y,\ x\ OR\ y,\ OR(x,y),\ max(x,y),[/math] [math]x [/math] ИЛИ [math]y,[/math] ИЛИ [math](x, y)[/math] | 2ИЛИ, дизъюнкция |
| [math]x \downarrow y[/math] | [math]x\ NOR\ y,\ NOR(x,y)[/math] [math]x [/math] ИЛИ-НЕ [math]y,[/math] ИЛИ-НЕ [math](x, y)[/math] | НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса |
| [math]x = y[/math] | [math]x \equiv y, x EQV y, EQV(x,y), x \sim y, x \leftrightarrow y[/math] | равенство, эквивалентность |
| [math]\neg y[/math] | [math]NOT2(x, y),\ y’,\ \bar | отрицание (негация, инверсия) второго операнда |
| [math]x \leftarrow y[/math] | [math]x \geq y,\ x \subset y,\ x\ GE\ y,\ GE(x, y)[/math] | больше или равно, обратная импликация (от второго аргумента к первому) |
| [math]\neg x[/math] | [math]NOT1(x,y),\ x’,\ \bar | отрицание (негация, инверсия) первого операнда |
| [math]x \rightarrow y[/math] | [math]x \leq y,\ x \supset y,\ x\ LE\ y,\ LE(x,y)[/math] | меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму) |
| [math]x \triangledown y[/math] | [math]x \mid y,\ x\ NAND\ y,\ NAND(x,y),[/math] [math]x [/math] И-НЕ [math]y,[/math] И-НЕ [math](x, y)[/math] | НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера |
| [math]1[/math] | тождественная единица, тождественная истина, тождественное «ДА», тавтология |
Тернарные функции [ править ]
| Таблица истинности некоторых тернарных функций | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]x[/math] | [math]y[/math] | [math]z[/math] | [math]x \downarrow y \downarrow z[/math] | [math]\neg (\geq 2(x,y,z))[/math] | [math]x \not = y \not = z[/math] | [math]x \mid y \mid z[/math] | [math]min(x,y,z)[/math] | [math]x=y=z[/math] | [math]x \oplus y \oplus z[/math] | [math]\geq 2(x,y,z)[/math] | [math]f_1[/math] | [math]f_2[/math] | [math]max(x,y,z)[/math] |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Названия булевых функций трех переменных:
| Обозначения | Другие обозначения | Названия |
|---|---|---|
| [math]x \downarrow y \downarrow z[/math] | [math]\downarrow (x,y,z) = Webb_2 (x,y,z)[/math] | 3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса |
| [math]\neg (\geq 2(x,y,z))[/math] | Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией | |
| [math]x \not = y \not = z[/math] | [math][\not =(x,y,z)] = NE(x,y,z)[/math] | Неравенство |
| [math]x \mid y \mid z[/math] | [math]\mid(x,y,z)[/math] | 3-И-НЕ, штрих Шеффера |
| [math]x \land y \land z[/math] | [math]\land (x,y,z) = (x\ AND\ y\ AND\ z) = AND(x,y,z) = min(x,y,z) = \lt br/\gt (x[/math] И [math] y[/math] И [math] z) = [/math] И [math](x,y,z)[/math] | 3-И, минимум |
| [math]x=y=z[/math] | [math][=(x,y,z)] = EQV(x,y,z)[/math] | Равенство |
| [math]x \oplus y \oplus z[/math] | [math]x +_2 y +_2 z = \oplus (x,y,z) = +_2 (x,y,z)[/math] | Тернарное сложение по модулю 2 |
| [math]\geq 2(x,y,z)[/math] | [math](x [/math] И [math]y) [/math] ИЛИ [math](y[/math] И [math] z)[/math] ИЛИ [math](z [/math] И [math] x)[/math] | переключатель по большинству, 3-ППБ, мажоритарный клапан |
| [math]f_1[/math] | Разряд займа при тернарном вычитании | |
| [math]f_2[/math] | Разряд переноса при тернарном сложении | |
| [math]x+y+z[/math] | [math]+(x,y,z) = max(x,y,z) = (x\ OR\ y\ OR\ z) = OR(x,y,z) = (x [/math] ИЛИ [math] y [/math] ИЛИ [math] z) = [/math] ИЛИ [math](x,y,z)[/math] | 3-ИЛИ, максимум |
Представление функции формулой [ править ]
Тождественность и двойственность [ править ]
| Определение: |
| Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. |
Тождественность функций f и g можно записать, например, так:
[math]f(x_1, x_2, \dots, x_n)=g(x_1, x_2, \dots, x_n)[/math]
Просмотрев таблицы истинности булевых функций, легко получить такие тождества:
| [math]\overline<0>=1[/math] | [math]\overline<1>=0[/math] | [math]\overline<\overline | [math]x \land y=y \land x\![/math] | [math]x\lor y=y \lor x[/math] |
| [math]0 \land x=0\![/math] | [math]1 \land x=x\![/math] | [math]0 \lor x=x[/math] | [math]1\lor x=1[/math] | [math]x \land x=x \lor x=x[/math] |
А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:
| [math]x \land \overline | [math]x \lor \overline |
| [math]\overline | [math]\overline | (законы де Моргана) |
[math]x \land (y\lor z)=(x \land y)\lor (x \land z)[/math]
[math]x \lor (y \land z)=(x\lor y) \land (x\lor z)[/math] (дистрибутивность конъюнкции и дизъюнкции)
Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.
Суперпозиции [ править ]
| Определение: |
| Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных. |
Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.
Полнота системы, критерий Поста [ править ]
| Определение: |
| Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества. |
| Определение: |
| Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций. |
Американский математик Эмиль Пост [1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:
Представление булевых функций [ править ]
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ) [ править ]
| Определение: |
| Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов. |
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.
Конъюнктивная нормальная форма (КНФ) [ править ]
| Определение: |
| Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. |
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.
[math]f(x,y,z) = (x \lor y) \land (y \lor \neg
[math]f(x,y,z,t) = (x \lor t) \land (y \lor \neg
[math]f(x,y,z,t,m) = (x \lor m \lor \neg
Полином Жегалкина [ править ]
Полином Жегалкина имеет следующий вид:
[math]P = a_ <000\ldots000>\oplus a_ <100\ldots0>x_1 \oplus a_ <010\ldots0>x_2 \oplus \ldots \oplus a_ <00\ldots01>x_n \oplus a_ <110\ldots0>x_1 x_2 \oplus \ldots \oplus a_ <00\ldots011>x_
[math]f(x_1,x_2) = 1 \oplus x_1 \oplus x_1 x_2 [/math]
[math]f(x_1,x_2,x_3) = x_1 \oplus x_1 x_2 \oplus x_2 x_3 [/math]
[math]f(x_1,x_2,x_3,x_4) = 1 \oplus x_1 \oplus x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 x_2 x_4 [/math]
Тождественные функции. Выражение функций друг через друга [ править ]
| Определение: |
| Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения. |
Приведение тождественной функции есть выражение булевой функции через другие.
Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.
[math] x \oplus y = \left ( x \land \lnot y \right ) \lor \left ( \lnot x \land y \right ) = \left ( x \lor \lnot y \right ) \land \left ( \lnot x \lor y \right )[/math]
[math] x \downarrow y = \lnot \left ( x \lor y \right) = \lnot x \land \lnot y[/math]
[math]\langle x, y, z \rangle = \left ( x \land y \right ) \lor \left ( y \land z \right ) \lor \left ( x \land z \right ) = \left ( x \lor y \right ) \land \left ( y \lor z \right ) \land \left ( x \lor z \right )[/math]
Подстановка одной функции в другую [ править ]
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.
Отождествление переменных [ править ]
| Пример: |
| [math] f(a,b) = a \vee b [/math] — исходная функция [math] h(a) = a \vee a [/math] — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию [math]P_<1>[/math] — проектор единственного аргумента. |
Схемы из функциональных элементов [ править ]
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
 |  |  |  |  |
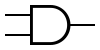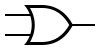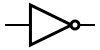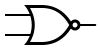Стандартный базис [ править ]
[math] x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) [/math]
[math] x \rightarrow y = \lnot x \lor y [/math]
[math] 0 = x \land \lnot x [/math]
Функции [math] \mid \ и \downarrow[/math] являются отрицаниями функций [math] \land \ и \ \lor[/math] соответственно.
[math] x \mid y = \lnot \left ( x \land y \right )[/math]
[math] x \downarrow y = \lnot \left ( x \lor y \right )[/math]
Тождественность функций можно доказать с помощью таблицы истинности.
[math]x \leftarrow y = \lnot x \rightarrow \lnot y = x \lor \lnot y [/math]
Полнота стандартного базиса [ править ]
[math] x \land y = \lnot \left (\lnot x \lor \lnot y \right ) [/math]
[math] x \lor y = \lnot \left (\lnot x \land \lnot y \right ) [/math]
Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:
Теоремы о числе функций в базисе [ править ]
Значит, так как [math]X[/math] — безызбыточный базис, а система [math]\
Приведём примеры базисов для каждого [math]k[/math] :
[math]k = 1 \Rightarrow X = \< \downarrow \>[/math] ;
[math]k = 2 \Rightarrow X = \< \lnot, \land \>[/math] ;
Докажем, что последняя система является базисом:
Булевая функция что это
2.1 рТЕДУФБЧМЕОЙЕ МПЗЙЮЕУЛЙИ ЖХОЛГЙК
 |
| тЙУХОПЛ 1 |
ѓX = 1\и ; и 
Y = и × Y = min(X,Y);
уХННБ РП НПДХМА 2 ЛБЛ ВЙОБТОБС ПРЕТБГЙС ПВМБДБЕФ УЧПКУФЧБНЙ ЛПННХФБФЙЧОПУФЙ Й БУУПГЙБФЙЧОПУФЙ
(Б 
b) У = Б (b У), Й РПЬФПНХ ЕЕ НПЦОП ЪБРЙУЩЧБФШ ВЕЪ УЛПВПЛ Б b У Й РЕТЕУФБЧМСФШ УМБЗБЕНЩЕ.
чБЦОЩК РТЙНЕТ РТЙНЕОЕОЙС ВХМЕЧЩИ ЖХОЛГЙК ДБАФ БТЙЖНЕФЙЮЕУЛЙЕ ДЕКУФЧЙС ОБД ДЧПЙЮОЩНЙ ЮЙУМБНЙ: РПУЛПМШЛХ ЧПЪНПЦОЩЕ ЪОБЛЙ Ч ДЧПЙЮОПК УЙУФЕНЕ УХФШ 0 Й 1, ФП ЪБЧЙУЙНПУФЙ ЪОБЛПЧ ТЕЪХМШФБФБ ПФ ЪОБЛПЧ УМБЗБЕНЩИ/УПНОПЦЙФЕМЕК ЧЩТБЦБАФУС ВХМЕЧЩНЙ ЖХОЛГЙСНЙ. рТЙ УМПЦЕОЙЙ ДЧХИ ПДОПЪОБЮОЩИ ДЧПЙЮОЩИ ЮЙУЕМ б Й ч ЪОБЛ УХННЩ Ч НМБДЫЕН ТБЪТСДЕ ТБЧЕО (AB), Б ЪОБЛ РЕТЕОПУБσ ЧПЪОЙЛБЕФ ФПМШЛП ЕУМЙ ПВБ УМБЗБЕНЩИ ТБЧОЩ 1, Ф.Е. σ= бч. хНОПЦЕОЙЕ ПДОПЪОБЮОЩИ ДЧПЙЮОЩИ ЮЙУЕМ ФПЦДЕУФЧЕООП ЛПОЯАОЛГЙЙ, ЮФП ЖБЛФЙЮЕУЛЙ ПФНЕЮЕОП ЧЩЫЕ.
| X | 0 | X | ѓX | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| X | Y | XY | X Y | X Y | X Y | XY | X | Y |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| X | Y | Z | m3 | g1 | g2 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
нОПЦЕУФЧП ЧУЕИ МПЗЙЮЕУЛЙИ ЖХОЛГЙК, ПФ МАВПЗП ЛПОЕЮОПЗП ЮЙУМБ РЕТЕНЕООЩИ ПВПЪОБЮБЕФУС т2.
чЩУЛБЪЩЧБОЙС Й РТЕДЙЛБФЩ
пУОПЧОЩН РПОСФЙЕН НБФЕНБФЙЮЕУЛПК МПЗЙЛЙ СЧМСЕФУС РПОСФЙЕ ЧЩУЛБЪЩЧБОЙС.
чЩУЛБЪЩЧБОЙЕН ОБЪЩЧБЕФУС РПЧЕУФЧПЧБФЕМШОПЕ РТЕДМПЦЕОЙЕ, ЛПФПТПЕ НПЦЕФ ВЩФШ МЙВП ЙУФЙООЩН, МЙВП МПЦОЩН.
рТЙНЕТ
рТЕДМПЦЕОЙС, Ч ЛПФПТЩЕ ЧИПДСФ РЕТЕНЕООЩЕ Й ЛПФПТЩЕ РТЙ ЪБНЕОЕ ЬФЙИ РЕТЕНЕООЩИ ЙИ ЪОБЮЕОЙСНЙ УФБОПЧСФУС ЧЩУЛБЪЩЧБОЙСНЙ, ОБЪЩЧБАФ ЧЩУЛБЪЩЧБФЕМШОЩНЙ ЖПТНБНЙ ЙМЙ РТЕДЙЛБФБНЙ. рТЙ ЬФПН ДПМЦОП ВЩФШ ЪБДБОП НОПЦЕУФЧП X, ЛПФПТПЕ НПЦЕФ РТЙОЙНБФШ РЕТЕНЕООБС И, ЕУМЙ РТЕДЙЛБФ У ПДОПК РЕТЕНЕООПК (ПДОПНЕУФОЩК РТЕДЙЛБФ).
нОПЦЕУФЧП ф ЪОБЮЕОЙК РЕТЕНЕООПК РТЙ РПДУФБОПЧЛЕ ЛПФПТЩИ Ч РТЕДЙЛБФ РПМХЮБЕФУС ЙУФЙООПЕ ЧЩУЛБЪЩЧБОЙЕ, ОБЪЩЧБАФ НОПЦЕУФЧПН ЙУФЙООПУФЙ РТЕДЙЛБФБ.
еУМЙ РТЕДЙЛБФ ДЧХНЕУФОЩК ( У ДЧХНС РЕТЕНЕООЩНЙ), ФТЕИНЕУФОЩК Й Ф.Д., ФП ДМС ЛБЦДПЗП РЕТЕНЕООПЗП ДПМЦОП ВЩФШ ХЛБЪБОП НОПЦЕУФЧП ЕЗП ЪОБЮЕОЙК.
лЧБОФПТЩ
ч ЖПТНХМЙТПЧЛБИ ТБЪМЙЮОЩИ НБФЕНБФЙЮЕУЛЙИ РТЕДМПЦЕОЙК ЮБУФП ЧУФТЕЮБАФУС УМПЧБ «ОЕЛПФПТЩЕ», «ЧУЕ», «ЛБЦДЩК» Й ЙИ УЙОПОЙНЩ.
тБУУНПФТЕООЩЕ РТЙНЕТЩ РПМХЮЕОЙС ЧЩУЛБЪЩЧБОЙК У РПНПЭША ЛЧБОФПТПЧ ПФОПУЙМЙУШ Л ПДОПНЕУФОЩН ЧЩУЛБЪЩЧБФЕМШОЩН ЖПТНБН (ПДОПНЕУФОЩН РТЕДЙЛБФБН). чУЕ УЛБЪБООПЕ ПУФБЕФУС УРТБЧЕДМЙЧЩН Й ДМС НОПЗПНЕУФОЩИ ЧЩУЛБЪЩЧБФЕМШОЩИ ЖПТН, ОП РТЙ ЬФЙН ОБДП ЙНЕФШ Ч ЧЙДХ, ЮФП Ч РПДПВОЩИ УМХЮБСИ ДМС РПМХЮЕОЙС ЧЩУЛБЪЩЧБОЙК ОБДП УЧСЪБФШ ЛЧБОФПТПН ЛБЦДХА РЕТЕНЕООХА.
рТЙНЕТ
хЦЕ ЗПЧПТЙМПУШ, ЮФП Ч НБФЕНБФЙЛЕ ПДОПК ЙЪ ЧБЦОЕКЫЙИ ЪБДБЮ СЧМСЕФУС ХУФБОПЧМЕОЙЕ ЪОБЮЕОЙС ЙУФЙООПУФЙ ЧЩУЛБЪЩЧБОЙК. чЩСУОЙН, ЛБЛ ХУФБОБЧМЙЧБАФ ЪОБЮЕОЙС ЙУФЙООПУФЙ ЧЩУЛБЪЩЧБОЙК У ЛЧБОФПТБНЙ.
ч ЧЩУЛБЪЩЧБОЙЙ (
И
и) F(x) ХФЧЕТЦДБЕФУС, ЮФП ДМС МАВПЗП И ЙЪ НОПЦЕУФЧБ и ЙУФЙООП F(x), РПЬФПНХ ЮФПВЩ ХВЕДЙФШУС Ч ЙУФЙООПУФЙ ЬФПЗП ЧЩУЛБЪЩЧБОЙС, ОБДП РПЛБЪБФШ, ЮФП НОПЦЕУФЧП ф ЙУФЙООПУФЙ ЧЩУЛБЪЩЧБФЕМШОПК ЖПТНЩ F(x) УПЧРБДБЕФ У НОПЦЕУФЧПН X. юФПВЩ ХВЕДЙФШУС Ч МПЦОПУФЙ ЧЩУЛБЪЩЧБОЙС (Ии) F(x) ДПУФБФПЮОП РПЛБЪБФШ, ЮФП ф
и, ФП ЕУФШ ДПЛБЪБФШ, ЮФП УХЭЕУФЧХЕФ ФБЛПЕ ЪОБЮЕОЙЕ И, РТЙ ЛПФПТПН ЧЩУЛБЪЩЧБФЕМШОБС ЖПТНБ ПВТБЭБЕФУС Ч ЦЕМБЕНПЕ ЧЩУЛБЪЩЧБОЙЕ.
чППВЭЕ, ЙУФЙООПУФШ ЧЩУЛБЪЩЧБОЙС У ЛЧБОФПТПН ПВЭОПУФЙ ХУФБОБЧМЙЧБЕФУС РХФЕН ДПЛБЪБФЕМШУФЧБ. рПЛБЪБФШ МПЦОПУФШ ФБЛЙИ ЧЩУЛБЪЩЧБОЙК НПЦОП, РТЙЧЕДС ЛПОФТРТЙНЕТ.
чЩСУОЙН, ЛБЛ ХУФБОБЧМЙЧБЕФУС ЪОБЮЕОЙЕ ЙУФЙООПУФЙ ЧЩУЛБЪЩЧБОЙК У ЛЧБОФПТПН УХЭЕУФЧПЧБОЙС.
ч ЧЩУЛБЪЩЧБОЙЙ (
И) F(x) ХФЧЕТЦДБЕФУС, ЮФП Ч НОПЦЕУФЧЕ и ЕУФШ ФБЛПК ЬМЕНЕОФ И, ЛПФПТЩК ПВМБДБЕФ УЧПКУФЧПН F. рПЬФПНХ ПОП ВХДЕФ ЙУФЙООП, ЕУМЙ НОПЦЕУФЧП ЙУФЙООПУФЙ ЧЩУЛБЪЩЧБФЕМШОПК ЖПТНЩ F(x) ОЕ РХУФП. дМС ФПЗП ЮФПВЩ РПЛБЪБФШ ЬФП, ДПУФБФПЮОП ОБКФЙ ФБЛПЕ ЪОБЮЕОЙЕ РЕТЕНЕООПК И, РТЙ ЛПФПТПН ЧЩУЛБЪЩЧБФЕМШОБС ЖПТНБ F(x) ПВТБЭБЕФУС Ч ЙУФЙООПЕ ЧЩУЛБЪЩЧБОЙЕ, ФП ЕУФШ РТЙЧЕУФЙ РТЙНЕТ. фБЛ, ЧЩУЛБЪЩЧБОЙЕ «ОЕЛПФПТЩЕ ОБФХТБМШОЩЕ ЮЙУМБ ДЧХЪОБЮОЩЕ» НПЦОП УЮЙФБФШ ЙУФЙООЩН, ФБЛ ЛБЛ 36 ДЕКУФЧЙФЕМШОП ДЧХЪОБЮОПЕ ЮЙУМП.
чЩУЛБЪЩЧБОЙЕ (И) F(x) МПЦОП Ч ФПН УМХЮБЕ, ЛПЗДБ ф=ø ХВЕДЙФШУС Ч ЬФПН НПЦОП МЙЫШ РХФЕН ДПЛБЪБФЕМШУФЧБ.
фБЛЙН ПВТБЪПН, ЙУФЙООПУФШ ЧЩУЛБЪЩЧБОЙС У ЛЧБОФПТПН УХЭЕУФЧПЧБОЙС ХУФБОБЧМЙЧБЕФУС РТЙ РПНПЭЙ ЛПОЛТЕФОПЗП РТЙЕНБ. юФПВЩ ХВЕДЙФШУС Ч МПЦОПУФЙ ФБЛПЗП ЧЩУЛБЪЩЧБОЙС, ОЕПВИПДЙНП РТПЧЕУФЙ ДПЛБЪБФЕМШУФЧП.