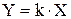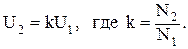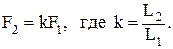что означает множественность модели
Множественность и единство моделей
Принципы построения моделей
С одной стороны, реальная система может иметь несколько совершенно различных моделей, с другой стороны – одна и та же математическая конструкция может представлять различные системы.
Множественность объясняется, во первых, необходимостью исследования различных свойств системы. Во вторых – необходимостью решения различных задач исследования.
В качестве примера из квантовой физики. Нильс Бор в 1913 году построил графическую модель ядра водорода, которая предполагает наличие стационарных орбит движения электрона, и достаточно хорошо описывает свойства его поведения как частицы. Модель Шредингера (уравнение Шредингера) определяет вид волновой функции, то есть фактически описывает поведение электрона как волны. Это пример множественности моделей одного объекта для описания различных свойств (корпускулярные и волновые свойства элементарных частиц).
Единство моделей объясняется в первую очередь тем, что любая математическая конструкция может представлять собой модель различных систем.
Например, рассмотрим самую простую линейную зависимость
Это простейший вид функциональной зависимости – прямая пропорциональная зависимость переменной Y от переменной Х, к – коэффициент пропорциональности. Графически пропорциональная зависимость изображается прямой линией, проходящей через начало координат, угловой коэффициент которой равен коэффициенту пропорциональности.
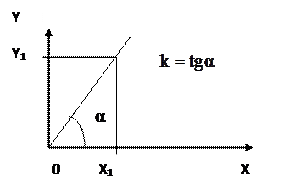 |
Рис. 2. Пропорциональная зависимость
Эта математическая формула может рассматриваться в качестве модели, например, усилителя напряжения или трансформатора.
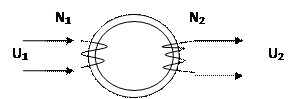 |
Рис.3. Схема трансформатора
Трансформатор – устройство для повышения или понижения напряжения переменного тока (действие основано на явлении магнитной индукции).
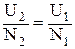
Таким образом, формула пропорциональности есть модель процесса трансформации напряжения.
Эта та же формула может служить моделью и другой системы. Например, моделью рычага
 |
Рычаг описывается следующим соотношением
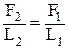
Если различные объекты имеют одинаковую модель, то возможно моделировать один объект другим.
2. Свойство конечности моделей.
Модель отображает оригинал лишь в конечном числе его отношений. Любая модель имеет ограничения. Эти ограничения устанавливает разработчик в зависимости от целей исследования.
Формула не может описывать всех свойств системы. Формула должна быть адекватна только исследуемым свойствам объекта.
Например, если мы исследуем процесс трансформации напряжения в установленных нормативах, то представленная выше модель пропорциональной зависимости адекватна. А если нам необходимо исследовать процесс магнитной индукции, то мы не получим линейной зависимости на всем диапазоне изменения аргумента, поскольку существует эффект насыщения магнитного сердечника. А еще здесь присутствует гистерезис. Для исследования этих свойств нужна уже другая модель.
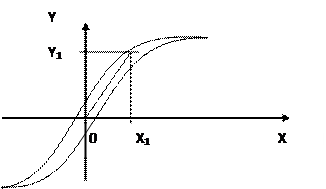 |
Рис. 5. Эффекта гистерезиса.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Mangeshine
Одним из основополагающих принципов моделирования сложных систем является принцип множественности моделей, заключающийся, с одной стороны, в возможности отображения многих различных систем и процессов с помощью одной и той же модели и, с другой стороны, в возможности представления одной и той же системы множеством различных моделей в зависимости от целей исследования. Использование этого принципа позволяет отказаться от подхода, когда для каждой исследуемой системы разрабатывается своя модель, и предложить новый подход, при котором разрабатываются абстрактные математические модели разного уровня (в основном базовые и локальные), используемые для исследования систем различных классов. При этом задача моделирования сводится к грамотной параметризации моделей и интерпретации полученных результатов.
Цель представляет собой сложное сочетание различных противоречивых интересов. Цель является системообразующим, интегрирующим фактором, объединяющим отдельные предметы и процессы в целостность, в систему. Это объединение происходит, исходя из того, что разрозненные предметы далеко не всегда могут служить достаточными средствами для достижения целей человека. А в объединенном виде они приобретают новое, системное, интегральное качество, которое является достаточным для реализации целей.
Система есть средство достижения цели.
Первое определение системы дополняется вторым, характеризующим ее внутреннее строение.
Общее определение системы формулируется следующим образом: «Системой называется совокупность взаимодействующих между собой элементов, выделенных из окружающей среды с определенной целью».
Проблемой называется ситуация, характеризующаяся различием между необходимым (желаемым) выходом и существующим выходом. Выход является необходимым, если его отсутствие создает угрозу существованию или развитию системы. Существующий выход обеспечивается существующей системой. Желаемый выход обеспечивается желаемой системой. Проблема есть разница между существующей и желаемой системой. Проблема может заключаться в предотвращении уменьшения выхода или же в увеличении выхода. Условие проблемы представляет существующую систему («известное»). Требование представляет желаемую систему.
Основы системного анализа

Свойства любой модели таковы:
Жизненный цикл моделируемой системы:
· Сбор информации об объекте, выдвижение гипотез, предмодельный анализ;
· Проектирование структуры и состава моделей (подмоделей);
· Построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей;
· Исследование адекватности, устойчивости, чувствительности модели;
· Оценка средств моделирования (затраченных ресурсов);
· Уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью моделирования.
Множественность моделей систем. Определение понятия «проблема», «цель», «система»
Одним из основополагающих принципов моделирования сложных систем является принцип множественности моделей, заключающийся, с одной стороны, в возможности отображения многих различных систем и процессов с помощью одной и той же модели и, с другой стороны, в возможности представления одной и той же системы множеством различных моделей в зависимости от целей исследования. Использование этого принципа позволяет отказаться от подхода, когда для каждой исследуемой системы разрабатывается своя модель, и предложить новый подход, при котором разрабатываются абстрактные математические модели разного уровня (в основном базовые и локальные), используемые для исследования систем различных классов. При этом задача моделирования сводится к грамотной параметризации моделей и интерпретации полученных результатов.
Цель представляет собой сложное сочетание различных противоречивых интересов. Цель является системообразующим, интегрирующим фактором, объединяющим отдельные предметы и процессы в целостность, в систему. Это объединение происходит, исходя из того, что разрозненные предметы далеко не всегда могут служить достаточными средствами для достижения целей человека. А в объединенном виде они приобретают новое, системное, интегральное качество, которое является достаточным для реализации целей.
Система есть средство достижения цели.
Первое определение системы дополняется вторым, характеризующим ее внутреннее строение.
Общее определение системы формулируется следующим образом: «Системой называется совокупность взаимодействующих между собой элементов, выделенных из окружающей среды с определенной целью».
Проблемой называется ситуация, характеризующаяся различием между необходимым (желаемым) выходом и существующим выходом. Выход является необходимым, если его отсутствие создает угрозу существованию или развитию системы. Существующий выход обеспечивается существующей системой. Желаемый выход обеспечивается желаемой системой. Проблема есть разница между существующей и желаемой системой. Проблема может заключаться в предотвращении уменьшения выхода или же в увеличении выхода. Условие проблемы представляет существующую систему («известное»). Требование представляет желаемую систему.
«Черный ящик». Модель, свойства, трудности построения модели. Условия полезности модели «черного ящика»
Построение модели «черного ящика» может быть сложной задачей из-за множественности входов и выходов системы (это обусловлено тем, что всякая реальная система взаимодействует с окружающей средой неограниченным числом способов). При построении модели из них надо отобрать конечное число. Критерием отбора является целевое назначение модели, существенность той ли иной связи по отношению к этой цели. Здесь, конечно, возможны ошибки, как раз не включенные в модель связи (которые все равно действуют) могут оказаться важными. Особое значение это имеет при определении цели, т.е. выходов системы. Реальная система вступает во взаимодействие со всеми объектами окружающей Среды, поэтому важно учесть все наиболее существенное. В результате главная цель сопровождается заданием дополнительных целей.
Модель черного ящика иногда оказывается единственно применимой при изучении систем.
Пример: исследование психики человека или влияние лекарства на организм мы воздействуем только на входы и делаем выводы на основании наблюдений за выходами в сигнал времени для пользователя, т.к. каждые часы показывают состояние своего датчика, то их показания постепенно расходятся. Выход состоит в синхронизации всех часов по показаниям некоего эталона времени (сигналы «точного времени» по радио). Включать эталон в состав часов как системы или рассматривать каждые часы как подсистему в общей системе указания времени?
Модель свойства системы. Элемент, подсистем, причины построения разных моделей разными экспертами
Система есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как единое целое.
Свойство, которое возникает из соединения частей – есть главный признак, сущность, суть явления. Понятие о явлении – это, в первую очередь, представление о сущности явления, о главном признаке явления, о свойстве порожденном в данной системе.
Например, телевизоры и автомобили бывают разными: маленькими и большими, хорошими и не очень, собранными по разным схемам из разных деталей. Но все они обладают некоторым отличительным свойством: телевизор – это явление, которое принимает телесигналы и воспроизводит телеизображение, а автомобиль – это “повозка, которая сама ездит”.
Составить понятие о явлении, значит: указать на существование явления – выделить явление, различить его; показать устройство явления; доказать взаимосвязи этого явления с другими, т.е. определить место этого явления в иерархии явлений.
Иерархия, вложенность явлений возникает оттого, что в явлениях – надсистемах задействуются свойства явлений-подсистем, порожденные их целостностью. Всякое свойство явления порождается на некотором уровне иерархии явлений, поэтому изучая явления необходимо различать свойства, унаследованные от составляющих частей и свойства, порожденные целостностью явления.
Множественность моделей систем
В основе моделирования лежит теория подобия, которая утверждает, абсолютное подобие может иметь место лишь при замене объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы достаточно хорошо отображало исследуемую строну функционирования объекта. Классификация видов моделирования приведена на рис. 1.1.
По степени полноты модели они делятся на полные, неполные и приближенные. Полные модели идентичны объекту во времени и пространстве. Для неполного моделирования эта идентичность не сохраняется. В основе приближенного моделирования лежит подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем.
В зависимости от характера изучаемых процессов в системе виды моделирования подразделяются на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает процессы, в которых предполагается отсутствие случайных воздействий. Стохастическое моделирование учитывает вероятностные процессы и события. Статическое моделирование служит для описания поведения объекта в фиксированный момент времени, а динамическое – для исследования объекта во времени. Дискретное, непрерывное и дискретно-непрерывное моделирования используются для описания процессов, имеющих изменение во времени. При этом оперируют аналоговыми, цифровыми и аналого-цифровыми моделями.
В зависимости от формы представления объекта моделирование классифицируется на мысленное и реальное. Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуации микромира).
Мысленное моделирование реализуется в виде наглядного, символического и математического. При наглядном моделировании на базе представлений человека о реальных объектах создаются наглядные модели, отображающие явления и процессы, протекающие в объекте. В основу гипотетического моделирования закладывается гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделирования используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговое моделирование основывается на применении аналогий различных уровней. Для достаточно простых объектов наивысшим уровнем является полная аналогия. С усложнением системы используются аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта. Макетирование применяется, когда протекающие в реальном объекте процессы не поддаются физическому моделированию либо могут предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.
| Моделирование систем |
| Приближенное |
| Полное |
| Неполное |
| Детерминированное |
| Стохастическое |
| Статическое |
| Динамическое |
| Дискретное |
| Дискретно-непрерывное |
| Непрерывное |
| Мысленное |
| Реальное |
| Математическое |
| Натурное |
| Наглядное |
| Символическое |
| Физическое |
| Рис. 1.1. Виды моделирования систем |














Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков и символов. В основе языкового моделирования лежит некоторый тезаурус, который образуется из набора входящих понятий, причем этот набор должен быть фиксированным. Между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус – словарь, который очищен от неоднозначности, т. е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову может соответствовать несколько понятий. Если ввести условное обозначение отдельных понятий, т. е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий – составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.
Математическое моделирование – это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т. е. построена математическая модель. Исследование математической модели позволяет получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения. Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т. д.) или логических условий. Аналитическая модель исследуется следующими методами: аналитическим, когда стремятся получить в общем виде явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы; численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных; качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
В настоящее время распространены методы машинной реализации исследования характеристик процесса функционирования БС. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм.
При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод исследования БС, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.
В имитационном моделировании различают метод статистического моделирования и метод статистических испытаний (Монте-Карло). Если результаты, полученные при воспроизведении на имитационной модели, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей обработкой информации. Поэтому целесообразно в качестве метода машинной реализации имитационной модели использовать метод статистического моделирования. Первоначально был разработан метод статистических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название метода Монте-Карло). Затем этот прием стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т. е. появился метод статистического моделирования.
Метод имитационного моделирования применяется для оценки вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть положено в основу структурного, алгоритмического и параметрического синтеза БС, когда требуется создать систему с заданными характеристиками при определенных ограничениях. Система должна быть оптимальной по некоторым критериям эффективности.
Комбинированное (аналитико-имитационное) моделирование позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей производится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это, возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели. Такой подход позволяет охватить качественно новые классы систем, которые не могут быть исследованы с использованием только аналитического или имитационного моделирования в отдельности.
Информационное моделирование (часто называемое кибернетическим) связано с исследованием моделей, в которых отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируются некоторые связи между выходами и входами. Таким образом, в основе информационных (кибернетических) моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести данную функцию на имитационной модели, причем на совершенно другом математическом языке и, естественно, иной физической реализации процесса.
Структурно-системное моделирование базируется на некоторых специфических особенностях структур определенного вида, используя их как средство исследования систем или разрабатывая на их основе с применением других методов формализованного представления систем (теоретико-множественных, лингвистических и т. п.) специфические подходы к моделированию.
Структурно-системное моделирование включает:
методы сетевого моделирования;
сочетание методов структуризации с лингвистическими (языковыми);
структурный подход в направлении формализации построения и исследования структур разного типа (иерархических, матричных, произвольных графов) на основе теоретико-множественных представлений и понятия номинальной шкалы теории измерений.
Ситуационное моделирование основано на модельной теории мышления, в рамках которой можно описать основные механизмы регулирования процессов принятия решений. В основе модельной теории мышления лежит представление о формировании в структурах мозга информационной модели объекта и внешнего мира. Эта информация воспринимается человеком на базе уже имеющихся у него знаний и опыта. Целесообразное поведение человека строится путем формирования целевой ситуации и мысленного преобразования исходной ситуации в целевую. Основой построения модели является описание объекта в виде совокупности элементов, связанных между собой определенными отношениями, отображающими семантику предметной области. Модель объекта имеет многоуровневую структуру и представляет собой тот информационный контекст, на фоне которого протекают процессы управления. Чем богаче информационная модель объекта и выше возможности ее манипулирования, тем лучше и многообразие качество принимаемых решений при управлении.
При реальном моделировании используется возможность исследования характеристик либо на реальном объекте целиком, либо на его части. Такие исследования проводятся как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т. д.). Реальное моделирование является наиболее адекватным, но его возможности ограничены. Например, проведение реального моделирования АСУП требует, во-первых, наличия такой АСУ и, во-вторых, проведения экспериментов с управляемым объектом, т. е. предприятием, что в большинстве случаев невозможно.
Натурным моделированием называют проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. Натурный эксперимент подразделяется на научный эксперимент, комплексные испытания и производственный эксперимент. Научный эксперимент характеризуется широким использованием средств автоматизации проведения, применением весьма разнообразных средств обработки информации, возможностью вмешательства человека в процесс проведения эксперимента. В соответствии с этим появилось новое научное направление – автоматизация научного эксперимента и новая специализация в рамках специальности АСУ – АСНИ (автоматизированные системы научных исследований и комплексных испытаний). Одна из разновидностей эксперимента – комплексные испытания, когда вследствие повторения испытаний объектов в целом (или больших частей системы) выявляются общие закономерности о характеристиках качества, надежности этих объектов. В этом случае моделирование осуществляется путем обработки и обобщения сведений о группе однородных явлений. Наряду со специально организованными испытаниями возможна реализация натурного моделирования путем обобщения опыта, накопленного в ходе производственного процесса, т. е. можно говорить о производственном эксперименте. Здесь на базе теории подобия обрабатывают статистический материал по производственному процессу и получают его обобщенные характеристики. Необходимо помнить про отличие эксперимента от реального протекания процесса. Оно заключается в том, что в эксперименте могут появиться отдельные критические ситуации и определиться границы устойчивости процесса. В ходе эксперимента вводятся новые факторы и возмущающие воздействия в процесс функционирования объекта.
Другим видом реального моделирования является физическое, отличающееся от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды, и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени или рассматриваться без учета времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, фиксируемые в некоторый момент времени. Наибольшие сложность и интерес с точки зрения корректности получаемых результатов представляет физическое моделирование в реальном масштабе времени.