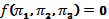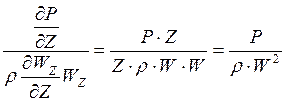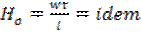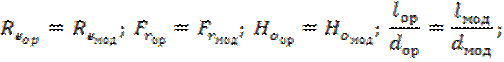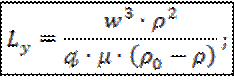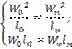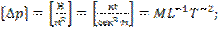что означает подобие начальных условий

19.10.202329.06.2023 admin 0 Comments

Подобие граничных и начальных условий

При исследовании какого-либо объекта или технологического процесса составляют систему дифф. Уравнений, которые описывают этот процесс на основе одного или нескольких физических законов.

Эта система описывает процесс и устанавливает связь между пространственно-временными изменениями физических величин. Сами по себе эти физические величины характеризуют процесс в общем виде.

Чтобы из системы дифф. Уравнений и целого ряда процессов выделить один конкретный, необходимо ограничить систему дифуров определенными условиями.

Для ограничения нужно:

— задать распределение в пространстве или в объеме важных для данного объекта знач. Факторов в начальный момент времени

— задать взаимоотношения с окружающей средой на границах систем (равентсво скорости потока = 0 у стенок трубопровода).

Граничные условия бывают 4 родов:

I рода имеют место быть если зависимость изменения температуры задана в виде функции в интервале времени.

II рода задаются тепловым потоком

III рода соответствуют зависимости температуры стенки объекта от температуры среды

IV рода – граничные условия задаются при модкор. Среды

Подобие граничных и начальных условий соблюдается при подобии геометрических, физических и временных величин.

Теоремы подобия

Практическое применение теорий подобия к экспериментальному и теоретическому исследованию процессов основано на трех теоремах подобия

Теорема Ньютона – Бертрана

Подобные явления характеризуются численно равными критериями подобия или у подобных явлений критерии подобия равны 1.

Теорема Бэкингема – Федермана

Любая зависимость между физическими величинами, характеризующими явление или процесс, может быть представлена в виде взаимной зависимсти между критериями подобия.

Теорема Кирпичева – Гухмана (обратная первой)

Подобны те явления или системы, которые описываются одинаковыми уравнениями связи, и условия однозначности которых подобны.

Теорема ОСНОВНАЯ Бэкингема (П-теорема)

Первые 3 теоремы формулируют необходимость и достаточность условий для рассмотрения подобия явлений и процессов.

Всякое уравнение, связывающее между собой n физических величин, среди которых m величин обладают независимыми размерностями, может быть преображено к уравнению, связывающему (n-m) безразмерных комплексов (критериев П и симплексов, состоящих из этих величин).

Метод анализа размерностей и основные критерии подобия

𝜋-теорема широко используется при проведении экспериментальных исследований, так как она позволяет находить связь не между отдельными физическими величинами, а между их безразмерными соотношениями 𝜋. Каждое из этих соотношений составляется по определенному закону.

Метод анализа размерностей

Позволяет выражать функциональную зависимость для любого процесса в виде уравнения связи между ними. Это уравнение связи строго определяется числом безразмерных комплектов, которые состоят из физических величин со своей размерностью.

Метод анализа размерностей базируется на двух допущениях:

— из практических данных известно от каких параметров процесса и переменных зависит функция или рассматриваемая физическая величина

— связь между всеми необходимыми для данного процесса физическими величинами выражается в виде степенного многочлена

Для того чтобы использовать степенной многочлен на практике нужна степенная однородность. В уравнение подставляют размерности входящих в него величин, и тем самым достигается размерная однородность. Размерная однородность обеспечивает независимость уравнения от переменных, которые имеют каждая свою единицу измерения. Это называется инвариантностью уравнения.

Пример:

Рассмотрим ламинарное движение жидкости в прямой трубе. Допустим, что мы не знаем закона движения этой жидкости, но имеем ряд практических данных и можем предположить, что перепад давления в начале и в конце трубы зависит от

Функция этого степенного уравнения имеет размерную однородность. Каждый член этого уравнения имеет свою единицу измерения и чтобы сделать это уравнение инвариантным мы должны привести его к инвариантному виду, поэтому

Для достижения инвариантности добавляем безразмерный постоянный коэффициент В.

Размерная однородная система, которая состоит из размерных величин, может быть заменена безразмерной системой. Для этого составляется матрица величин, и мы выражаем все размерности через 3 основные (m, l, t)

После всех математических преобразований уравнения мы получаем 3 основных комплекса безразмерных

– критерий Эйлера;

— критерий Рейнольдса;

— геометрический симплекс или инвариантное постоянство.

Запишем уравнение в критериальной форме

Для перехода от функциональной зависимости к критериальной форме используют критерии подобия. Эти критерии применяют для описания гидравлических, механических и прочих процессов.

Источник

Большая Энциклопедия Нефти и Газа

Подобие начальных условий принимается во внимание для переходных процессов. [1]

Подобие начальных условий означает, что в тот момент, когда начинается изучение процесса, соблюдается подобие всех физических величин, которые характеризуют процесс. [2]

Подобие начальных условий означает, что в момент, когда начинается изучение процесса ( начальный момент), соблюдается подобие полей всех физических величин, характеризующих процесс. [3]

Подобие начальных условий означает, что в момент, когда начинается изучение процесса ( начальный момент), соблюдается подобие полей всех физических величин во всем объеме, охваченном изучаемым процессом. [4]

При соблюдении подобия начальных условий коэффициент k в различных точках струи является величиной постоянной, не зависящей от координат и скорости. [5]

Теперь ясно, что подобие начальных условий означает подобие полей всех переменных в начальный момент процесса. [6]

Теперь для нас очевидно, что подобие начальных условий означает подобие нолей все переменных в начальный момент процесса. [7]

Необходимо, чтобы соблюдалось геометрическое подобие аппарата и модели и подобие начальных условий распределения скорости на входе в зернистый слой. [8]

Оно подобно дифференциальному уравнению ( VI 1.2) и при подобии начальных условий приводит к подобным же решениям. [9]

Условие подобия поля скоростей по контрольным сечениям потока носит название кинематического подобия. Подобие начальных условий необходимо принимать во внимание только для переходных процессов. [11]

Если амортизирующее крепление не обладает трением ( R 0), то п О, К Я, и дифференциальные уравнения ( VII. При одинаковых закономерностях изменения во времени их правых частей и при подобии начальных условий все они приведут к подобным решениям. [12]

В таких случаях для нахождения зависимостей, характеризующих взаимосвязь переменных физических величин, которые влияют на ход процесса, проводят экспериментальное исследование. Для обобщения результатов экспериментальных исследований и распространения пределов их применения на более широкую группу подобных процессов используют методы теории подобия. Подобие начальных условий означает, что в момент, когда начинается исследование процесса, соблюдается подобие полей всех физических неременных величин, характеризующих процесс. [13]

В таких случаях для нахождения зависимостей, характеризующих взаимосвязь переменных физических величин, влияющих на ход процесса, проводят экспериментальное исследование. Для обобщения результатов экспериментальных исследований и для расширения пределов их применения в более широкой группе подобных процессов используют методы теории подобия. Подобие начальных условий означает, что в момент, когда начинается исследование процесса, соблюдается подобие полей всех физических переменных величин, характеризующих процесс. [14]

Источник

Очевидно, что и бесконечно малые приращения (дифференциалы) также будут связаны масштабами

(04)

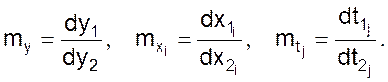
Обратим внимание на последний масштаб m_pj в выражении 2.3. Найдем отношение двух производных

(05)

(06) Если учесть, что

(07)

(08)

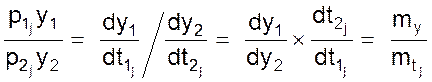
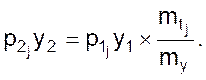
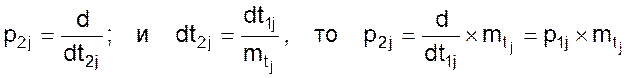
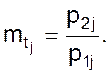
Но полученное отношение не, что иное, как величина обратная масштабу операторов m_pj.

(09)

(10)

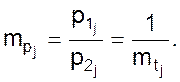
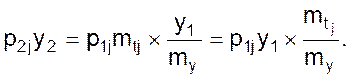
Вторая производная 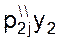по тому же принципу может быть заменена сходственной переменной

(11)

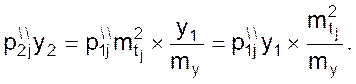
Все изложенное распространяется на частные и смешанные производные.

Как и в предыдущем случае, масштабные уравнения, которые позволяют определить масштабы, можно получить двумя способами: способом подстановки и при помощи критериев подобия.

Сущность способа подстановки состоит:

■ в замене переменных в одном из сходственных уравнений сходственными переменными второго уравнения с помощью масштабных коэффициентов;

■ в обеспечении тождественности промежуточного уравнения и второго сходственного уравнения;

■ в получении масштабных уравнений как условий тождественности промежуточного уравнения и второго сходственного уравнения.

Сущность способов критерия подобия состоит в следующем:

■ сходственным уравнениям придается безразмерная форма;

■ определяются критерии подобия;

■ масштабные уравнения получают приравниванием единице отношения сходственных критериев подобия.

3.1. Четвертое условие подобия.

Обратившись к ситуации, когда объекты описываются уравнениями общего вида, мы предположили, что три ранее сформулированных условия подобия остаются в силе. При этом мы рассматривали случай, когда каждое из сходственных уравнений имеет единственное решение. Однако такое положение сохраняется далеко не всегда. Например, к математическим описаниям объектов, имеющим не единственное решение, помимо уравнений общего вида относятся дифференциальные уравнения, в том числе и в частных производных.

В случае если уравнение, предназначенное для описания объекта, имеет несколько решений, то ввиду того, что состояние реального физического объекта всегда однозначно, требуется указать, какое решение соответствует действительности.

Условия, конкретизирующие одно решение из нескольких, называют условиями однозначности.

(12)

(13)

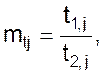
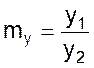
связывает только значения сходственных однозначных функций

■ в случае подобия объектов их однозначные состояния должны определяться сходственными однозначными функциями. Если данное условие не соблюдается, подобие объектов невозможно, несмотря на очевидное подобие сходственных уравнений;

■ в случае если математические описания объектов представляют обыкновенные дифференциальные уравнения, условиями однозначности являются начальные условия.

(14)

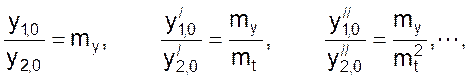
что означает подобие начальных условий (в данном случае условий однозначности).

Аналогично, подобие начальных условий необходимо и при описании объектов дифференциальными уравнениями в частных производных.

Таким образом, к трем условиям подобия, сформулированным выше, должно быть добавлено четвертое условие подобия – сходственность условий однозначности решений сходственных уравнений, содержащихся у математических описаниях объектов, и пропорциональность содержащихся в них сходственных переменных.

3.2. Пятое условие подобия.

(15)

(16)

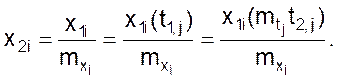
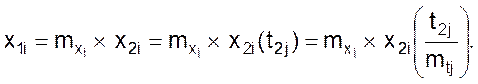
Из изложенного вытекает пятое условие подобия – сходственность заданных функций, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в этих функциях сходственных переменных.

Итак, для подобия двух объектов необходимо и достаточно:

1. Иметь сходственность математических описаний;

2. Иметь связь сходственных переменных масштабами;

3. Иметь выбор масштабов согласно масштабным уравнениям;

4. Иметь сходственность условий однозначности решений сходственных уравнений, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в них сходственных переменных.

5. Иметь сходственность заданных функций, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в этих функциях сходственных переменных.

4.1. Исходные данные, необходимые для подобного моделирования.

Для создания подобного объекта-модели необходимо располагать исходными данными, к которым относятся:

1. Математическое описание оригинала;

(17)

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.

Основы теории подобия

1. Сущность теории подобия. Физическое и математическое моделирование.

Расчёт аппаратов может производиться несколькими методами:

1. Наиболее точный и предпочтительный путь изучения и расчёта процессов — теоретический:

а) составление на основе общих законов физики и химии математических зависимостей;

б) составление дифференциальных уравнений, полностью описывающих процесс и их решение.

Однако дифференциальное уравнение описывает не единичный процесс, а бесконечное множество одинаковых процессов.

Чтобы описать единичный, конкретный процесс, нужно задать условия, в виде конкретных численных значений:

К условиям однозначности относят:

1) Геометрические условия, характеризующие форму и размеры аппаратуры, в которой протекает процесс.

2) Физические характеристики системы в виде физических констант или уравнений, выражающих зависимость свойств и различных параметров.

3) Граничные условия, описывающие значения всех существующих параметров на границах системы с окружающей средой.

4) Начальные условия в момент времени, принимаемого за начало отчёта.

Например, при движении жидкости в трубе;

-геометрические условия 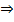диаметр и длина трубы;

-физические свойства жидкости

-граничные условия (например,

-начальные условия в момент

Таким образом, для расчёта конкретного процесса дифференциальные уравнения интегрируются в пределах, установленных условиями однозначности.

Однако, интегрирование уравнений переноса вследствие их сложности представляет большие трудности. Обычно решение уравнений становится возможным только при их упрощении и использовании методов численного интегрирования с применением ЭВМ. Эти методы лежат в основе математического моделирования, которое включает в себя:

1) Описание конкретного процесса в виде его математической модели (системы уравнений);

2) Решение уравнений на ЭВМ;

3) Установление адекватности математической модели реальному процессу.

Использование ЭВМ позволяет проводить расчеты многократно, при различных исходных данных (условиях однозначности); При этом процессы можно исследовать в широком диапазоне изменения параметров и определить оптимальные условия.

Важным достоинством метода математического моделирования является возможность изучения сложных процессов без создания опытных установок. и возможность исследования режимов, которые трудно реализовать по условиям ТБ или экономическим соображениям.

Недостаток метода 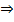трудность получения адекватного математического описания ввиду большой сложности реальных процессов и влияние различных явлений переноса друг на друга. Приходится пренебрегать некоторыми факторами, вносить поправочный коэффициент.

Многие процессы характеризуются большим числом переменных и настолько сложны, что зачастую удаётся дать лишь математическую формулировку задачи и установить условия однозначности. Полученные таким образом дифференциальные уравнения не могут быть решены.

Наиболее плодотворным является осуществление таких экспериментов, которые позволяют обобщить результаты опытов на определённую группу подобных процессов. Это достигается при использовании теории подобия.

Основы теории подобия

Теория подобия является учением о методах научного обобщения результатов физических экспериментов.

Она указывает, как нужно ставить опыты и обрабатывать полученные данные, чтобы при проведении относительно небольшого числа экспериментов их можно было бы распространить на процессы, протекающие в условиях, отличающихся от условий эксперимента.

Таким образом, вместо промышленных объектов изучаются малые модели аппаратов, обработка полученных результатов методами теории подобия позволяют распространить полученные экспериментальные данные на большие промышленные объекты.

Это физическое моделирование, когда физическая сущность процесса на модели и в натуре одна и та же (меняются только масштабы установки, используемые вещества и т.д.).

Наилучший путь состоит в комбинировании физического и математического моделирования; роль последнего непрерывно возрастает с прогрессом вычислительной техники и прикладной математики.

Условия и теоремы подобия.

Условия однозначности позволяют выделить из класса единичные явления. Однако в пределах класса явления очень разнообразны (движение жидкости), поэтому можно из класса выделить группы подобных явлений. Это лишь часть явлений данного класса, на которую можно распространить данный единичный опыт.

Для группы подобных явлений (чтобы её выделить) условия однозначности строят по особому правилу.

Рассмотрим условия подобия, соответствующие особому построению условий однозначности.

2.Условия и теоремы подобия.

Важным моментом является выделение из класса явлений группы подобных явлений ( уравнение Новье-Стокса: вязкая жидкость под действием разности давлений).

Явления называются подобными, если для них постоянны отношения сходственных величин.

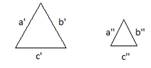
Например: из класса плоских геометрических фигур (треугольники, многоугольники) можно выделить группы подобных фигур треугольников,

сходственные размеры которых параллельны, а отношения их постоянны:

Подобные фигуры будут отличаться только масштабом.

Однако при протекании физических процессов соблюдение геометрических пропорций является необходимым, но недостаточным условием. Должны быть подобны все основные физические величины, влияющие на процесс, как во времени, так и в пространстве.

Сформулируем необходимые условия подобия:

Рассмотрим в качестве примера течение жидкости в двух трубах:

1.Геометрические подобия соблюдаются при равенстве отношений всех сходственных линейных размеров натуры и модули:

где: 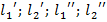— пути, проходимые сходственными частицами от входа в натуру и модель до произвольных сходственных точек.

константа геометрического подобия, характеризует соотношение между геометрическими параметрами подобных систем и позволяющая перейти от размеров одной системы к другой.

2.Временное подобие соблюдается если отношение между сходственными интервалами времени процесса сохраняется постоянное значение (сходственный интервал времени, это интервал в течении которого завершаются аналогичные стадии процесса).

В нашем случае: сходственные частицы, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых постоянно:

где: – время прохождения всей трубы.

— время прохождения сходственными точками подобных путей.

константа временного подобия (гемохронности)

Если говорят о синхронности процессов.

Пример: загрузка, нагревание, перемещение, охлаждение, выгрузка.

3.Подобие физических величин соблюдается, если для сходственных точек натуры и модели, размещённых подобно в пространстве и времени (т.е. соблюдается геометрическое и временное подобие), отношение физических свойств является величинами постоянными.

Например:

4.Подобие начальных и граничных условий соблюдается, если отношение основных параметров в начале процесса и на границе натуры и модели являются соответственно величинами постоянными, т.е. если для начальных и граничных условий соблюдаются геометрические, временные и физические подобия, как и для других сходственных точек.

Таким образом, подобие условий однозначности для группы подобных явлений включает в себя геометрическое, временное подобие, а также подобие физических величин, и подобие начальных и граничных условий.

Константы подобия и др. постоянны для разных сходственных точек подобных систем, но численно могут отличаться друг от друга. В константах подобия отношения величин можно заменить отношениями приращений:

Например:

Константы подобия численно отличаются друг от друга.

Основные положения теории подобия обобщаются теоремами подобия. Константы подобия Кл, Кч, Кр и др. должны определённым образом согласовываться друг с другом. Это устанавливается теоремами подобия.

1. теорема Ньютона-Бертрана (теорема о необходимых условиях подобия):

Подобные явления характеризуются численно равными критериямиподобия.

Для пояснения понятия «критерий подобия» рассмотрим простейший пример:

Выделим в двух подобных системах две подобно движущиеся частицы массой m1 и m2. Пусть на частицу m1 действует сила f1, создающая ускорение

Дифференциальное уравнение движения:

На частицу

При подобном движении для сходственных точек натуры и модели можно записать:

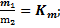
Следствием подобия этих переменных является подобие сил:

Подставим эти значения в 1-ое уравнение:

;

или: ;

Для подобных процессов уравнения (сравним с уравнением 2) должны быть тождественны следовательно:

индикатор подобия.

У подобных процессов (систем) индикатор подобия равен 1, т.е. выбор констант подобия не произволен, можно выбрать только три из них, а значение четвёртого будет определяться из уравнения.

Заменим константы подобия через их первоначальные значения:

Комплекс =Ne критерий Ньютона, характеризующий отношение действующих на частицу силы к силе инерции. Он используется в случае механического подобия.

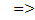
В константах подобия отношения величин можно заменить отношениями приращений:

Например: =

Основные положения теории подобия обобщается теоремами подобия. Константы подобия , и др. должны определённым образом согласовываться друг с другом. Это устанавливается теоремами подобия.

Все критерии подобия представляют собой безразмерные комлексы, имеющие строгий физический смысл, и являются мерой соотношения между какими-то двумя противоположными эффектами.

Чаще всего, критерии подобия находят, деля одну часть дифференциального уравнения, описывающего данный процесс, на другую и отбрасывая при этом знаки математических операторов.

Первая теорема подобия указывает, какие величины следует измерять при обобщении результатов опытов – те величины, которые входят в критерий подобия.

2-я теорема Бэкингема-Федермана:

Решение любого дифференциального уравнения, описывающего данный процесс, может быть представлено в виде зависимости между критериями подобия:

Таким образом, решение дифференциального уравнения может быть представлено в общем виде зависимостью:

f ( ₁; ₂; ₃… _n) = 0;

где: — критерий подобия.

Такие зависимости называются критериальнымиуравнениями.

Необходимо отметить, что различают определяющие и определяемые критерии подобия.

а) Определяющие критерии составлены только из величин, необходимых для однозначной характеристики процесса. Однозначно выделяют из класса одно конкретное явление.

б) Определяемые критерии включают в себя также величины, которые не могут быть заранее вычислены.

Какой из критериев является определяемым, зависит от формулировки задачи.

Например: если задана форма трубы (d;l),

физические свойства жидкости,

распределение скоростей у входа в трубу и у её стенок (начальные и граничные условия)

то совокупность этих условий однозначно определяет перепад давлений между любыми точками трубы ( ).

Следовательно, критерий подобия, в который, кроме условий однозначности, входят величина от них зависящая, будет определяемым.

Вторая теорема подобия указывает, как обрабатывать результаты опытов, полученные на лабораторных моделях: Их надо представлять в виде функциональной зависимости между критериями подобия (то есть в виде критериальных уравнений).

Я теорема Кирпичёва-Гухмана

Она определяет необходимые и достаточные условия подобия.

Подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.

Подобию условий однозначности отвечает равенство определяющих критериев.

Равенство определяющих критериев является необходимым условием подобия.

Равенство определяемых критериев является следствием подобия

Исследование процессов методом теории подобия должно состоять из следующих этапов:

1) Составив дифференциальные уравнения (и установив условия однозначности), проводят подобное преобразование этих уравнений и находят критерии подобия.

2) Опытным путём на моделях устанавливают конкретный вид зависимости между критериями подобия, то есть строят критериальное уравнение.

Обычно представляют:

т.е. в виде степенных зависимостей. При этом, численные показатели степеней и коэффициент А определяются экспериментально на модели.

Необходимо отметить двоякую роль критериев подобия:

1)Значения критериев обеспечивают количественный перенос результатов опыта на оригинал (численное равенство критериев);

2)На основе критериев определяют, какой должна быть модель, чтобы обеспечит условия моделирования.

Пример: течение жидкости по трубопроводу:

Форма модели определяется условиями геометрического подобия.

Для подобия необходимо:

;

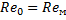
Для одной жидкости ( ):

Таким образом, скорость жидкости в модели должна быть обратно пропорциональна её размеру, т.е. чем меньше модель, тем больше скорость.

Гидродинамическое подобие

Запишем уравнение Навье-Стокса для одномерного движения не-сжимаемой жидкости, то есть когда W _z меняется только в направлении оси Z:

В этом уравнении левая часть учитывает действие силы инерции,

а в правой части уравнения учитывает силу тяжести,

слагаемое учитывает силы гидростатического давления, а

силы вязкого трения.

По первой теореме

Критерии гидродинамического подобия получим путём деления каждого члена диф. уравнения на один из других, отбрасывая при этом знаки математических операторов (плюс, минус, дифференцирования):

1).

Это критерий Эйлера:

Eu =
Физический смысл: Он выражает меру соотношения силы гидростатического давления к силам инерции в подобных потоках.

Этот критерий определяемый, равенство его в подобных системах является следствием подобия.

То полученное выражение называется критерием Рейнольдса:
Re = .
Физический смысл этого критерия : Он выражает меру отношения инерционных сил и вязкостных сил в подобных потоках.

Это определяющий критерий, его равенство является необходимым условием подобия.

Полученное выражение называется критерием Фруда:
Fr =

Физический смысл: это определяющий критерий, который выражает меру отношения инерционных сил и сил тяжести в подобных потоках.

4.

Полученное выражение называется критерием гомохронности:

Физический смысл: это определяющий критерий и выражает меру отношения локального изменения инерционных сил к конвективному, и учитывает неустановившейся характер движения в подобных потоках.

Применяется только при неустановившемся режиме;

Для установившихся процессов и критерий выпадает.

Это определяющий критерий, неустановившиеся процессы могут быть подобны лишь в том случае, если подобные изменения всех переменных в сходственных точках будут проходить в интервалы времени, определяемые требованием:

Решение уравнения Навье-Стокса можно представить в виде функциональной зависимости между полученными критериями подобия:

В ряде случаев эта зависимость должна быть дополнена параметрическими критериями 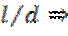это отношение одноименных величин (симплекс геометрического подобия) = idem для сходных точек подобных систем.

Все критерии, кроме , являются определяющими, т.к. составлены исключительно из величин, входящих в условия однозначности.

В критерий входит искомая величина , значение которой при движении жидкости по трубе полностью определяется формой и размерами , физическими свойствами жидкости и распределением скоростей на входе в трубу и её на выходе (начальные и граничные условия).

По 3 теореме

Следовательно, для подобия необходимо и достаточно:

Следствием выполнения этих условий будет:

Из критериального уравнения определяют 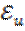, а из него – потерю напора при движении жидкости.

Зависимость представляют обычно в виде степенной:

Показатели степеней m ; n ; q ; p и A определяются опытным путём.

В ряде случаев критериальное уравнение упрощается, когда процесс не зависит от какого-либо критерия, т.е. является автомодельным по нему:

1. Например, в случае установившегося движения исключается критерий гомохронности:

2. При установившемся движении жидкости в горизонтальной трубе влияние собственного веса (силы тяжести) на перепад давления мало и можно записать:

Но при истечении жидкостей критерий Fr необходимо учитывать.

Необходимо отметить, что число критериев подобия, зависимость между которыми заменяет дифференциальное уравнение, на единицу меньше числа членов этого уравнения (например, если членов уравнения 5, число критериев 5-1 = 4).

К этому присоединяются параметрические критерии, число которых зависит от числа пар одноименных величин (одноименные 2 x,z; одна пара = один параметрический критерий).

Производные критерии подобия

В ряде случаев какая-либо физическая величина, входящая в критерий подобия, не может быть экспериментально определена или вычислена.

Например, при естественной конвекции, обусловленной разностью плотностей жидкости, отсутствует русло потока, поэтому не может быть определена его скорость. В этом случае скорость исключают путём деления двух критериев в которые эта скорость входит, получая так называемые производные критерии подобия, составленные из основных.

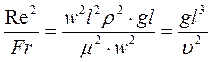
Полученное выражение называется производным критерием Галилея:

Физический смысл: он характеризует соотношение сил тяжести и сил трения в свободных потоках.

2) Поскольку причиной свободной конвекции является разность плотностей, то эту разность необходимо учитывать (в виде параметрического критерия):

Ar = .

Полученное выражение называется производным критерием Архимеда:

Физический смысл :Он выражает меру отношения сил тяжести, подъёмной силы к силе трения.

3) В тех случаях, когда неизвестной величиной является линейный размер (например, диаметр частиц пыли), используют другой производный критерий подобия (исключая линейный размер):

Полученное выражение называется производным критерием Лященко:

Физический смысл: он является мерой соотношения сил инерции, тяжести, вязкости и подъёмной силы.

Автомодельность

При моделировании многих процессов химической технологии не удаётся соблюдать полное подобие – равенства всех определяющих критериев для модели и оригинала, как этого требует -я теория подобия.

При истечении жидкости процесс зависит от критериев 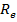и . Для полного подобия требуется:

1. Если 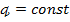и жидкость одна и та же :

Эта система имеет единственное решение:

2.Используем другую жидкость, но оставим условие :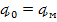

Если , то т.е. в 8 раз меньше чем у воды (таких жидкостей нет).

3.Изменяем , например, составим модель на центрифугу; но оставим условие:

При т.е. это находится за пределами технических возможностей.

Практически оказалось невозможным построить модель, подобную оригиналу. При достаточном большом числе подобия задача становится нереальной.

Это обстоятельство воспрепятствовало широкому применению методов подобия для моделирования химических реакций. Изменяются критерии Дамкелера, Дьяконова для реакторных процессов (большая сложность, т.к. влияют теплообмен, массообмен, гидродинамика) т.е. большое число факторов.

Когда удаётся выделить лимитирующую стадию, влиянием большинства факторов можно пренебречь, и создание модели (хотя и редко) на основе теории подобия становится возможным.

В курсе ПАХТ это встречается часто, т.к. он построен на единой методической основе – теории подобия.

Если какой либо критерий не влияет на процесс, то процесс называется автомодельным по этому критерию. При этом соблюдается не полное подобие, а подобие лишь тех факторов, которые наиболее значительно влияют на данный процесс.

Автомодельность может наступать при изменении условий протекания жидкости. При больших 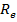сопротивление трубы не зависит от режима течения, а определяется шероховатостью стенок.

Метод анализа размерности

Для сложных процессов, зависящих от большого числа факторов, не всегда удаётся составить описывающие их дифференциальные уравнения, и следовательно, отсутствует возможность выделить критерий подобия подобным преобразованием дифференциального уравнения.

В таких случаях принимают метод анализа размерностей, позволяющий также получить критериальное уравнение.

В основу метода положена –теорема:

Общую функциональную зависимость, связывающую между собой n переменных величин при m основных единицах их измерения, можно представить в виде зависимости между (n-m) критериями подобия.

Положительные моменты: метод применяется, когда мало известно об явлении.

Отрицательные моменты: а) необходимо точно знать, какие параметры влияют на процесс;

б) нельзя сформировать условия однозначности и следовательно разделить критерии на определяющие и определяемые.

Пример: При исследовании установившегося течения жидкости найдено: