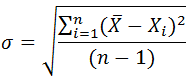что означает сигма в статистике
Что означает сигма в статистике
σ – греческая буква, принятая в статистике для обозначения среднеквадратического (или стандартного) отклонения. Используется для описания распределения наблюдений какой-либо характеристики вокруг среднего/целевого значения.
Стандартное отклонение рассчитывают по формуле:
где σ – стандартное отклонение, X̅ – среднее арифметическое всех наблюдений, Xi – величина i-вого наблюдения, а n – общее количество наблюдений.
σ-уровень также является показателем поведения процесса. В данном случае, количество σ, находящееся между средним значением и ближайшим пределом допуска, является бизнес-индикатором стабильности процесса и доли дефектной продукции.
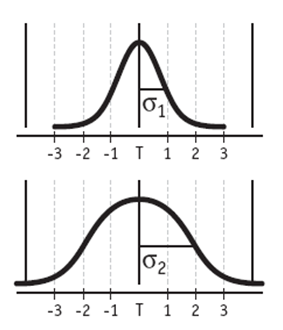
Если величина стандартного отклонения вырастет, к примеру, в два раза, то количество сигм, которое может поместиться на отрезке между целевым значением и ближайшим пределом допуска, соответственно, уменьшиться в два раза. При этом, доля произведенной продукции, характеристики которой находятся за пределами допуска спецификации, тоже вырастет – это означает, что количество дефектной продукции увеличится.
Что случиться если значение сигма уменьшиться?
Логично, что снижение величины стандартного отклонения, сопровождаемое повышением стабильности процесса, приведет к снижению доли дефектной продукции. Задача 6σ заключается в повышении качества продукции путем понижения значения σ, т.е. вариации процесса.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Стандартное отклонение
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
Однако, глядя на цифры, можно заметить:
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
5. Поделить на размер выборки (т.е. на n):
6. Найти квадратный корень:
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
Ещё расчёт дисперсии можно сделать по этой формуле:
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
Конспект курса «Основы статистики»
1. Введение
Способы формирования репрезентативной выборки:
Простая случайная выборка (simple random sample)
Стратифицированная выборка (stratified sample)
Групповая выборка (cluster sample)
Типы переменных:
непрерывные (рост в мм)
дискретные (количество публикаций у учёного)
Ранговые (успеваемость студентов)
Гистограмма частот:
Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.
Описательные статистики:
Меры центральной тенденции (узкий диапазон, высокие значения признака):
( используется для среднего значения из выборки, а для генеральной совокупности латинская буква
)
Свойства среднего:
Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.
Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.
Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.
Меры изменчивости (широкий диапазон, вариативность признака):
При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.
Дисперсия генеральной совокупности:
(среднеквадратическое отклонение генеральной совокупности)
(среднеквадратическое отклонение выборки)
Свойства дисперсии:
Квартили распределения и график box-plot

Нормальное распределение
Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.
Стандартизация
Правило «двух» и «трёх» сигм
Центральная предельная теорема
Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .
30″ alt=»SE = \frac
Доверительные интервалы для среднего
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).
Идея статистического вывода
2. Сравнение средних
T-распределение
Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).
Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от
«Форма» распределения определяется числом степеней свободы ().
С увеличением числа распределение стремится к нормальному.
t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.
Сравнение двух средних; t-критерий Стьюдента
Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.
Условия для корректности использования t-критерия Стьюдента:
Две независимые группы
Формула стандартной ошибки среднего:
Формула числа степеней свободы:
Формула t-критерия Стьюдента:
Переход к p-критерию:
Проверка распределения на нормальность, QQ-Plot
Однофакторный дисперсионный анализ
Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.
Группы:
Нулевая гипотеза:
Альтернативная гипотеза:
Среднее значение всех наблюдений:
Общая сумма квадратов (Total sum of sqares):
Показатель, который характеризует насколько высока изменчивость данных, без учёта разделения их на группы.
Число степеней свободы:
— Межгрупповая сумма квадратов (Sum of sqares between groups)
— Внутригрупповая сумма квадратов (Sum of sqares within groups)
F-значение (основной статистический показатель дисперсионного анализа):
При делении значения межгрупповой суммы квадратов на число степеней свободы, полученный показатель усредняется.
Поэтому формула F-значения часто записывается:
Множественные сравнения в ANOVA
Проблема множественных сравнений:
Поправка Бонферрони
Самый простой (и консервативный) метод: P-значения умножаются на число выполненных сравнений.
Критерий Тьюки
Критерий Тьюки используется для проверки нулевой гипотезы против альтернативной гипотезы
, где индексы
и
обозначают любые две сравниваемые группы.
Указанные сравнения выполняются при помощи критерия Тьюки, который представляет собой модифицированный критерий Стьюдента:
где — рассчитываемая в ходе дисперсионного анализа внутригрупповая дисперсия.
Многофакторный ANOVA
При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.
Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.
Условия применения двухмерного дисперсионного анализа:
Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.
Выборки должны быть независимыми.
Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.
Группы должны иметь одинаковый объем выборки.
АБ тесты и статистика
3. Корреляция и регрессия
Понятие корреляции
Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.
Принимает значения [-1, 1]
— показатель силы и направления взаимосвязи двух количественных переменных.
Знак коэффициента корреляции показывает направление взаимосвязи.
Коэффициент детерминации
— показывает, в какой степени дисперсия одной переменной обусловлена влиянием другой переменной.
Равен квадрату коэффициента корреляции.
Принимает значения [0, 1]
Условия применения коэффициента корреляции
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:
Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.
Распределения переменных и
должны быть близки к нормальному.
Число варьирующих признаков в сравниваемых переменных и
должно быть одинаковым.
Коэффициент корреляции Спирмена
Регрессия с одной независимой переменной
Уравнение прямой:
— (intersept) отвечает за то, где прямая пересекает ось y.
— (slope) отвечает за направление и угол наклона, образованный с осью x.
Метод наименьших квадратов
Формула нахождения остатка:
— остаток
— реальное значение
— значение, которое предсказывает регрессионная прямая
Сумма квадратов всех остатков:
Параметры линейной регрессии:
Гипотеза о значимости взаимосвязи и коэффициент детерминации
Коэффициенты линейной регрессии
Коэффициенты регрессии (β) — это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой.
Коэффициент детерминации
— доля дисперсии зависимой переменной (Y), объясняем регрессионной моделью.
— сумма квадратов остатков
— сумма квадратов общая
Условия применения линейной регрессии с одним предиктором
Линейная взаимосвязь и
Нормальное распределение остатков
Регрессионный анализ с несколькими независимыми переменными
Множественная регрессия (Multiple Regression)
Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависимую.
Требования к данным
линейная зависимость переменных
нормальное распределение остатков
проверка на мультиколлинеарность
нормальное распределение переменных (желательно)