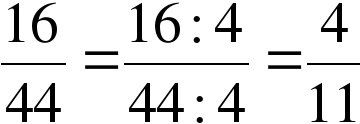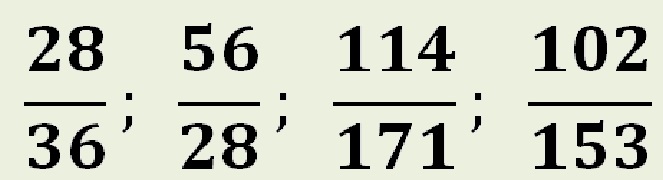что означает сократить дробь

Сокращение дробей. Что значит сократить дробь?

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.

Формула сокращения дробей основного свойства рациональных чисел.

Рассмотрим пример:
Сократите дробь \(\frac<9><15>\)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

Ответ: после сокращения получили дробь \(\frac<3><5>\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac<48><136>\).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

Правило сокращения дроби до несократимого вида.

Пример:
Сократите дробь \(\frac<152><168>\).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac<19><21>\) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac<44><32>\).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac<30><45>\).

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac<100><150>\).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

Получили несократимую дробь \(\frac<2><3>\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac<100><150>\) на 2.

Получили сократимую дробь \(\frac<50><75>\).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac<4><8>\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac<2><3>\) и \(\frac<8><12>\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac<8><12>\):

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) \(\frac<90><65>\) б) \(\frac<27><63>\) в) \(\frac<17><100>\) г) \(\frac<100><250>\)

Источник

Сокращение дроби.

Мы уже познакомились с основным свойством дроби (см. статью здесь). И знаем, как получить дробь, равную данной. Но сегодня мы поговорим о ДЕЛЕНИИ дроби на одно и то же число.

Деление числителя и знаменателя на одно и то же натуральное число называется СОКРАЩЕНИЕМ ДРОБИ. Но при этом – дроби остаются РАВНЫМИ.

Как сокращать дроби? Будем разбираться.

Итак, сокращение дроби – это действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Сокращение дроби выполняют для того, чтобы ее упростить.

Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же натуральное число, которое будет называться общим делителем.

Например, дана дробь 2/6.

На какие числа можно разделить 2? 2 делится на 1, 2. На какие числа можно разделить 6? 6 делится на 1, 2, 3, 6.

Но, мы знаем, что если дробь разделить на 1, то будет та же самая дробь. Поэтому на 1 не сокращают!

Теперь посмотрим на делители чисел 2 и 6. Сравним их:

Найдем одинаковые делители – это только число 2. Значит, мы можем разделить числитель и знаменатель нашей дроби только на 2.

Дробь 1/3 сократить нельзя.

Посмотрим на дробь 16/44. 16 делится на 2, 4, 8, 16. 44 делится на 2, 4, 11, 44. Одинаковые делители – 2, 4.

Разделим дробь на 2 — 16:2/44:2 = 8/22. Эту дробь можно еще сократить на 2. 8/22 = 8:2/22:2 = 4/11. Это очень долго, поэтому будем сокращать сразу на 4.

Дробь 4/11 сократить нельзя.

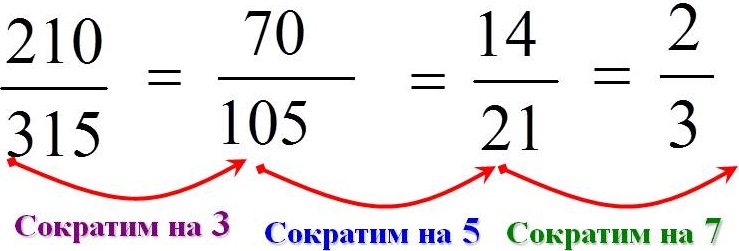
Рассмотрим дробь с большими числами: 210/315.

210 делится на 2, 3, 5, 7, 10, 30, 70, 105, 210.

315 делится на 3, 5, 7, 9, 15, 21, 63, 105, 315.

Общие делители: 3, 5, 7, 105. Будем сокращать дробь постепенно:

Мы видим, что если сокращать поочереди на все общие числители, начиная с меньшего, очень долго. Поэтому для удобства принято сокращать дробь сразу на больший числитель. Т.е. 210/315 = 210:105 / 315:105 = 2/3 Полученную дробь 2/3 сократить нельзя.

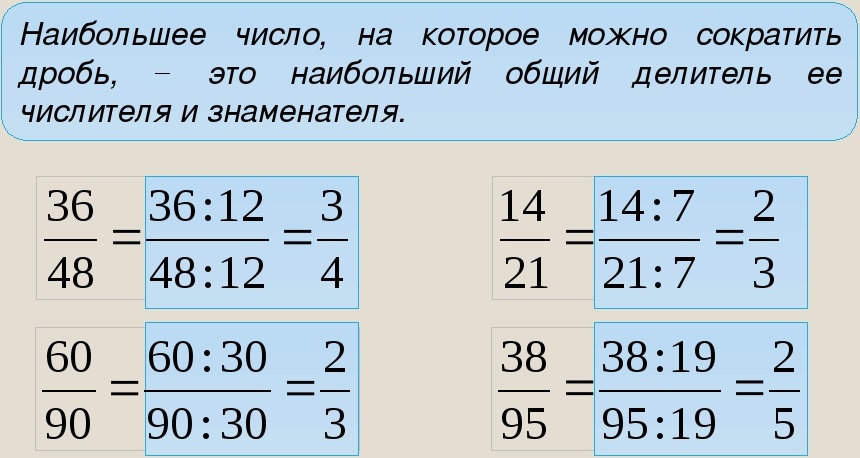
Наибольший общий делитель называют сокращенно — НОД.

Бывают случаи, когда общего делителя нет. Например, у дробей 3/59, 6/31, 11/23 и т.д. Тогда говорят о том, что эти дроби не подлежат сокращению.

Дроби, которые сократить НЕЛЬЗЯ называются НЕСОКРАТИМЫМИ, а числитель и знаменатель называют ВЗАИМНО-ПРОСТЫМИ.

Т.е. наша задача превратить любую дробь в несократимую. Итак, мы познакомились в двумя способами сокращения дробей:

Проверка: 28/36 – наибольший общий делитель (НОД) = 4, значит 28:4/36:4 = 7/9;

56/28 – НОД = 28, значит, 56:28/28:28 = 2/1 = 2;

114/171 – НОД = 57, значит, 114:57/171:57 = 2/3;

102/153 – НОД = 51, значит, 102:51/153:51 = 2/3.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 74

Источник

Сокращение дробей: правила и примеры

Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Что такое «сокращение дробей»

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

Приведение дробей к несократимому виду

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

6 24 = 6 ÷ 6 24 ÷ 6 = 1 4

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

182 195 = 182 ÷ 13 195 ÷ 13 = 14 15

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Для этого представим исходную дробь в виде:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44

20 44 = 20 ÷ 2 44 ÷ 2 = 10 22

Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:

Источник

Основные сведения о сокращении дробей — правила и свойства сокращения

Что такое «сокращение дробей»

Сокращение дроби — деление ее числителя и знаменателя на какой-то общий делитель.

Условия для общего делителя:

Итогом сокращения является некая новая дробь, которая равна начальной дроби.

Основное свойство дроби

Ключевое свойство дроби: при умножении или делении числителя и знаменателя дроби на одинаковое натуральное число в результате получается дробь, которая равна начальной дроби.

Правило сокращения дробей

Сокращение дробей состоит в том, чтобы в результате получить в числителе и знаменателе минимальные из возможных чисел.

Смысл сокращения заключается в получении несократимой дроби. Для этого требуется разделить числитель и знаменатель на наибольший общий делитель ( Н О Д ). В итоге дробь будет преобразована в несократимую дробь.

a ÷ Н О Д ( a ; b ) b ÷ Н О Д ( a ; b )

Данная дробь является несократимой. Этот вывод сделан на основании свойства Н О Д :

Алгоритм сокращения

Сокращение любой обыкновенной дроби следует выполнять в соответствии со стандартным алгоритмом:

Секретом быстрого сокращения дроби является умение определять Н О Д для числителя и знаменателя. Хорошими помощниками в этом случае станут таблица умножения и навыки разложения чисел на простейшие множители.

При умножении всех общих множителей получается:

Н О Д для 36 и 84 равен 12.

Допускается последовательное сокращение числителя и знаменателя на общий делитель. Данная методика позволяет упростить сокращение дробей, на месте числителя и знаменателя в которых присутствуют крупные числа, а определенный ранее НОД вызывает сомнения.

Характерные примеры

Дана дробь, которую требуется сократить:

Заметим, что в условии задания записана обыкновенная дробь. Воспользуемся стандартным алгоритмом сокращения, то есть выполним деление числителя и знаменателя на общий делитель 3. Получим:

3 15 = 3 ÷ 3 15 ÷ 3 = 1 5

Нужно выполнить сокращение обыкновенной дроби:

Сократить дробь получится, если найти частное от деления числителя и общего делителя, знаменателя и общего делителя. Общим делителем является число 2. Получим:

4 16 = 4 ÷ 2 16 ÷ 2 = 2 8

Далее можно еще раз сократить дробь, то есть разделить числитель и знаменатель на число 2:

Нужно сократить дробь:

В первую очередь следует выполнить разложение чисел, которые записаны в числителе и знаменателе:

Можно исключить общие множители и найти произведение оставшихся:

135 180 = 3 2 × 2 = 3 4

Дана обыкновенная дробь, которую нужно сократить:

18 81 = 18 ÷ 9 81 ÷ 9 = 2 9

Требуется сократить дробь:

150 225 = 50 75 = 10 15 = 2 3

Дана дробь, которую требуется сократить:

Определим Н О Д путем разложения числителя и знаменателя, чтобы получить простые множители:

168 = 2 × 2 × 2 × 3 × 7

240 = 2 × 2 × 2 × 2 × 3 × 5

Найдем произведение всех общих множителей:

Таким образом, Н О Д 168 и 240 составляет 24.

Далее следует разделить числитель и знаменатель дроби на Н О Д :

168 240 = 168 ÷ 24 240 ÷ 24 = 7 10

Нужно выполнить сокращение дроби:

Определим Н О Д путем разложения числителя и знаменателя на простые множители:

360 = 2 × 2 × 2 × 3 × 3 × 5

540 = 2 × 2 × 3 × 3 × 3 × 5

Перемножим все общие множители, получим:

2 × 2 × 3 × 3 × 5 = 180

В результате, Н О Д для 360 и 540 составит 180.

Далее необходимо разделить числитель и знаменатель дроби на Н О Д :

360 540 = 360 ÷ 180 540 ÷ 180 = 2 3

Привести дробь к несократимому виду:

420 = 2 × 2 × 3 × 5 × 7

2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7

Произведение общих множителей равно:

2 × 2 × 3 × 5 × 7 = 420

В результате Н О Д для 420 и 2520 равен 420.

420 2520 = 420 ÷ 420 2520 ÷ 420 = 1 6

Привести дробь к несократимому виду:

1575 = 3 × 3 × 5 × 5 × 7

3450 = 2 × 3 × 5 × 5 × 23

Найдем произведение общих множителей:

Н О Д для 1575 и 3450 составляет 72.

Сократим дробь с помощью деления числителя и знаменателя дроби на НОД:

Источник

Сокращение алгебраических дробей: правило, примеры.

Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.

Смысл сокращения алгебраической дроби

В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.

Сокращение алгебраической дроби представляет собой аналогичное действие.

Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.

Все ли алгебраические дроби подлежат сокращению?

С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.

Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.

Правило сокращения алгебраических дробей

Правило сокращения алгебраических дробей состоит из двух последовательных действий:

Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.

Характерные примеры

Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:

Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).

К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105

Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:

(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105

По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.

Решение

Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:

Однако, более рациональным способом будет запись решения в виде выражения со степенями:

Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).

Решение

Возможно сократить дробь таким образом:

Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

Решение

Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:

Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:

Краткое решение без пояснений запишем как цепочку равенств:

Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.

Решение

На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:

Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:

Теперь становится виден общий множитель, осуществляем сокращение:

Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.

Источник