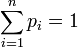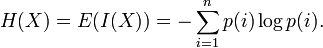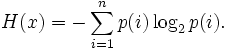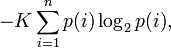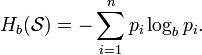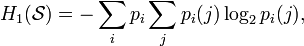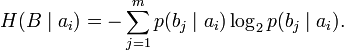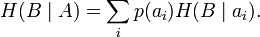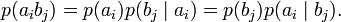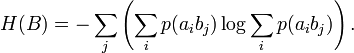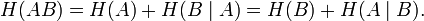что означает термин энтропия с точки зрения теории информации

Энтропия (в теории информации)

В теории информации, энтропия Шеннона, или информационная энтропия — мера неопределённости, связанной со случайной величиной (с.в.); определяет количество информации, содержавшейся в сообщении (обычно в битах или битах на символ); минимальная длина сообщения, необходимая для передачи информации; также абсолютный предел наиболее возможного сжатия без потерь любого сообщения: при представлении сообщения рядом символов, кратчайшее представление, необходимое для передачи сообщения — это энтропия Шеннона в битах на символ, умноженная на число символов в исходном сообщении.

Эквивалентно, энтропия Шеннона — мера среднего информационного содержания с.в., которое наблюдатель (получатель сообщения) теряет, когда ему неизвестно значение (исход) с.в.

Содержание

Определение

Энтропия Шеннона дискретной с.в. , которая может принимать значения , равна величине

Характеризация

Определим и меру информационной энтропии

Информационная энтропия характеризуется следующими пожеланиями (desiderata):

Непрерывность Мера должна быть непрерывной — то есть, изменение значения одной из вероятностей на очень маленькую величину должно изменить энтропию также на маленькую величину. Симметрия Мера не должна меняться, если исходы переупорядочены: и т.д. Максимум Мера должна быть максимальной, если все исходы одинаково вероятны (неопределённость является самой высокой, когда все возможные события равновероятны). Для равновероятных событий энтропия должна увеличиваться с увеличением их числа: Аддитивность Количество энтропии не должно зависеть от того, как система событий разделена на части (подсистемы). Это последнее функциональное отношение характеризует энтропию системы с подсистемами и требует, чтобы энтропия системы могла быть вычислена через энтропии ее подсистем, если мы знаем, как подсистемы взаимодействуют с друг другом. Дан ансамбль из равномерно распределённых элементов, которые произвольно разделены на коробок (подсистем) с элементами соответственно; энтропия всего ансамбля должна быть равна сумме энтропии системы коробок и индивидуальных энтропий коробок, взвешенных с вероятностью обнаружения элемента в соответстувующей коробке. Для положительных целых чисел , Выбор подразумевает, что энтропия конкретного исхода равна нулю:

Можно показать, что любое определение энтропии, удовлетворяющее этим предположениям имеет форму

где — постоянная, соответствующая выбору единицы измерения.

Пояснения

Пример

Дальнейшие свойства

Увеличение энтропии Байеса — закон, согласно которому по мере увеличения выборки сравнения объектов А` для идентификации объекта А, индивидуальные особенности объекта А размываются по отношению к выборке, а идентификация становится бессмысленной. Другими словами с увеличение выборки у объекта А по отношению к ней увеличивается энтропия.

Считается, что закон был открыт эмпирически, до его математического доказательства британским математиком Томасом Байесом. В настоящее время в разных интерпретациях используется в кибернетике, информатике, теории систем, менеджменте и других науках. Некоторые математики и физики считают этот закон еще одним из начал термодинамики.

Пример. Если кто-то захочет установить личность человека, попавшего на видеокамеры, то процесс будет становится тем более бессмысленным, чем с большим количеством людей будет сравнен человек.

Источник

Введение в понятие энтропии и ее многоликость

Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.

В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.

Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона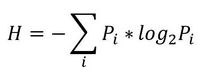
, где Pi это вероятность наступления i-го исхода.

То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событие более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.

Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.

Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).

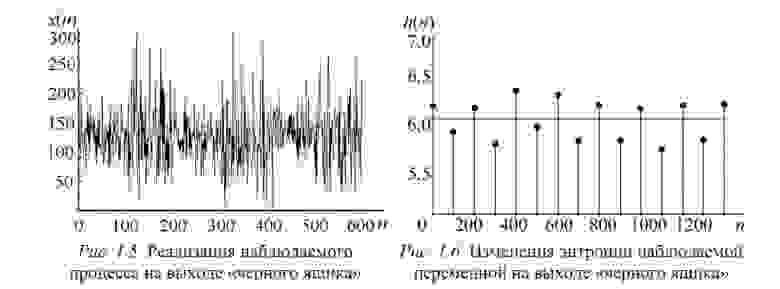
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.

Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).

Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).

Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.

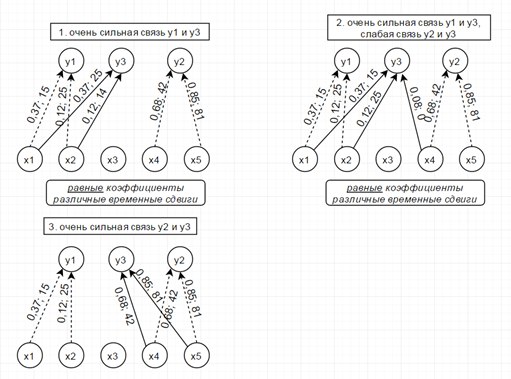
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).

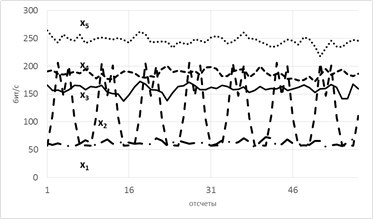
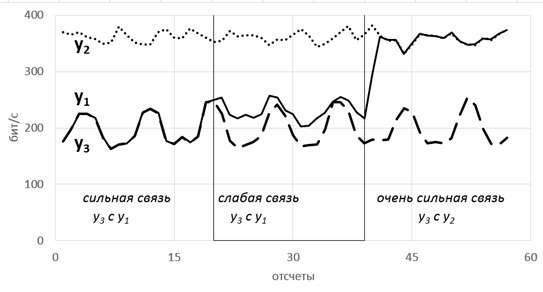
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!

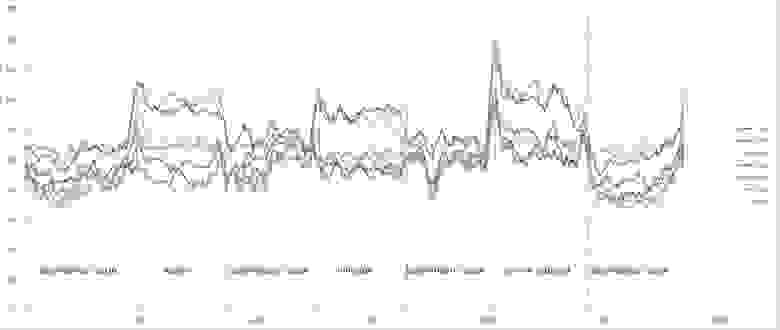
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.

Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).

Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.

Источник

Энтропия (теория информации)

Энтропи́я (информационная) — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.

Для иллюстрации понятия информационной энтропии можно также прибегнуть к примеру из области термодинамической энтропии, получившему название демона Максвелла. Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу.

Содержание

Формальные определения

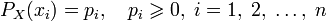
Тогда энтропия будет определяться как:

От основания логарифма зависит единица измерения информации и энтропии: бит, нат или хартли.

Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n ) рассчитывается по формуле:

Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:

где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (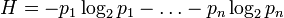), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидание «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д. См.: Цепи Маркова.

Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

Альтернативное определение

Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет условиям:

Свойства

Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию − 2(0,5log₂0,5) = 1 бит на одно кидание (при условии его независимости). У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: 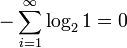. Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.

Математические свойства

Эффективность

Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля — Зива — Велча или арифметического кодирования.

Вариации и обобщения

Условная энтропия

Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть вероятности двухбуквенных сочетаний):

Так, для русского языка без буквы «ё» 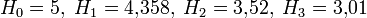. [2]

b1	b2	…	bj	…	bm
a1			…		…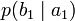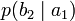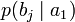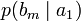
a2			…		…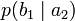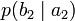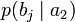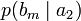
…	…	…	…	…	…	…
ai			…		…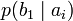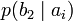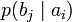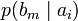
…	…	…	…	…	…	…
am			…		…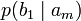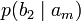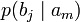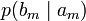

Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:

Взаимная энтропия

Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:

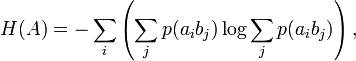
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:

Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем

Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.

История

В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных кодов.

Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.

Источник