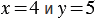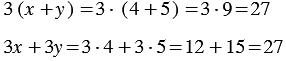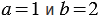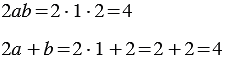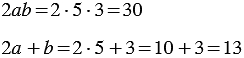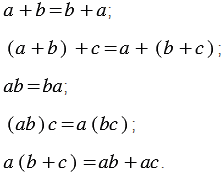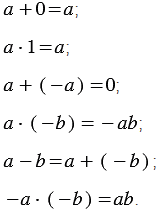что означает тождественно равное выражение
Тождественно равные выражения: определение, примеры.
Получив представление о тождествах, логично перейти к знакомству с тождественно равными выражениями. В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения являются тождественно равными, а какие – нет.
Навигация по странице.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю. Н. Макарычев приведена такая формулировка:
Тождественно равные выражения – это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, которым отвечают одинаковые значения, также называют тождественно равными.
Это определение используется вплоть до 8 класса, оно справедливо для целых выражений, так как они имеют смысл для любых значений входящих в них переменных. А в 8 классе определение тождественно равных выражений уточняется. Поясним, с чем это связано.
Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями. Два числовых выражения, имеющие одинаковые значения, также называются тождественно равными.
В данном определении тождественно равных выражений стоит уточнить смысл фразы «при всех допустимых значениях входящих в них переменных». Она подразумевает все такие значения переменных, при которых одновременно имеют смысл оба тождественно равных выражения. Эту мысль разъясним в следующем пункте, рассмотрев примеры.
Определение тождественно равных выражений в учебнике Мордковича А. Г. дается немного иначе:
Тождественно равные выражения – это выражения, стоящие в левой и правой частях тождества.
По смыслу это и предыдущее определения совпадают.
Примеры тождественно равных выражений
Введенные в предыдущем пункте определения позволяют привести примеры тождественно равных выражений.
Однако области допустимых значений переменных в выражениях могут отличаться. Для примера возьмем выражения x−1 и 

Особую ценность имеет замена одного выражения другим, тождественно равным ему. Такая замена называется тождественным преобразованием выражения, эта тема в силу своей важности заслуживают детального рассмотрения в отдельной статье.
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 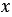
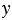

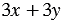
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 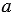
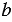
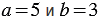
Мы получили разные результаты.
Следовательно, выражения 
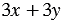
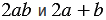
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 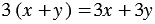
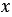
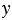
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 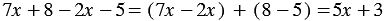
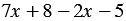
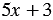
2) 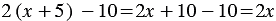
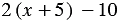
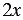
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 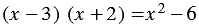
Решение: Приведем контрпример. Если 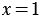
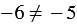
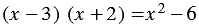
Поделись с друзьями в социальных сетях:
Тождества: определение, обозначение, примеры
Начнем разговор о тождествах, дадим определение понятия, введем обозначения, рассмотрим примеры тождеств.
Что представляет собой тождество
Начнем с определения понятия тождества.
Тождество представляет собой равенство, которое верно при любых значениях переменных. Фактически, тождеством является любое числовое равенство.
По мере разбора темы мы можем уточнять и дополнять данное определение. Например, если вспомнить понятия допустимых значений переменных и ОДЗ, то определение тождества можно дать следующим образом.
Тождество – это верное числовое равенство, а также равенство, которое будет верным при всех допустимых значениях переменных, которые входят в его состав.
Про любые значения переменных при определении тождества речь идет в пособиях и учебниках по математике для 7 класса, так как школьная программа для семиклассников предполагает проведение действий исключительно с целыми выражениями (одно- и многочленами). Они имеют смысл при любых значениях переменных, которые входят в их состав.
Программа 8 класса расширяется за счет рассмотрения выражений, которые имеют смысл только для значений переменных из ОДЗ. В связи с этим и определение тождества меняется. Фактически, тождество становится частным случаем равенства, так как не каждое равенство является тождеством.
Знак тождества
Обычно запись тождества ничем не отличается от записи обыкновенного равенства. Знак тождества может быть применен для того, чтобы подчеркнуть, что перед нами не простое равенство, а тождество.
Примеры тождеств
Обратимся к примерам.
Равенства 2 + 3 = 5 и 7 − 1 = 2 · 3 также можно считать тождествами, так как они являются вернными. Здесь также допустима запись 2 + 3 ≡ 5 и 7 − 1 ≡ 2 · 3 .
Тождества могут содержать не только числа, но также и переменные.
Это значит, что приведенные равенства не являются тождествами.
В математике мы постоянно имеем дело с тождествами. Делая записи действий, производимых с числами, мы работаем с тождествами. Тождествами являются записи свойств степеней, свойств корней и прочие.
Тождество. Тождественные преобразования. Примеры.
Тождества в основном применяются для решения линейных уравнений.
Тождеством называется равенство, которое верно при всех значениях переменных.
Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:
В этих выражениях при всех значениях a и b равенство верное.
2 выражения с равными значениями при всех значениях переменных являются тождественно равными.
Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.
Тождественное равенство обозначают символом «≡» (тройное равенство).
Примеры тождеств.
— Тождество Эйлера (кватернионы);
— Тождество Эйлера (теория чисел);
— Тождество четырёх квадратов;
— Тождество восьми квадратов;
Тождественные преобразования.
Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.
Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.
Выполним тождественные преобразования с такой дробью: 
Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.
Доказательство тождеств.
Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.
Например, доказать тождество:
Вынесем х за скобки:
Это равенство есть тождество, при х≠0 и х≠1.
Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.
5−1 ≠ 5+1 — подставим, к примеру, 5.
Это равенство не тождество.
Разница между тождеством и уравнением.
Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.
Это выражение верно лишь при х = 10.
Тождеством будет равенство, которое не содержит переменных.
Тождественные преобразования
Что такое тождественные преобразования
Тождество — это равенство, выполняемое на всем множестве значений переменных, которые в него включены.
К примеру, тождествами являются, в том числе, квадратные выражения:
a 2 − b 2 = ( a + b ) ( a − b )
( a + b ) 2 = a 2 + 2 a b + b 2
В рассмотренных выражениях любые значения a и b обращают их в верные равенства, что полезно знать при решении примеров.
Тождественно равными выражениями называют такие два выражения, которые обладают равными значениями при всех значениях переменных.
Данное равенство существует только в том случае, когда:
Разница между тождеством и уравнением заключается в том, что тождество является верным при любом из значений переменных. Уравнение же верно лишь в том случае, когда имеется одно или несколько значений переменных.
В этом случае тождество не включает в себя переменные.
Замена чисел и выражений тождественно равными им выражениями
Тождественное преобразование выражения (преобразование выражения) представляет собой замену одних выражений на другие, которые тождественно равны между собой.
Данное объяснение преобразований позволяет значительно упростить решение задач. К примеру, для этого используют законы сокращенного умножения, арифметические свойства и другие тождества.
Рассмотрим конкретный пример:
Выполним работу по тождественным преобразованиям этой дроби:
x 3 – x x 2 – x = x ( x 2 – 1 ) x – 1 = x ( x – 1 ) ( x + 1 ) x ( x – 1 ) = x + 1
x 3 – x x 2 – x = x + 1
Доказательство тождеств
В процессе доказательства тождества необходимо выполнить ряд действий:
В качестве самостоятельного примера для тренировки докажем следующее тождество:
x 3 – x x 2 – x = x 2 + x x
x ( x 2 – 1 ) x ( x – 1 ) = x ( x + 1 ) x
Заметим, что можно сократить х :
( x – 1 ) ( x + 1 ) x – 1 = x + 1
Заключим, что рассмотренное равенство является тождеством, если х ≠ 0 и х ≠ 1
Когда требуется доказать, что равенство не относится к тождеству, следует определить одно допустимое значение переменной, при котором полученные числовые выражения обращаются в неравные друг другу. К примеру:
x 2 – x x = x 2 + x x → x ≠ 0
Упростим вычисления с помощью сокращения х :
Данное равенство не является тождеством.
Примеры тождеств
Изучить тождества на практике можно с помощью решения задач на различные тождественные преобразования алгебраических выражений. Ключевой целью таких действий является замена начального выражения на выражение, которое ему тождественно равно.
От перестановки местами слагаемых сумма не меняется:
От перестановки местами сомножителей произведение не меняется:
Согласно данным правилам, можно записать примеры тождественных выражений:
При наличии в сумме более двух слагаемых допускается группировать их путем заключения в скобки. Также можно предварительно переставлять эти слагаемые местами:
a + b + c + d = ( a + c ) + ( b + d )
Аналогичным способом группируют сомножители в произведении:
a × b × c × d = ( a × d ) × ( b × c )
Приведем примеры таких тождественных преобразований:
15 + 6 + 5 + 4 = ( 15 + 5 ) + ( 6 + 4 )
6 × 8 × 11 × 4 = ( 6 × 4 × 8 ) × 11
При увеличении или уменьшении обеих частей тождества на одинаковое число, данное тождество остается верным:
( a + b ) ± e = ( c + d ) ± e
Равенство сохраняется также при умножении или делении обеих частей этого равенства на одно и то же число:
( a + b ) × e = ( c + d ) × e
( a + b ) ÷ e = ( c + d ) ÷ e
Запишем несколько примеров:
35 + 10 = 9 + 16 + 20 ⇒ ( 35 + 10 ) + 4 = ( 9 + 16 + 20 ) + 4
42 + 14 = 7 × 8 ⇒ ( 42 + 14 ) × 12 = ( 7 × 8 ) × 12
Какую-либо разность допускается записывать, как сумму слагаемых:
Аналогичным способом можно выполнить замену частного на произведение:
Рассмотрим примеры тождественных преобразований:
Заменить математическое выражение на более простое можно с помощью арифметических действий:
Преобразования следует выполнять с соблюдением алгоритма:
14 + 6 × ( 35 – 16 × 2 ) + 11 × 3 = 14 + 18 + 33 = 65
20 ÷ 4 + 2 × ( 25 × 3 – 15 ) – 9 + 2 × 8 = 5 + 120 – 9 + 16 = 132
В арифметических выражениях можно избавляться от скобок при необходимости. Исходя из знаков в выражении, определяются правила, согласно которым раскрывают скобки.
Рассмотрим несколько примеров преобразований с помощью раскрытия скобок:
117 + ( 90 – 74 – 38 ) = 117 + 90 – 74 – 38
22 × ( 8 + 14 ) = 22 × 8 + 22 × 14
18 ÷ ( 4 – 6 ) = 18 ÷ 4 – 18 ÷ 6
Другим распространенным действием при упрощении выражений, содержащих скобки, является вынесение за них общего множителя. В результате в скобках остаются слагаемые, поделенные на вынесенный множитель. Данный способ преобразования можно применять в выражениях, которые содержат буквенные переменные.
3 × 5 + 5 × 6 = 5 × ( 3 + 6 )
28 + 56 – 77 = 7 × ( 4 + 8 – 11 )
31 x + 50 x = x × ( 31 + 50 )
В процессе тождественных преобразований часто применяют формулы для сокращенного выражения.
Примеры тождественных преобразований:
( 31 + 4 ) 2 = 31 2 + 2 ⋅ 31 ⋅ 4 + 4 2 = 1225