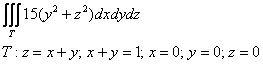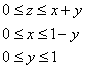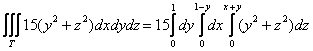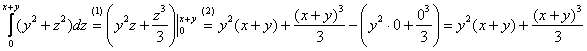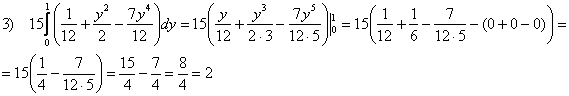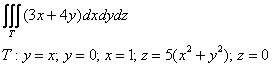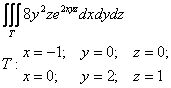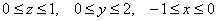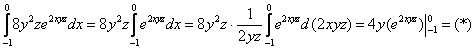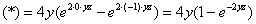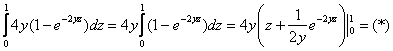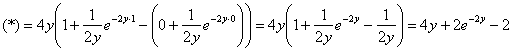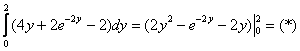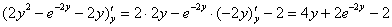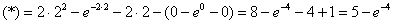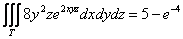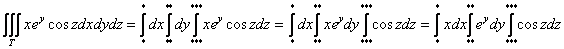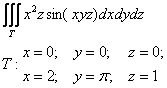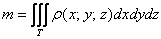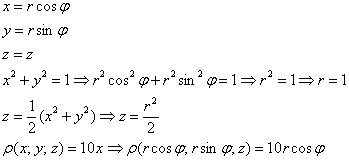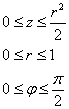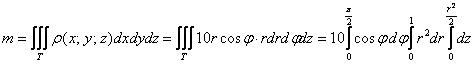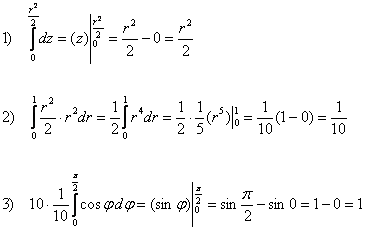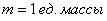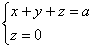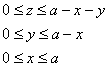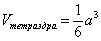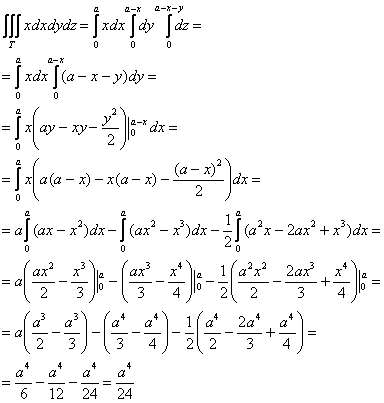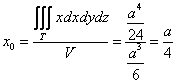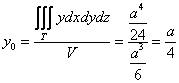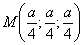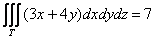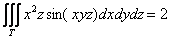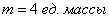что означает тройной интеграл

18.10.202329.06.2023 admin 0 Comments

Что означает тройной интеграл

Если такой предел существует, то функция f ( M ) называется интегрируемой в области V ; всякая непрерывная в ограниченной замкнутой области V функция f ( M ) интегрируема в ней. В дальнейшем мы будем рассматривать только непрерывные функции.

Координаты центра тяжести тела вычисляются по формулам:

1. Вычисление тройного интеграла в декартовой системе координат

Наиболее простой вид формула (6.12) принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями :

Чтобы вычислить полученный интеграл, положим 1– x = t ; тогда dx = – dt ; при этом t = 1 при x = 0 и t = 0 при x = 1.

2. Вычисление тройного интеграла в цилиндрических координатах

В этом случае тройной интеграл вычисляется по формуле

С учетом формулы замены (6.15) можем вычислить заданный тройной интеграл:

Обратим внимание на то, что, не переходя к цилиндрическим координатам, мы получили бы достаточно сложное трехкратное интегрирование согласно формуле (6.12)

Примечание. Переход к цилиндрическим координатам рационален, когда область интегрирования образована цилиндрической или конической поверхностью

3. Вычисление тройного интеграла в сферических координатах

Если область интегрирования V представляет собой шар или его часть (граница шара x 2 + y 2 + z 2 = R 2 в сферических координатах имеет очень простой вид ρ = R ), то удобно переходить к сферическим координатам.

В этом случае тройной интеграл вычисляется по формуле

Источник

Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла

Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов 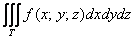, у которых подынтегральная функция трёх переменных в общем случае отлична от константы и непрерывна в области ; а также познакомимся с физическими приложениями тройного интеграла

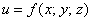
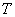
Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла. Остальным же предлагаю немного повторить производные функции трёх переменных, поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции .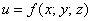

Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:

Вычислить тройной интеграл

На практике тело также обозначают буквой 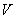, но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.

Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойствами линейности и представлять интеграл в виде 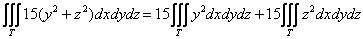. Хотя если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.

В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость 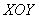представляет собой до боли знакомый треугольник:

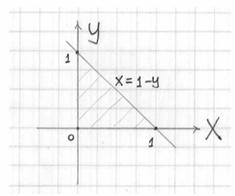
Сверху тело ограничено плоскостью 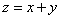, которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью , т.е. решаем простейшую систему: – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость действительно представляет собой треугольник.

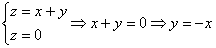
Не сложен здесь и пространственный чертёж: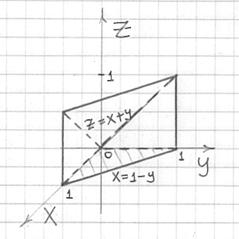

В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.

Выберем следующий порядок обхода тела:

И перейдём к повторным интегралам:

Актуализируем следующее элементарное правило:

Когда функция 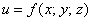интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.

Разбираемся с интегралами:

(1) При интегрировании по «зет» 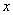и считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
, что и требовалось проверить.

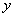
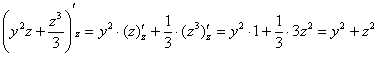
(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования 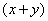, затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!

Сносим трофей в следующий интеграл. По существу, решение свелось к двум переменным и к двойному интегралу:

(1) Используем свойства линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Следует отметить, что не возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рациональный способ (можете попробовать).

(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжело, мысленно замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».

(3) Интегрируем по «икс» и выполняем проверку: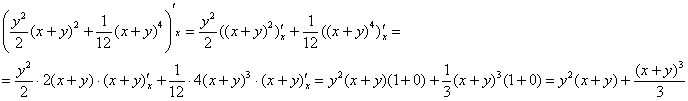

(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось интегрирование) подставляем 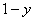, затем – ноль. После подстановок буквы «икс» остаться не должно!

Причёсываем результат и сносим его в последний интеграл, не теряя находящуюся там константу:

Ответ:

Результат безразмерен – просто число и всё.

Следующий пример для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец оформления задачи в конце урока.

До сих пор мы рассматривали два способа решения – это проецирование на плоскость 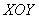и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.

Наверняка многие обратили внимание, что в Примере № 13 я выбрал более редкий порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность.
В результате нахождения интеграла 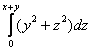получена сумма , в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой одинаково легко выразить ) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:

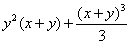
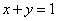
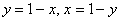
Вычислить тройной интеграл

Решение: область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед: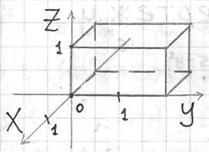

У незамысловатых областей можно не обращать внимания на проекцию и придерживаться следующего правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь очевидны

Но вот с порядком обхода не всё так просто. Если выбрать традиционный путь и сначала интегрировать по «зет», то получается неприятный интеграл 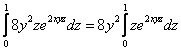, который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»: , тут даже дважды по частям.

Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные 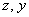, а значит, и множитель считаются константами:

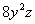
Перед тем, как подставить пределы интегрирования, не помешает проверка:
– получена исходная подынтегральная функция.

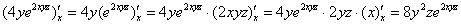
Буква «икс» испарилась, как оно и должно быть.

Осталось 2 направления обхода 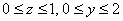, и следующий интеграл рациональнее взять по «зет» чтобы множитель считался константой:

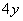
Промежуточная проверка: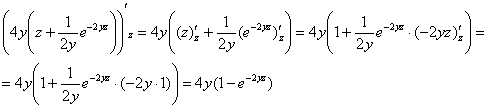

Гуд.

В качестве дополнительного контроля снова смотрим, исчезла ли после подстановки переменная, по которой интегрировали («зет»).

И, наконец, оставшееся направление обхода 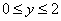и оставшийся интеграл:

Проверка:

При подстановках следует проявлять повышенное внимание, так, например, при подстановке нуля в выражение 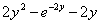второе слагаемое можно машинально счесть за ноль.

На чистовике, конечно же, не нужно всё расписывать так подробно, анализ порядка интегрирования и промежуточные проверки осуществляются мысленно либо на черновике. Решение оформляется стандартно в 3 пункта, но читатели с хорошим уровнем подготовки могут записать его и «одной строкой»:

Ответ:

Наверное, это понятно, но на всякий случай закомментирую: буквенные множители-константы следует перемещать справа налево последовательно и без «перескоков» – до тех пор, пока каждая буква «не встретит свой интеграл». Условный пример:

Аналогичное задание для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец чистового оформления задачи в конце урока.

Чем дальше, тем интереснее:

Физические приложения тройного интеграла

Но сначала разомнёмся физически, тело – в дело =) Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок. Можно коробку. Теперь походим по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором. …Очень хорошо, молодцы. В результате ваших трудов получено ограниченное тело неоднородной плотности. Как говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что физическая плотность – есть отношение массы к объёму, например, 100 грамм на кубический метр.

Ставим мешок рядышком и читаем дальше. Рассмотрим неоднородное (переменной плотности) тело 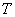. Если известна непрерывная в области функция плотности тела, то его масса равна следующему тройному интегралу:

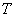
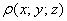
Возможно, не всем понятен смысл функции плотности. Поясняю: если взять произвольную точку 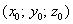, принадлежащую телу , то значение функции будет равно плотности тела в данной точке.

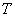
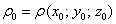
Только не стОит находить функцию 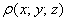для пакета с мусором, иначе шнобелевская премия обеспечена =) …Хотя, с другой стороны нашлись же энтузиасты оценить суммарную площадь поверхности индийских слонов и создать математическую модель пивной пены.

Однако разрядились, и хватит. Разберём несколько тематических задач:

Вычислить массу неоднородного тела, ограниченного поверхностями 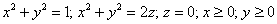, если известна функция его плотности .

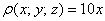
Решение: искомое тело ограничено цилиндром 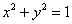сбоку, эллиптическим параболоидом – сверху и плоскостью – снизу. Дополнительные условия «загоняют нас» в 1-й октант, и проекция тела на плоскость представляет собой соответствующую «четвертинку» единичного круга:

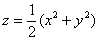
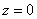
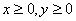
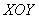
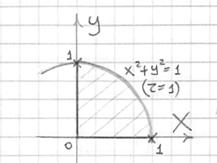
Аналитическим методом уточним высоту, на которой параболоид пересекает цилиндр:
и выполним пространственный чертёж:

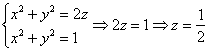
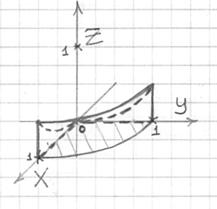
Проекция сразу же наводит на мысль о переходе к цилиндрической системе координат:

Порядок обхода тела очевиден:

Таким образом:

Вычисления элементарны:

Ответ:

Следующий пример для самостоятельного решения:

Вычислить массу неоднородного тела, ограниченного поверхностями 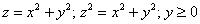, если известна функция его плотности .

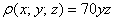
Краткое решение в конце урока

И старая песня о главном:

Центр тяжести тела

Подобно тому, как задача о вычислении центра тяжести плоской фигуры вычислялась с помощью двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным способом с помощью тройного интеграла.

Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести, то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени не реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.

Центр тяжести 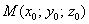неоднородного тела рассчитывается по формулам:

, где – функция плотности тела, а – масса тела.

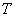
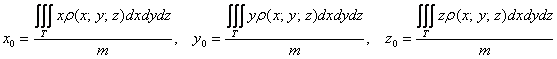
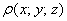
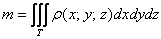
Если тело однородно (золотое, серебряное, платиновое и т.д.), то формулы упрощаются. Так как плотность 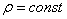постоянна, и масса – есть произведение плотности на объём, получаем:
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла .

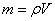
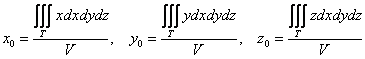
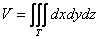
Для центра тяжести однородного тела справедливы следующие утверждения:

– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);

– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;

– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.

Как видите, практически полная аналогия с центром тяжести плоской фигуры.

Ну и, само собой, не могу не порадовать вас заключительной задачей:

Найти центр тяжести однородного тела, ограниченного поверхностями 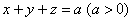, . Выполнить чертежи данного тела и его проекции на плоскость .

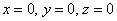
Решение: искомое тело ограничено координатными плоскостями и плоскостью 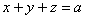, которую в целях последующего построения удобно представить в отрезках: . Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:

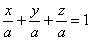
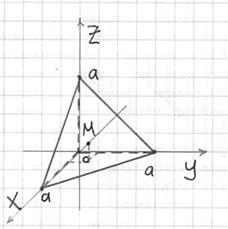
На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.

Проекция тела на плоскость 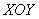очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему:

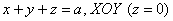
Подставляем значение 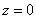в 1-е уравнение: и получаем уравнение «плоской» прямой:

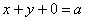
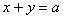
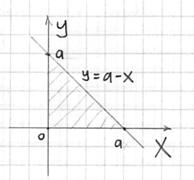
Координаты 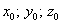центра тяжести тела вычислим по формулам
, где – объём тела.

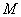
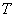
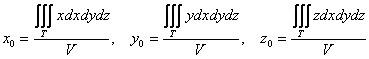
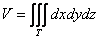
Выберем «классический» порядок обхода:

1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем случае параллелепипед представляет собой куб с ребром «а», и соответственно:

Осталось аккуратно провести чистовые вычисления (желающие могут потренироваться и выполнить их самостоятельно). В примерах с громоздкими преобразованиями рекомендую записывать решение столбиком – меньше шансов запутаться:

2) Вычислим «иксовый» интеграл:

Таким образом, «иксовая» координата центра тяжести:

Ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь тела».

Ввиду симметрии тетраэдра две другие координаты должны получиться такими же. Теперь ошибочный ответ практически исключён!

3) Следующая «простыня»:

В результате:

4) И заключительный, более короткий интеграл:

Отмечаем на чертеже найденную точку центра тяжести и её же записываем в
ответ:

Осталось взять мешок с мусором и чувством глубокого морального удовлетворения выбросить его… нет, в окно не надо =)

Что осталось за кадром? В сетку урока не попала редко встречающая на практике сферическая система координат, в которой положение любой точки пространства однозначно определяется одним расстоянием и двумя углами. И до сферических координат у меня таки дошли пальцы в статье Дивергенция векторного поля.

Вы постоянно сетовали на простоту примеров, и поэтому я просто не мог вам не рассказать о криволинейных и поверхностных интегралах, а также основах векторного анализа.

Пример 14: Решение: изобразим проекцию данного тела на плоскость :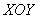

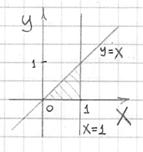
Сверху тело ограничено эллиптическим параболоидом .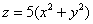
Выберем следующий порядок обхода: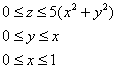

Таким образом: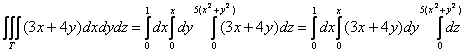

Примечание: в «зетовом» интеграле сумма 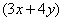считается константой, поэтому её удобно сразу вынести в следующий интеграл.

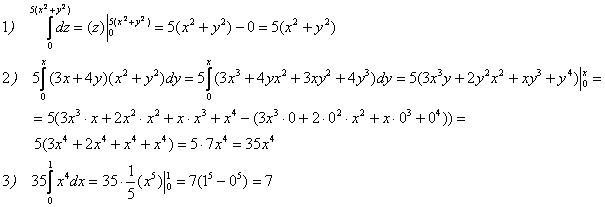
Ответ:

Пример 16: Решение: выполним чертёж: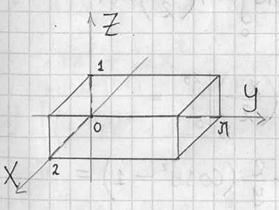

Выберем следующий порядок обхода тела: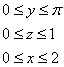

Таким образом: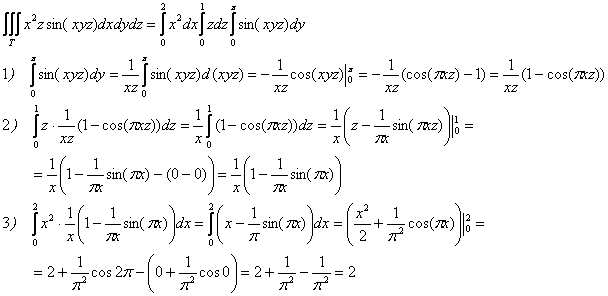

Ответ:

Пример 18: Решение: искомое тело ограничено эллиптическим параболоидом 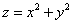снизу и конической поверхностью – сверху; параболоид и конус пересекаются в плоскости по окружности (выкладки и чертёж – см. в Примере № 9 страницы Тройные интегралы). Поскольку , то речь идёт о правом (относительно плоскости ) полупространстве, и проекцией тела на плоскость является верхний полукруг единичного радиуса:

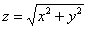
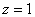
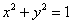
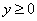
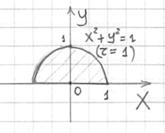
Массу тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат: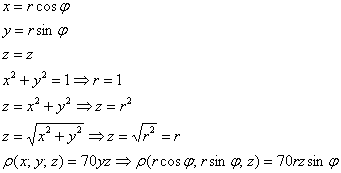

Порядок обхода тела: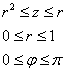

Таким образом:

Ответ: