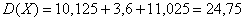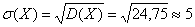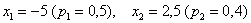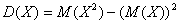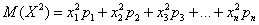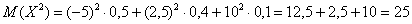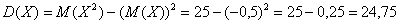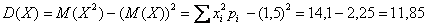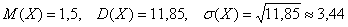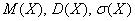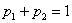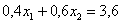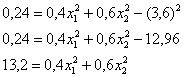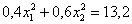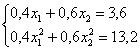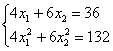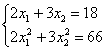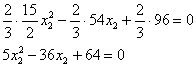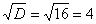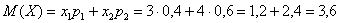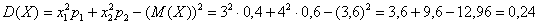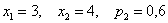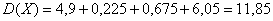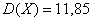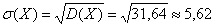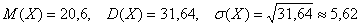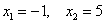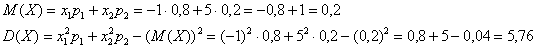дисперсия что это в математике
Дисперсия дискретной случайной величины.
Среднее квадратическое отклонение
Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:
«Снайперское» математическое ожидание равно 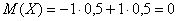
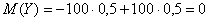
Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.
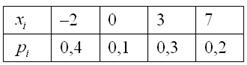
Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:
Там мы нашли неутешительное математическое ожидание 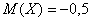
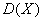
Выясним, насколько далеко «разбросаны» выигрыши/проигрыши относительно среднего значения. Очевидно, что для этого нужно вычислить разности между значениями случайной величины и её математическим ожиданием:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
Теперь вроде бы нужно просуммировать результаты, но этот путь не годится – по той причине, что колебания влево будут взаимоуничтожаться с колебаниями вправо. Так, например, у стрелка-«любителя» (пример выше) разности составят 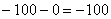
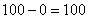
Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей: 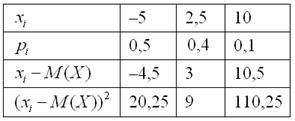
И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:
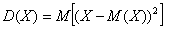
Вспоминаем, как находить матожидание. Перемножаем квадраты разностей на соответствующие вероятности (продолжение таблицы):
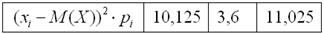
и суммируем результаты:
Не кажется ли вам, что на фоне выигрышей 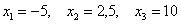
Иногда это значение называют стандартным отклонением.
В чём его смысл? Если мы отклонимся от математического ожидания 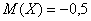
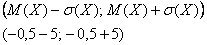
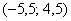
Однако так сложилось, что при анализе рассеяния почти всегда оперируют понятием дисперсии. Давайте разберёмся, что она означает применительно к играм. Если в случае со стрелками речь идёт о «кучности» попаданий относительно центра мишени, то здесь дисперсия характеризует две вещи:
Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим 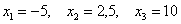
Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:
Игра с низкой дисперсией – это осторожная игра. Игрок склонен выбирать самые надёжные схемы, и в ситуации неопределённости не ставит слишком большие деньги. Например, система «красное/чёрное» в рулетке (см. Пример 4 статьи Случайные величины).
Игра с высокой дисперсией. Её часто называют дисперсионной игрой. Это авантюрный или агрессивный стиль игры, где игрок выбирает «адреналиновые» схемы. Вспомним хотя бы «Мартингейл», в котором на кону оказываются суммы, на порядки превосходящие «тихую» игру предыдущего пункта.
То же самое происходит на Форексе, других биржах и так далее – примеров масса.
Причём, во всех случаях не важно – на копейки ли идёт игра или на тысячи долларов. На любом уровне есть свои низко- и высокодисперсионные игроки. Ну а за средний выигрыш, как мы помним, «отвечает» математическое ожидание.
Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:
Формула для нахождения дисперсии
Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой: 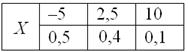
и найденное матожидание 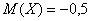
Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание 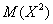
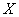
В данном случае:
Таким образом, по формуле:
Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).
Осваиваем технику решения и оформления:
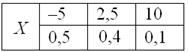
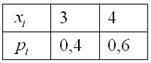
Дискретная случайная величина задана своим законом распределения:
Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в дурдоме с определёнными вероятностями 🙂
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения 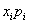
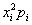
Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: 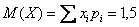
Дисперсию вычислим по формуле:
И, наконец, среднее квадратическое отклонение:
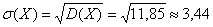
Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:
вот здесь уже трудно ошибиться 🙂
Ответ:
Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!
Пара заданий для самостоятельного решения:
Вычислить дисперсию случайной величины 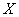
И аналогичный пример:
Дискретная случайная величина задана своим законом распределения:
Найти
Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.
Решения и ответы внизу страницы.
В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:
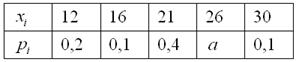
Дискретная случайная величина 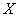
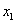
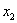
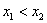
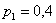
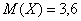
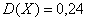
Найти 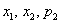
Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:
и поскольку 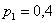
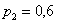
Осталось найти 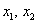
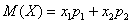
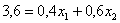
ОК, едем дальше. По формуле вычисления дисперсии:
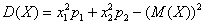
или:
О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:
Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:
и делим на 2:
Вот так-то лучше. Из 1-го уравнения выражаем:
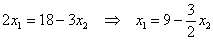
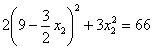
Возводим в квадрат и проводим упрощения: 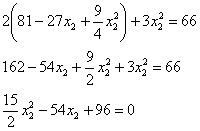
Умножаем на 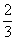
В результате получено квадратное уравнение, находим его дискриминант:
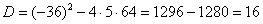
и у нас получается два решения:
1) если 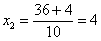
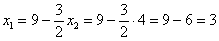
2) если 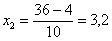
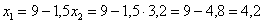
Условию 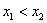
и выполним проверку, а именно, найдём матожидание:
и дисперсию:
В результате получены исходные значения, что и требовалось проверить.
Ответ:
Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:
Случайная величина 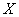
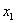
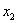
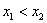
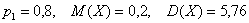
Тут вычисления попроще.
Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!
Пример 7. Решение: вычислим математическое ожидание: 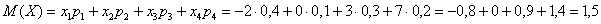
Вычислим дисперсию по определению: 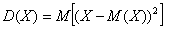
Заполним расчётную таблицу: 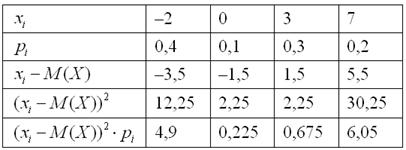
Таким образом:
Ответ:
Пример 8. Решение: случайная величина может принять только 5 значений, поэтому: 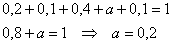
Заполним расчётную таблицу: 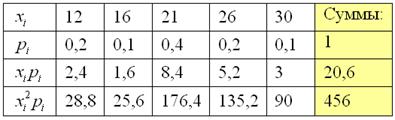
Математическое ожидание: 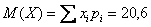
Дисперсию вычислим по формуле: 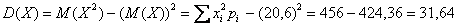
Среднее квадратическое отклонение:
Ответ:
Пример 10. Решение: т.к. случайная величина 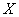
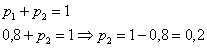
По определению математического ожидания: 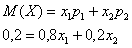
По формуле вычисления дисперсии: 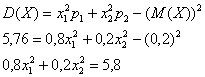
Составим и решим систему: 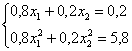
Умножим оба уравнения на 5: 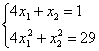
Из первого уравнения выразим: 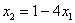
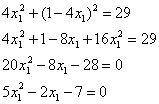
Решим полученное квадратное уравнение: 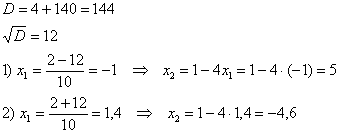
Условию 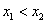
Ответ:
Проверка:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5