для чего используется метод координат
Творческие проекты и работы учащихся
В процессе работы над индивидуальным проектом по математике «Координаты в нашей жизни» учеником 6 класса школы была поставлена и реализована цель, выяснить, где еще кроме математики применяется система координат. Для этого автор дает определение понятиям «координаты» и «система «координат», кратко излагает историю возникновения системы координат.
Подробнее о проекте:
В готовом творческом и исследовательском проекте по математике «Координаты в нашей жизни» автор выполняет практические задания, рассчитанные на построение изображений на координатной плоскости, а также изучает технологию расчета координатных данных для выполнения «рисунка» в прямоугольной системе координат. Предложенный детский проект позволяет научиться свободно ориентироваться на координатной плоскости и на географической карте.
Оглавление
Введение
1. Координаты. Системы координат.
1.1. История возникновения системы координат.
1.2. Координатная плоскость в математике.
1.3. Координаты вокруг нас.
1.4. Географические координаты.
2. Изображения на координатной плоскости.
2.1. Построение изображений на координатной плоскости.
2.2. Создание «рисунков» в прямоугольной системе координат.
Заключение
Приложение
Введение
Подробное изучение координатной плоскости необходимо. Ведь координаты- это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять средства алгебры и математического анализа при решении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию.
В окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта.
Например, координаты Кемерово: 37,60 восточной долготы и 55,80 северной широты. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
Проблема: С координатами в геометрии мы сталкиваемся постоянно, а где еще применяется метод координат?
Цель: выяснить, где еще кроме математики применяется система координат.
История возникновения системы координат
Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту (см.приложение 1,рис.1).
До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты.
Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.
Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Координатная плоскость в математике
Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
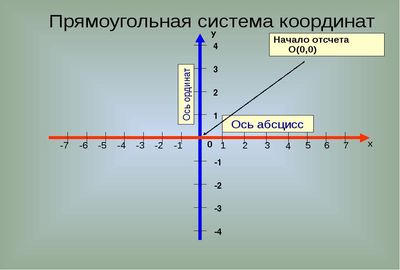
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх». На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают Х и называют осью абсцисс, вертикальную прямую обозначают У и называют осью ординат.
Две перпендикулярные оси Х и У с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал (см.приложение 1,рис. 2).
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки, пересечение другой прямой с осью ординат – это координата точки. Сначала указывают координату, потом. Точка имеет координаты. Аналогично находим координаты точки, она имеет координаты.
Координаты вокруг нас
Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда. 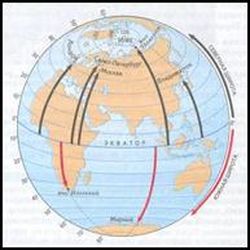
Координаты окружают нас повсюду:
Географические координаты
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария.
Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку.
Построение изображений на координатной плоскости
У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо».
Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.
Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.
Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..
Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.
Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в «ручке» которого – Полярная.
Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.
Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит.
Создание «рисунков» в прямоугольной системе координат
На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.
Заключение
В результате проведения исследования я доказал, что координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека.
В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.
Приложение
Карточка № 1. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
Карточка № 2. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
Карточка № 3. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
Карточка № 4. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
Ответы: 1 – утенок; 2 – заяц; 3 – белка; 4 – кошка.
Координаты на прямой
Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.
Особенностью способа является нахождение геометрических тел уравнениями. Такой подход позволяет исследовать фигуры и решать задания, взяв за основу алгебраические формулы.
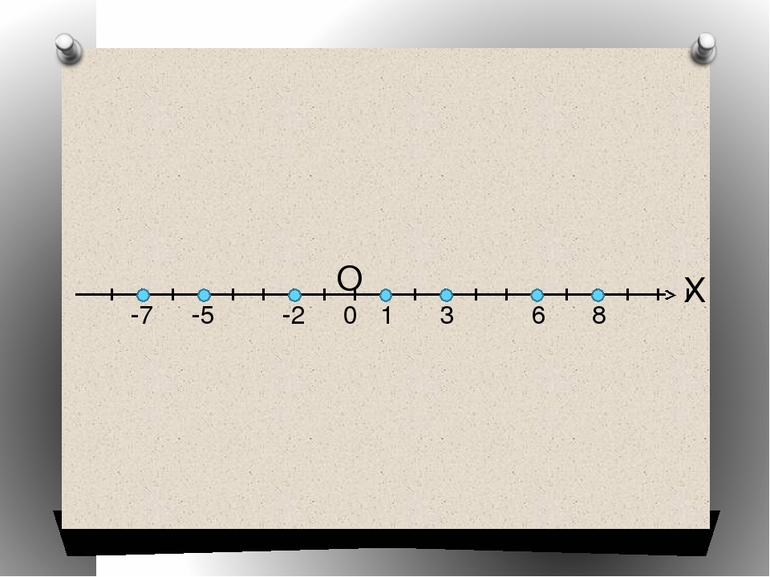
Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.
Принимать она может три значения:
При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.
Расположение на плоскости
Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.
Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.
Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.
Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.
В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.
Скалярное произведение
Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.
Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB 2 = OA 2 + OB 2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.
В итоге получится: |a-b| 2 = |a| 2 + |b| 2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a| 2 + |b| 2 — |a — b| 2 ) /2. Подставив координаты в формулу, получим следующее: a*b = (x1 2 + y1 2 + x2 2 + y2 2 — (x1-x2) 2 + (y1-y2) 2 ) /2 = x1*x2 + y1*y2. Равенство доказано.
Основные формулы
Кроме нахождения длины отрезка, к основным формулам относят:
Для понимания формул нужно знать о векторном и смешанном произведении векторов, а также об определителе матрицы. Зная их, можно решать задачи по вычислению элементов простейших многогранников, находить площади и объёмы.
Нахождение угла
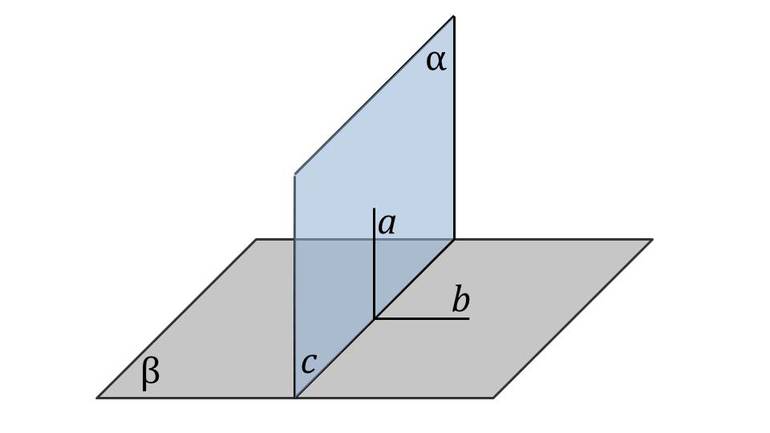
Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:
Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.
Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:
Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2 ½ * ¾ ½ ) = 1 / (6 ½ /2) = 2/6 ½ = 6 ½ / 3. Соответственно, угол равен: α = arccos = 6 ½ / 3.
Вычисление площади и высоты
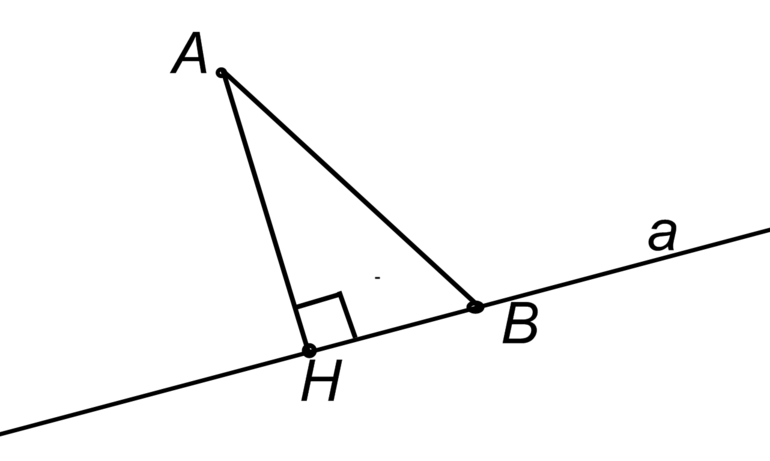
Таким образом, у треугольника две стороны равны, а значит, он равнобедренный. У найденных сторон общей точкой является B (вершина). Следовательно, углы A и C будут равны. Что и требовалось доказать.
Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.
В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).
Высота находится как корень квадратный из двух точек: BH = ((-3−1) 2 + (4−1) 2 ) ½ = (16+9) ½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4) 2 + (-3−5) 2 ) ½ = (36 + 64) ½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.
Расчёт на онлайн-калькуляторе
Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.
Пользователю необходимо ввести условие задания, при этом система будет сама направлять действия и в случае каких-либо ошибок укажет на них, а затем нажать кнопку «Рассчитать». Привлекательность таких сайтов состоит ещё и в том, что ответ будет содержать объяснения с необходимыми формулами и рисунками.
Проект «Метод координат в математике и географии»
Описание презентации по отдельным слайдам:
Учебный комплекс авторской физико-математической школы-лицея № 61. ПРОЕКТ «Метод координат в математике и географии» Выполнили: учащиеся 7 Б и 7 В классов УК АФМШЛ № 61 Евлашков Даниил Литтау Роман Хегай Владимир Руководитель: Горборукова Н.В. г. Бишкек – 2012 г.
Определение местоположения того или иного предмета на поверхности Земли или какой-либо точки на плоскости – это определение их адреса. «Адрес» в географии – географическая широта; географическая долгота; абсолютная высота. «Адрес» в математике – абсцисса, ордината точки на координатной плоскости
Цель проекта: Исследовать и сравнить способы определения «адреса» объекта в географии и математики.
Задачи проекта: Ответить на следующие вопросы: Кто, когда и для чего впервые ввел понятие «координаты»? Существует ли генетическая связь между понятиями «географические координаты» и «координатный метод» в математике? Или это слова-омонимы? На развитие каких наук оказал влияние метод координат? Какие еще виды систем координат помимо прямоугольной существуют и используются человеком в настоящее время в практической деятельности?
Историческая справка. Во II – III веках до н. э. меридианы и параллели впервые появились на карте Эратосфена. Однако, они еще не представляли собой координатной сетки.
Во II в. до н. э. Гиппарх впервые разделил круг на 360 частей и предложил опоясать на карте Земной шар меридианами и параллелями. Ввел понятие – экватор, провел параллели и через полюса провел меридианы. Таким образом, была создана картографическая сеть и стало возможным наносить на карту географические объекты.
Завершил плеяду великих античных астрономов и географов Клавдий Птолемей (190 – 168 г.г. до н. э.). В своем труде «Руководство по географии» в 8 книгах дал описание свыше 8000 географических объектов с указанием их географических координат: широты и долготы.
Почему географические широта и долгота измеряются в градусах? Географическая широта – это величина дуги меридиана от экватора до заданной точки. Из курса геометрии известно, что дуги измеряются как в линейных величинах, так и в угловых: градусах и радианах. Географическая долгота – это величина дуги параллели от нулевого меридиана до заданной точки. Видно, что географические координаты – понятие математическое.
Рене Декарт (1596-1650) – французский математик, философ, физик и физиолог. Декарт является одним из создателей аналитической геометрии, современной алгебраической символики, а метод задания кривой с помощью уравнения был решающим шагом к понятию функции. В математике именно ему принадлежит основная заслуга в создании метода координат, который был положен в основу аналитической геометрии.
Сравним системы координат в математике и географии. 1. Для определения положения объекта на поверхности Земли необходимы 2 координаты: долгота и широта. 2. Для определения положения точки на плоскости необходимы 2 координаты: абсцисса и ордината. 3. Параллели и меридианы взаимно перпендикулярны. 4. Оси OX и OY взаимно перпендикулярны. 5. Для определения точки в пространстве требуется 3 – я координата: абсолютная высота (в географии); аппликата в математике. 6. Экватор и нулевой меридиан делят поверхность земного шара на 4 части 7. Координатные оси делят плоскость на 4 части, а пространство на 8 частей.
Полярные и сферические координаты. Полярная система координат включает в себя т.О – полюс и луч – полярную ось. Каждой точке на плоскости соответствует пара чисел Р(r; ф), угол между направлением на объект и полярной осью и расстояние до объекта В географии аналогом полярных координат является азимут. Для определения местоположения объекта требуется знать угол между направлением на предмет и направлением на север и расстояние до объекта.
Сферической системой координат пользуются, если необходимо определить положение точки в пространстве. Этот метод используется в аэронавигации. С помощью радара определяют 3 координаты: кратчайшее расстояние по прямой до самолета; угол, под которым самолет виден над горизонтом; угол между направлением на самолет и направлением на север
Диаграмма Эйлера – Венна (для прямоугольных систем координат)
Диаграмма Эйлера – Венна (для полярных систем координат).
Выводы: 1. Слова «геометрия» и «география» имеют древнегреческое происхождение и связаны с практической деятельностью людей на поверхности Земли. 2. Географические широта и долгота измеряются в градусах, так как представляют собой дуги окружностей, стягивающих центральные углы, т. е. являются математическими величинами. 3. И в математике, и в географии используются как прямоугольные, так и полярные координаты. 4. В прямоугольных системах координат оси (экватор и нулевой меридиан, оси OX и OY) взаимно перпендикулярны и делят плоскость на 4 части: Северное, Южное, Западное и Восточное полушария в географии и I, II, III, IV квадранты. 5. Положение точки на плоскости задается 2 координатами: широтой и долготой в географии, абсциссой и ординатой в математике. 6. При определении положения объекта в пространстве появляется третья координата: абсолютная высота в географии и аппликата в математике. 7.Для задания полярных координат необходимы: точка отсчета, угол поворота, расстояние от полюса до заданной точки.
СПАСИБО ЗА ВНИМАНИЕ!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Проект «Метод координат в математике и географии».
Проект выполнен под руководством учителя УК АФМШЛ № 61 г Бишкек Горборуковой Н.В.
1. Название проекта: «Метод координат в математике и географии».
2. Учебные предметы, в рамках которых разрабатывался проект: математика, география, история, информатика.
— по виду деятельности – информационно-исследовательский;
— по организационной форме – групповой;
— по содержанию – межпредметный;
— по времени выполнения – долговременный.
4. Цель проекта: Изучить историю возникновения таких понятий как «географические координаты» и «метод координат» в математике. Проанализировав данные различных источников, сравнить эти понятия, выявить генетическую связь между ними, найти черты сходства и различия и отразить это в графических анализаторах. Получить информацию о практическом использовании данных понятий в нашей повседневной жизни.
— Познакомиться с историей развития наук, связанных с описанием поверхности Земли и измерениями на поверхности Земли.
— Выяснить, когда и в связи с чем понятие «координаты» впервые появилось в математике и какие ветви этой науки оно связало.
— Проанализировать и систематизировать полученную информацию, выявить черты сходства и различия между этими понятиями и отразить это в графических анализаторах: концептуальной карте и диаграмме Эйлера-Венна.
— Сделать компьютерную презентацию своей работы и представить ее на уроках математики и географии, а также на школьной научно-практической конференции.
6. Аннотация проекта: Данный проект направлен на углубление знаний по различным предметам школьной программы, формирование у детей понимания взаимосвязи и взаимозависимости между различными учебными дисциплинами, единства окружающего их мира, практического использования знаний, получаемых в школе, в повседневной жизни. Ребята работают в команде, учатся слушать и слышать как своих товарищей по команде, так и оппонентов, грамотно излагать свои мысли и уметь презентовать полученные результаты. При работе с графическими анализаторами они используют такие методы научного познания, как анализ и синтез. Работа над проектом позволяет понять и почувствовать роль и значение математики для решения насущных повседневных задач.