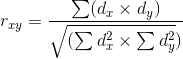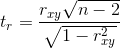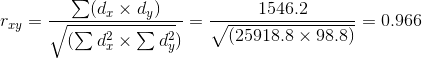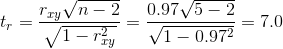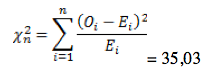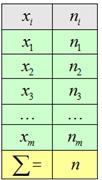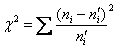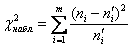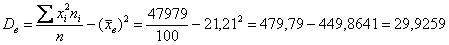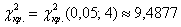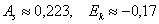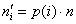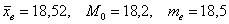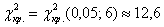для чего используют критерий пирсона
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Хи-квадрат (χ 2 ) Пирсона: условия применения метода и интерпретация
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами). Стоит отметить, что при работе с сопряженными таблицами хи-квадрат часто является поддержкой для анализа влияния факторов риска с помощью расчета рисков (абсолютный и относительный риски) и отношение шансов.
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
Четвертый этап
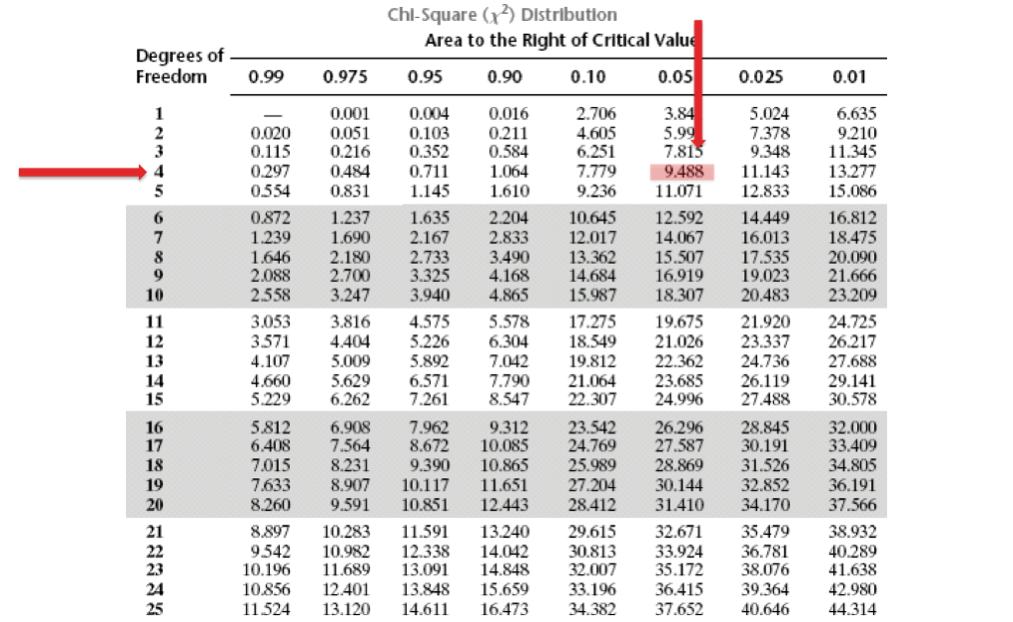
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата:
КРИТЕРИЙ ПИРСОНА: CУЩНОСТЬ И ПРИМЕНЕНИЕ МЕТОДА НА ПРАКТИКЕ
Данный критерий использует для расчета согласия эмпирического значения и предполагаемого, а также для расчета однородности двух независимых выборок.
Ограничения при использовании критерия Пирсона:
1. объем выборки должен быть больше 30 ();
2. теоретическая частота каждой ячейки таблицы не должна быть меньше 5 ();
3. выбранные разряды должны охватывать весь диапазон вариативности признаков;
4. разряды должны быть неперекрещивающимися.
Рассмотрим условие задачи. Необходимо сравнить два аналогичных товара, которые находятся в магазине. В этом магазине заранее было проведено добровольное анкетирование покупателей. В анкете был указан вопрос: какой товар вам понравился больше всего? Результаты опроса представлены в таблице 1.
Таблица 1. Результат проведенного опроса
Какой товар вам понравился больше всего?
Согласно условию, всего в опросе приняло 187 человек. Из них на долю 1-го магазина пришлось 42,8% (80 человек), а на долю 2-го магазина – 57,2% (107 человек).
Предположим, что уровень обслуживания в магазинах одинаков, тогда и доли довольных обслуживанием и недовольных обслуживанием будут такие же, как доли их представленности в общем числе опрошенных.
Всего 110 человек из 187 довольны обслуживанием в магазинах. Согласно высказанному предположению, 42,8% от этого числа должны прийтись на первый магазин – это составляет 47,06 от 110, а также 57,2% на 2-й магазин, что составит 62,94 от 110.
Данное рассуждение повторяем для покупателей не довольных обслуживанием. Их всего 77 человек. На 1-й магазин приходится 42,8% от этого числа, т.е. 32,94 от 77, а на долю 2-го магазина – 57,2%, т.е. 44,06 от 77.
Нулевая гипотеза имеет в данном раскладе тот смысл, что между покупателями нет различия при таком соотношений голосовавших.
Таблица 2. Распределение численности (частот) покупателей по магазинам
13. Гипотеза о законе распределения генеральной совокупности.
Критерий согласия Пирсона
Итак, после разгрома двух десятков задач ставим вишенку на торт статистических гипотез, а именно разбираем важнейшую гипотезу о виде (законе) распределения и распространённые тематические примеры.
Рассмотрим генеральную совокупность, распределение которой неизвестно. Однако есть основание полагать, что она распределена по некоторому закону 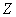
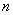
И нам требуется на уровне значимости 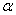
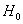
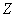
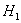
Как проверить эту гипотезу? Постараюсь объяснить кратко. Как вы знаете, выборочные данные группируются в дискретный или интервальный вариационный ряд с вариантами 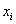
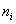
Поскольку эти данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты 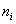
Далее строятся графики, рассчитываются выборочные характеристики (выборочная средняя 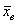
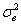
На основе некоторых выборочных характеристик по специальным формулам, которые зависят от проверяемого закона 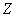
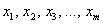
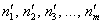
И возникает вопрос: значимо или незначимо различие между эмпирическими 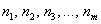
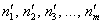
Для ответа на это вопрос рассматривают различные статистические критерии, которые называют критериями согласия, и наиболее популярный из них разработал Карл Пирсон:
При достаточно большом 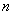
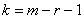
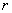
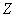
…всем понятно, почему величина 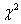
Далее строится правосторонняя критическая область: 
Критическое значение 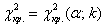
Наблюдаемое значение критерия рассчитывается по эмпирическим и найденным теоретическим частотам:
Если 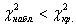
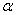
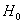
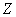
Если 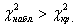
Обратите внимание на формулировку, которую я выделил жирным цветом – такая формулировка напоминает нам о том, что принятие статистической гипотезы ещё не означает её истинность, поскольку существует 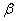
И, наконец, бараны коровы, которые нас уже заждались. Реалистичность фактических данных оставлю на совести автора методички сельскохозяйственной академии:
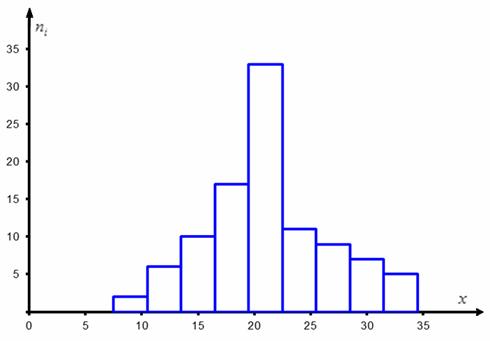
По результатам выборочного исследования найдено распределение средних удоев молока в фермерском хозяйстве (литров) от одной коровы за день:
На уровне значимости 0,05 проверить гипотезу о том, что генеральная совокупность (средний удой коров всей фермы) распределена нормально. Построить гистограмму частот и теоретическую кривую.
…если не любите молоко, то пусть это будет чай, сок, пиво или какой-то другой напиток, который вам нравится 🙂 Чтобы было интереснее исследовать эту волшебную ферму.
Решение: на уровне значимости 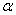
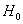
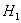
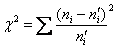
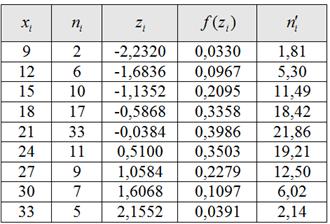
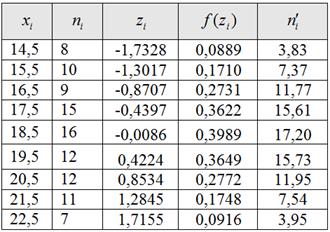
Эмпирические частоты известны из предложенного интервального ряда, и осталось найти теоретические. Для этого нужно вычислить выборочную среднюю 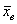
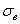
Выберем в качестве вариант 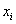
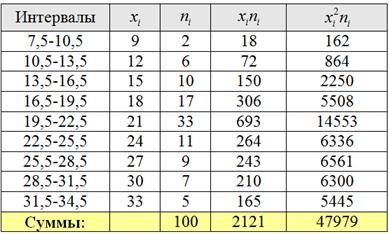
Внимание! Если вы не понимаете, как заполнять эту таблицу, или не знаете, как это сделать быстро, то обязательно обратитесь к Примеру 16, там есть все объяснения и видео!
Вычислим выборочную среднюю:
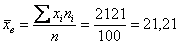
Выборочную дисперсию вычислим по формуле:
И выборочное стандартное отклонение:
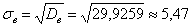
По причине большого объёма выборки его исправлением можно пренебречь.
Теоретические частоты рассчитываются по формуле: 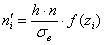
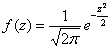
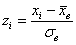
Входные данные известны: 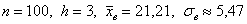
Все вычисления удобно проводить в Экселе и на всякий случай я распишу одну строчку:
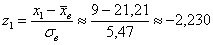
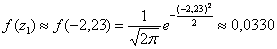
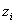
И, наконец, теоретическая частота: 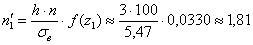
Надеюсь, на данный момент уже все умеют протягивать (копировать) формулы по образцу, а если нет, то я всё равно научу 🙂 Решил таки записать отдельный ролик, хотя особой технической новизны тут нет:

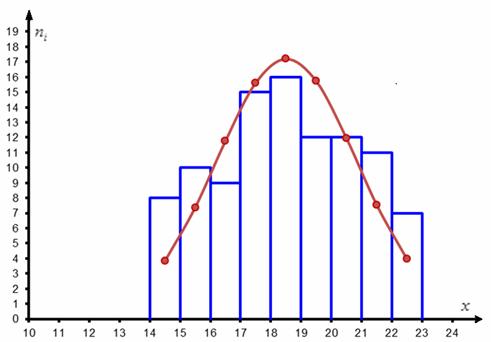
Построим гистограмму эмпирических частот и теоретическую кривую, которая проходит через точки 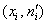
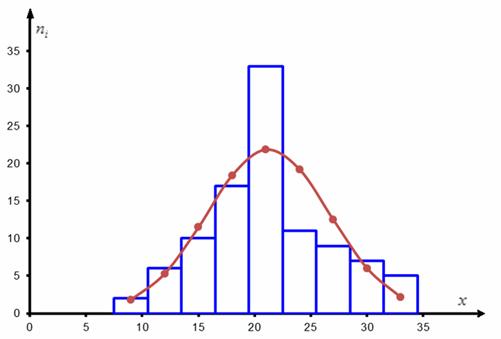
О технике построения гистограммы в MS Excel я рассказывал на уроке об интервальном ряде распределения, вот нужный ролик на Ютубе, и далее через правый клик к ней добавляется нормальная кривая. Эта кривая построена на основе выборочных данных (выборочной средней и стандартного отклонения) и наилучшим образом приближает гистограмму. Дальнейшая задача состоит в том, чтобы оценить, насколько ЗНАЧИМО отличаются эмпирические частоты (ступеньки гистограммы) от соответствующих теоретических частот (уровень коричневых точек).
Но перед тем, как сравнивать теоретические и эмпирические частоты, следует объединить интервалы с малыми (меньше пяти) частотами. В данном случае объединяем два первых и два последних интервала, для этого суммируем частоты, обведённые красным цветом, и получаем оранжевые результаты: 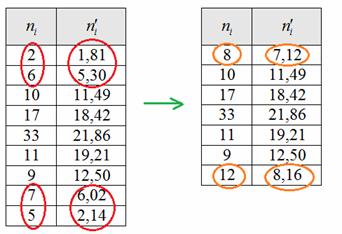
Это нужно для того, чтобы сгладить неоправданно большое расхождением между малыми частотами по краям выборки. Действие не обязательное, но крайне желательное, ибо студентов на моей памяти часто заставляли переделывать задание.
Найдём критическое значение 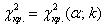
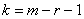
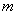
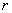
Так как мы объединяли интервалы, то теперь их не девять, а 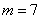
У нормального закона мы оцениваем 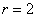
Пояснение: 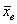
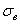
Таким образом, 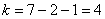
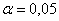
Это значение можно найти по таблице критических значений распределения хи-квадрат или с помощью Калькулятора (Пункт 11б).
При 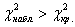
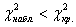

Вычислим наблюдаемое значение критерия 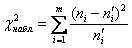
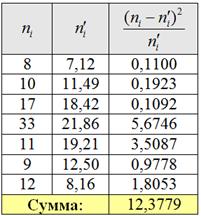
На всякий пожарный пример расчёта: 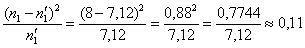
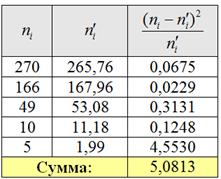
В нижней строке таблицы у нас получилось готовое значение 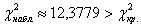
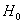
Иными словами различие между эмпирическими и теоретическими частотами статистически значимо и вряд ли объяснимо случайными факторами.
Ответ: на уровне значимости 0,05 гипотезу о нормальном распределении отвергаем
В чём может быть причина? Ведь по теореме Ляпунова большинство коров не оказывает практически никакого влияния на удой других коров, и поэтому распределение ген. совокупности должно быть близкО к нормальному.
Причины могут быть разными. Например, неоднородный состав совокупности (коровы разной породы), или на ферме есть VIP-хлев, где коровы получают улучшенное питание 🙂 А может быть, некоторые коровы больны и как раз оказывают существенное влияние на остальных, в связи с чем нарушается условие теоремы Ляпунова.
Интересно отметить, что при уменьшении уровня значимости до 0,01 критическое значение 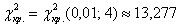
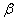
И, конечно, в случае сомнений имеет смысл увеличить объём выборки, чтобы провести повторное исследование.
Рассмотренная задача может встретиться в более простой или более сложной формулировке. В версии-«лайт» вам предложат готовые теоретические частоты, где остаётся только проверить гипотезу. Продвинутое же условие звучит примерно так:
На основании исследования выборки выдвинуть гипотезу о законе распределения генеральной совокупности
То есть, здесь не говорится о том, что предполагаемый закон нормальный (или какой-то другой) – этот вопрос вам предлагается проанализировать самостоятельно.
Каким образом это можно сделать?
Во-первых, гипотезу можно выдвинуть априорно, даже не исследуя выборку, и зависеть она будет от содержания задачи. Так, для коров используем упомянутую выше теорему Ляпунова: если каждый объект совокупности оказывает несущественное влияние на всю совокупность, то её распределение близкО к нормальному. Если речь идёт о погрешностях округления, то распределены они обычно равномерно. Если распадаются радиоактивные изотопы, то, скорее всего, по экспоненциальному закону. И так далее.
Но по условию, требуют опираться на выборочные данные, и здесь есть сразу несколько признаков, чтобы «вычислить» этот закон. Самый простой и наглядный способ – графический. Грубо говоря, чертим и смотрим. Интервальный вариационный ряд чаще всего изображают гистограммой, возвращаемся к нашим коровам:
Построенная гистограмма по форме напоминает колоколообразный график плотности нормального распределения, и это является веской причиной предположить, что генеральная совокупность распределена нормально. Да, здесь есть слишком высокий средний столбик, но, возможно, это просто случайность выборки.
Если столбики примерно одинаковы по высоте, то предполагаем, что генеральная совокупность распределена равномерно. Для показательного распределения тоже будет своя, характерная гистограмма.
Следующие признаки аналитические, приведу их для нормального распределения:
1) У нормального распределения математическое ожидание совпадает с модой и медианой. В нашем случае соответствующие выборочные показатели весьма близкИ друг к другу (матожидание оценивается выборочной средней):
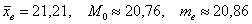

Желающие могут рассчитать моду и медиану самостоятельно. Впрочем, желающими часто становятся поневоле, поскольку задача, которую мы рассматриваем, нередко идёт в комплексе со всеми этими заданиями.
2) Выполнение правила «трёх» сигм. Практически все значения нормальной случайной величины находятся в интервале 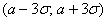
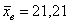
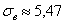
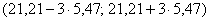
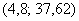
3) Коэффициенты асимметрии и эксцесса нормального распределения равны нулю. В нашем случае эти характеристики не сказать что сильно, но довольно близкИ к нулю:
На практике в исследование желательно включить все пункты за исключением, возможно, третьего (т.к. асимметрию и эксцесс рассчитывают далеко не всегда).
Следует отметить, что перечисленные выше предпосылки ещё не означают, что распределение нормально или то, что соответствующая гипотеза будет принята. В чём мы недавно и убедились.
И теперь настал момент продолжить решение нашего «экзаменационного» задания:
Если вы не прорешали предыдущие пункты, то настоятельно рекомендую это сделать, ну или просто взять готовые числа из образца:
6) По найденным характеристикам сделать вывод о законе эмпирического ряда распределения.
7) Построить нормальную кривую по опытным данным на графике гистограммы.
8) Произвести оценку степени близости теоретического распределения эмпирическому ряду с помощью критерия согласия Пирсона на уровне значимости 0,05.
Как видите, Пункт 6 как раз на обоснование предполагаемого закона распределения. Краткое решение в конце этого урока.
И, конечно же, ещё одна задача, передаю привет студентам Университета путей сообщения:
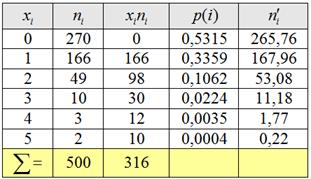
В результате проверки 500 контейнеров со стеклянными изделиями установлено, что число повреждённых изделий 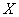

( 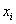
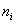
С помощью критерия согласия Пирсона на уровне значимости 0,05 проверить гипотезу о том, что случайная величина 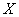
…здесь тоже представьте изделия по своему интересу 🙂
Все числа уже забиты в макет, придерживайтесь следующего алгоритма:
1) Находим выборочную среднюю 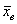
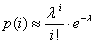
2) Находим значения 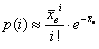
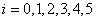
3) Находим теоретические частоты
4) Находим критическое значение 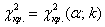
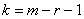
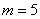
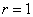
5) Рассчитываем наблюдаемое значение критерия 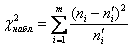
Примерный образец чистового оформления задачи в конце урока.
Помимо разобранных примеров, в задачнике В. Е. Гмурмана можно найти аналогичные задачи для биномиального, равномерного и показательного распределения, но лично в моей практике они почти не встречались.
Желаю успехов и до скорых встреч!
Пример 20. Решение (продолжение):
6) Проанализируем полученные результаты:
Форма гистограммы похожа на нормальную кривую.
Выборочная средняя, мода и медиана достаточно близкИ друг другу:
Построим интервал 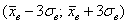
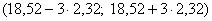
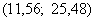
Асимметрия практически равна нулю 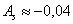
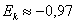
Перечисленные признаки позволяют предположить, что генеральная совокупность распределена нормально.
7) Найдём теоретические частоты: 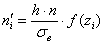
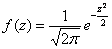
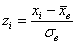
в данной задаче 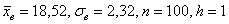
Построим гистограмму частот и теоретическую кривую:
8) Проверим гипотезу 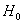
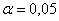
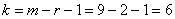
При 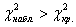
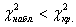
Вычислим наблюдаемое значение критерия 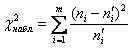
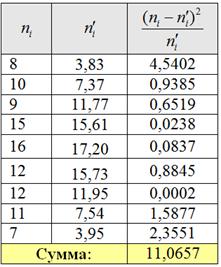
В результате: 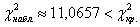
Пример 54. Решение: проверим гипотезу 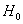
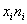
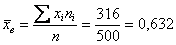
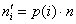
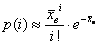
Вычисления сведём в таблицу:
Объединяем две последние варианты ввиду их малых частот и находим критическое значение для уровня значимости 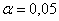
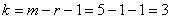
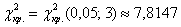
Вычислим наблюдаемое значение критерия 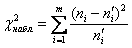
Таким образом, 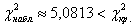
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5