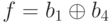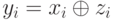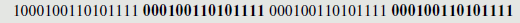для чего используются в криптографии сдвиговые регистры с обратной связью
В поисках криптостойкого ГПСЧ
В сегодняшнем посте речь пойдет о криптостойкости генераторов псевдослучайных чисел (ГПСЧ).
Для начала определимся, что же такое криптостойкий ГПСЧ (КСГПСЧ).
КСГПСЧ должен удовлетворять «тесту на следующий бит». Смысл теста в следующем: не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 битов с вероятностью более 50 %.
Возможно, кое-кто из читателей использовал такие ГПСЧ, как регистры сдвига с линейной обратной связью (РСЛОС) или любимый многими программистами Вихрь Мерсенна. Я постараюсь показать, что оба этих способа, несмотря на весьма хорошие статистические свойства и большие периоды, не соответствуют приведенному выше определению и их нельзя считать криптографически стойкими, а также предложу, в качестве альтернативы, два очень надежных ГПСЧ.
Регистр сдвига с линейной обратной связью
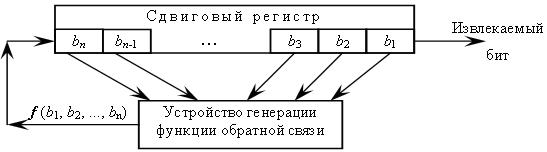
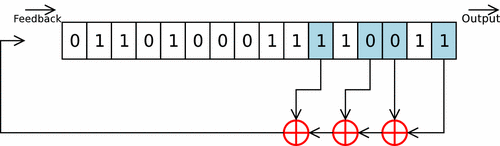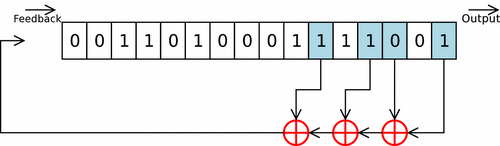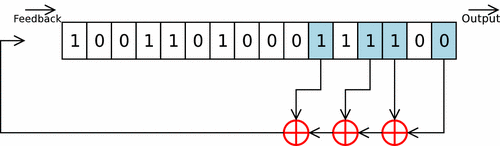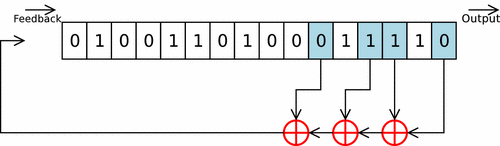
Часто доводилось видеть как этот метод предлагали использовать в криптографических целях, поэтому, с него, собственно, и начнем. Такого рода генераторы состоят из сдвигового регистра и функции обратной связи.
Каждый ГПСЧ на РСЛОС связан с определенным многочленном, который характеризует длину регистра и функцию обратной связи. К примеру, многочлену соответствует следующий регистр:
Степень многочлена задает длину регистра, ненулевые члены описывают какие элементы регистра составляют отводную последовательность.
Если многочлен образующий отводную последовательность является неприводимым по модулю 2, тогда период генерируемой регистром последовательности будет максимальным и вычисляется по формуле .
Перед началом работы в регистр заносится произвольная последовательность бит, которая называется начальным состоянием. После чего каждый такт генератора возвращает 1 бит, выглядящий совершенно случайным.
Сами по себе РСЛОС являются хорошими ГПСЧ, но в силу того, что полученные с их помощью биты имеют линейную связь использовать РСЛОС в криптографических целях неразумно.
Если злоумышленник получит последовательность бит длиной n, сгенерированную с помощью РСЛОС он может загрузить эти биты в регистр и прокрутив его назад получит начальное состояние. Знание начального состояния даст ему доступ ко всем сгенерированным раннее и генерируемым в будущем последовательностям.
На вход поступает последовательность бит, сгенерированная с помощью РСЛОС. В качестве результата возвращается многочлен, характеризующий схему обратной связи.
Разумеется, РСЛОС можно объединять в каскады для более криптостойкого ГПСЧ. Эта идея используется в некоторых поточных шифрах. Однако, многие генераторы, основанные на этом способе уязвимы к так называемым корреляционным атакам. Немного подробностей об этом виде атак я приводил в своем недавнем посте Безопасность GSM сетей: шифрование данных. Здесь же скажу только, что с помощью корреляционной атаки, злоумышленник обладая последовательностью сгенерированной ГПСЧ имеет возможность восстановить начальное значение и получить доступ ко всем генерируемым в будущем значениям.
Вихрь Мерсенна
Гораздо более интересным на мой взгляд является ГПСЧ, называемый Вихрь Мерсенна. Существует несколько вариантов алгоритма, Мы рассмотрим только наиболее часто используемый MT19937. Кратко опишем этот алгоритм.
Вихрь Мерсенна состоит из двух частей: РСЛОС и закалки.
Регистр сдвига состоит из 624 элементов, каждый длиной 32 бита. Инициализация начального состояния описывается функцией:
На вход инициализационной функции подается некое значение seed, с помощью которого осуществляется заполнение всего регистра.
На первом и каждом последующем 624-м шаге происходит перемешивание внутреннего состояния регистра:
На каждом шаге алгоритм возвращает следующее число из текущего состояния регистра и производит так называемую «закалку»:
Для того чтобы получить доступ к внутреннему состоянию алгоритма атакующему достаточно получить последовательность состоящую из 624 чисел.
Все что нужно сделать это вернуть числа сгенерированные алгоритмом к состоянию, в котором они находились до этапа «закалки». Для этого необходимо проделать все шаги закалки в обратном направлении. Например, рассмотрим последний шаг закалки:
y := y ^ (y >>> 18)
Давайте посмотрим что происходит с двоичными данными при выполнении этой операции:
y 101101110101111001 11111001110010
y >>> 18 00000000000000000010110111010111 100111111001110010
y ^ (y >>> 18) 101101110101111001 01001110100101
Как видите, первые 18 бит результата и исходного числа совпадают. Для того чтобы восстановить оставшиеся 14 бит нам нужно проделать следующее действие:
result ^ (result >>> 18)
Действуя аналогичным образом для всех шагов этапа закалки мы получим элемент начального состояния ГПСЧ:
Как я уже отмечал выше, если атакующий имеет 624 числа сгенерированных с помощью Вихря Мерсенна этого достаточно для того чтобы восстановить все внутреннее состояние и предугадывать с вероятностью 100% все генерируемые в последующем числа.
Криптостойкие ГПСЧ
В качестве альтернативы я хочу предложить два очень надежных метода.
Принцип работы РСЛОС
Введение
Регистр сдвига с линейной обратной связью (РСЛОС, англ. Linear Feedback Shift Register, LFSR) — сдвиговый регистр битовых слов, у которого значение входного бита однозначно задается некоторой функцией, исходя из значений остальных битов регистра до сдвига. Регистр сдвига может представлять собой некоторую электрическую схему, составленную из дискретных компонентов: транзисторов, резисторов, также может быть интегрирован в микросхему или же реализован в программе. Добавление обратной связи превращает регистр сдвига в генератор псевдослучайных чисел, который находит широкое применение в криптографии. В статье мы разберем принцип работы РСЛОС от hardware до различных его применений.
Регистр, в общем случае – это схема, состоящая из связанных между собой однобитовых элементов памяти. Такие схемы умеют записывать, хранить, считывать n-разрядные двоичные данные. В статье рассматривается вид регистра, называемый регистром сдвига. Чаще всего регистр сдвига собирается на основе последовательно соединенных D-триггеров, притом количество этих триггеров равно числу разрядов n. С принципов работы D-триггера мы и начинаем статью.
D-триггер
Кратко затронем самые основы. Глобально, электронику можно разделить на два раздела: аналоговый и цифровой. Принципиальная особенность второго заключается в том, что сигналы задаются дискретными уровнями напряжения. Притом дискретных уровня всего два. Таким образом, вместо того, чтобы записывать напряжение в вольтах, достаточно просто называть один из двух дискретных уровней. Так и появляются названия «ноль» и «единица». В действительности, они определяют некоторые уровни напряжения, которые могут быть какими угодно. Хотя, в большинстве случаев, «ноль» обозначает уровень 0 Вольт, а «единица» уровень 5 В, 3.3 В, 1.8 В, 1.5 В и т.д. Таким образом, фраза «на входе ноль, на выходе единица» обозначает: «на входе напряжение, соответствующее уровню ноль, на выходе напряжение, соответствующее уровню единица».
Двигаемся далее. Теперь у нас есть цифровой сигнал, что же интересного можно с ним сделать? Подать на D-триггер и посмотреть, что будет! Но сначала дадим пару определений.
Триггер – электронное устройство, обладающее способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов.
D-триггер – триггер, сохраняющий состояние входа. Притом, это состояние отображается на выходе
На электрической схеме устройства D-триггер выглядит ровно так же, как на рисунке ниже. Такой вид триггера обязательно имеет три вывода: D (вход), C (вход синхронизации, вход тактирования, тактовый вход, clk, clock) и Q (выход). Помимо них могут иметься еще: инвертированный выход, входы сброса и установки значения на выходе, вход разрешения работы. Однако, суть работы заключается именно во взаимодействии трех обязательных выводов, поэтому именно их мы и рассмотрим.
Принцип работы D-триггера следующий: при подаче тактового сигнала на вход C, состояние на выходе становится равным состоянию на входе. Т. е. если в какой-то момент времени на входе был «ноль», а на выходе «единица», то в момент подачи тактового сигнала выход примет состояние входа и станет «нулём».
Поточные шифры и генераторы псевдослучайных чисел. Часть 2
Генераторы псевдослучайных чисел на основе сдвиговых регистров с обратной связью
Поточные шифры с использованием сдвиговых регистров достаточно долго использовались на практике. Это связано с тем, что они очень хорошо реализуются с помощью цифровой аппаратуры.
Простейшим видом сдвигового регистра с обратной связью является линейный сдвиговый регистр с обратной связью ( linear feedback shift register – LFSR ). Обратная связь в этом устройстве реализуется просто как сумма по модулю 2 всех (или некоторых) битов регистра. Биты, которые участвуют в обратной связи, образуют отводную последовательность. Линейные сдвиговые регистры с обратной связью или их модификации часто применяется в криптографии.
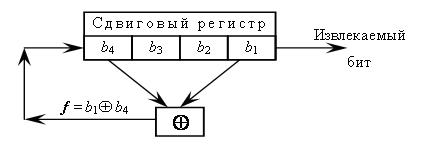
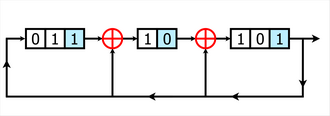
Для того, чтобы стало понятнее, как работает сдвиговый регистр с обратной связью, рассмотрим 4-битовый LFSR с отводом от первого и четвертого разрядов, представленный на рис. 8.2.
| Номер состояния | Внутреннее состояние регистра b4, b3, b2, b1 | Результат вычисления функции обратной связи
| Извлекаемый бит ( b1 ) |
|---|---|---|---|
| 0 | 1 0 1 1 | 0 | 1 |
| 1 | 0 1 0 1 | 1 | 1 |
| 2 | 1 0 1 0 | 1 | 0 |
| 3 | 1 1 0 1 | 0 | 1 |
| 4 | 0 1 1 0 | 0 | 0 |
| 5 | 0 0 1 1 | 1 | 1 |
| 6 | 1 0 0 1 | 0 | 1 |
| 7 | 0 1 0 0 | 0 | 0 |
| 8 | 0 0 1 0 | 0 | 0 |
Основным недостатком генераторов псевдослучайных чисел на базе линейных сдвиговых регистров является сложность программной реализации. Сдвиги и битовые операции легко и быстро выполняются в электронной аппаратуре, поэтому в разных странах выпускаются микросхемы и устройства для поточного шифрования на базе алгоритмов с использованием сдвиговых регистров с обратной связью.
Использование режимов OFB и CTR блочных шифров для получения псевдослучайных чисел
Название режима OFB ( Output FeedBack ) переводится как » обратная связь по выходу».
Таким образом, для получения псевдослучайной последовательности используется схема:
Последовательность чисел zi можно использовать в качестве гаммы для шифрования потока исходных данных, состоящего из символов хi :
Основное достоинство режима OFB заключается в том, что последовательность z может быть сформирована заранее для того, чтобы быстро шифровать или расшифровывать поточные сообщения в момент их поступления. Это может быть актуально для систем, обрабатывающих данные в реальном масштабе времени.
Это дает возможность шифровать и дешифровать любые фрагменты сообщения независимо друг от друга.
Регистр сдвига линейной обратной связи
Спектр приложений очень широк: шифрование коммуникаций, проверка ошибок при передаче данных, самотестирование электронных компонентов и т. Д.
Резюме
Операция
Принцип
Пример
| Часы | Статус LFSR | Выход |
|---|---|---|
| 0 | 0 1 1 0 | |
| 1 | 1 0 1 1 | 0 |
| 2 | 0 1 0 1 | 1 |
| 3 | 0 0 1 0 | 1 |
| 4 | 0 0 0 1 | 0 |
| 5 | 1 0 0 0 | 1 |
| 6 | 1 1 0 0 | 0 |
| 7 | 0 1 1 0 | 0 |
Пример последовательных состояний 4-битного LFSR с подключением первой, второй и четвертой ступеней на уровне функции обратной связи:
На седьмом тактовом импульсе состояние регистра идентично его исходному состоянию. LFSR считается периодом 7.
Математические модели
Дизайн
Определения
Созданный люкс Последовательность, сгенерированная этим LFSR, является последовательностью, проверяющей рекуррентное отношение ( в нет ) нет ∈ НЕТ <\ Displaystyle (а_ <п>) _ <п \ в \ mathbb 
Полиномиальные представления
Периодичность
Алгоритм Берлекампа-Месси
Режимы подключения
Представление, используемое до сих пор для представления связи между различными этапами регистра, описывает так называемый режим «Фибоначчи». Возможно другое представление, используя так называемый режим «Галуа».
Фибоначчи
Регистр в режиме Фибоначчи строго применяет определение LFSR: содержимое различных этапов добавляется или не добавляется друг к другу, результат этого добавления затем помещается во входной этап регистра, и все этапы претерпевают сдвиг в сторону выход.
Галуа
В так называемом режиме Галуа содержимое выходного каскада добавляется или не добавляется к содержимому каскадов регистра, тогда все каскады претерпевают сдвиг в сторону выхода, а содержимое выходного каскада повторно вводится в каскад. Вход.
На аппаратном уровне LFSR часто реализуются с использованием этого режима, поскольку он быстрее и имеет меньшую задержку, чем режим Фибоначчи, поскольку этапы обновляются одновременно.
Приложения
LFSR существуют в двух формах: аппаратном и программном, но это прежде всего первая конфигурация, которая используется, потому что она проста в реализации (недорогое оборудование, связанное с простым алгоритмом обработки).
Использование этой технологии можно найти в следующих областях:
Генерация псевдослучайных чисел
Было много публикаций о генерации псевдослучайных чисел с помощью регистров сдвига, и из некоторых исследований регистров с нелинейной обратной связью (в) большинство авторов используют линейную обратную связь.
Фундаментальной проблемой в криптологии является создание «как можно более случайных» битовых строк. Ярким примером является генерация ключей шифрования ( симметричных или асимметричных ).
Эта проблема фактически распадается на две части:
Шифрование данных
Криптография
LFSR являются основными компонентами многих генераторов шифров.
Причины, по которым LFSR используются в большом количестве генераторов потока, следующие:
Однако использование LFSR в их начальных конфигурациях очень быстро стало уязвимым для математических атак (продемонстрировано алгоритмом Берлекампа-Месси ).
Чтобы не быть уязвимой, компьютерная система должна быть защищена от известных и упоминаемых атак, поэтому LFSR никогда не должен использоваться сам по себе в качестве генератора потока ключей.
Тем не менее, LFSR все еще используются из-за очень низкой стоимости внедрения.
Чтобы обойти влияние свойств линейности LFSR, можно использовать три метода:
Ожидаемые свойства генератора зашифрованного потока:
Примеры криптографических алгоритмов с использованием LFSR:
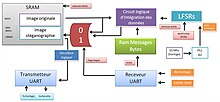
Стеганография
Псевдослучайные последовательности на основе LFSR являются одним из методов шифрования информации.
Обнаружение ошибок и исправление данных
| Заявление | Тип | размер LFSR |
|---|---|---|
| CRC | CRC-12 | 12 |
| CRC-16 | 16 | |
| Сеть банкоматов | CRC-32 | 32 |
Этот механизм, который называется циклическим контролем избыточности и который мы находим под названием CRC, представляет собой устройство контроля ошибок во время передачи необработанных данных в сетевом домене, цифровом хранилище или даже при сжатии данных.
Самопроверка электронных схем
Случайные тесты части компонента предполагают возможность воздействовать на выборку данных компонента.
Цифровая обработка сигналов
Это исследование обработки оцифрованного сигнала, такого как фильтрация или сжатие, оно обеспечивается процессором цифрового сигнала, который можно найти в этом поле с помощью DSP. Эти операции было бы трудно выполнять непосредственно с двоичными данными в памяти без алгоритма сжатия / распаковки.
LFSR часто используются для этой задачи, поскольку они эффективны при обработке больших объемов двоичных данных и имеют низкую стоимость реализации в их аппаратной форме.
Счетчики на основе LFSR
Другое использование LFSR
Примечания и ссылки
Заметки
Рекомендации
Библиография
Руководства и курсы
Научно-исследовательские работы
Введение в основы современных шифров с симметричным ключом
7.2. Современные шифры потока
Синхронные шифры потока
В синхронном шифре потока ключевой поток независим от потока зашифрованного текста или исходного текста. Ключевой генерируемый поток не используется без отношений между ключевыми битами и исходным текстом или битами зашифрованного текста.
Одноразовый блокнот
Какой вид имеет зашифрованный текст при использовании шифра одноразового блокнота в каждом из следующих случаев?
а. Исходный текст состоит из n нулей.
б. Исходный текст состоит из n единиц.
в. Исходный текст состоит из чередующихся нулей и единиц.
г. Исходный текст — случайная строчка бит.
a. Поскольку 
, то поток зашифрованного текста совпадет с ключевым потоком. Если ключ случайный, зашифрованный текст также случайный. Отрывки исходного текста в зашифрованном тексте не сохраняются.
b. Поскольку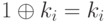 
, где 
является дополнением, поток зашифрованного текста — дополнение ключевого потока. Если ключевой поток случайный, то зашифрованный текст также случайный, отрывки исходного текста не сохраняются в зашифрованном тексте.
c. В этом случае каждый бит в потоке зашифрованного текста является или тем же самым, что и в ключевом потоке, или его дополнением. Поэтому результат — также случайный, если ключевой поток случайный.
d. В данном случае зашифрованный текст явно случайный, потому что проведение операции ИСКЛЮЧАЮЩЕЕ ИЛИ двух случайных битов в результате дает случайный поток бит.
Регистр сдвига с обратной связью
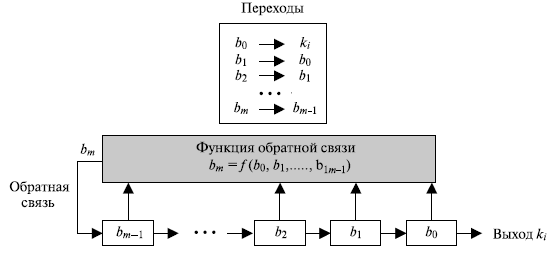
Одно усовершенствование к одноразовому блокноту — Регистр сдвига с обратной связью ( FSR — Feedback Shift Register ). FSR может быть реализован или в программном обеспечении, или в аппаратных средствах, но для простоты мы рассмотрим аппаратную реализацию. Регистр сдвига с обратной связью состоит из регистра сдвига и функции обратной связи, как показано на рис. 7.23.
Рисунок 7.25 показывает схему и использование линейного регистра сдвига с обратной связью для шифрования.
Таблица 7.6. показывает значение потока ключей. Для каждого перехода первое значение b4 вычисляется, а затем каждый бит сдвигается на одну ячейку вправо.
| Текущее значение | b4 | b3 | b2 | b1 | b0 | ki |
|---|---|---|---|---|---|---|
| Начальное значение | 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 0 | 1 | 1 | 0 |
| 8 | 1 | 0 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 0 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 0 | 1 | 0 |
| 11 | 1 | 1 | 1 | 1 | 0 | 1 |
| 12 | 0 | 1 | 1 | 1 | 1 | 0 |
| 13 | 0 | 0 | 1 | 1 | 1 | 1 |
| 14 | 0 | 0 | 0 | 1 | 1 | 1 |
| 15 | 1 | 0 | 0 | 0 | 1 | 1 |
| 16 | 0 | 1 | 0 | 0 | 0 | 1 |
| 17 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 1 | 0 | 0 | 1 | 0 | 0 |
| 19 | 1 | 1 | 0 | 0 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 | 0 | 1 |
Атаки шифров, полученных с помощью линейных регистров сдвига с обратной связью.Линейный регистр сдвига с обратной связью имеет очень простую структуру, но эта простота делает шифр уязвимым к атакам. Два общих типа атаки приведены ниже.
Однако нелинейный регистр сдвига с обратной связью не имеет общего характера, поскольку нет математического обоснования, как получить такой регистр с максимальным периодом.
Можно применить линейный регистр сдвига с обратной связью с максимальным периодом и затем скомбинировать его обратную связь с помощью нелинейной функции.
Несинхронные шифры потока
В несинхронном шифре потока каждый ключ в ключевом потоке зависит от предыдущего исходного текста или зашифрованного текста.
Два метода, которые используются, чтобы создать различные режимы работы для блочных шифров ( режим обратной связи по выходу и режим счета сцеплений блоков шифра ), фактически создают шифры потока (см. «Шифрование, использующее современные шифры с симметричным ключом» ).