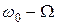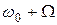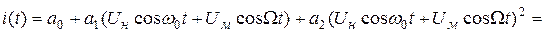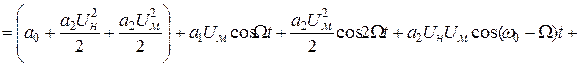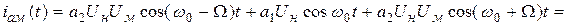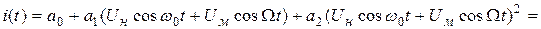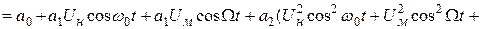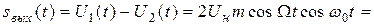для чего нужен амплитудный модулятор
Амплитудная модуляция на пальцах
В недавней статье «Амплитудная модуляция произвольного сигнала» её автор довольно сумбурно попытался представить своё понимание формирования спектра при амплитудной модуляции. Но отсутствие иллюстраций и избыток математики с привлечением интегральных преобразований помешало сообществу понять мысли автора и оценить статью по достоинству; в то время как тема это достаточно простая — и рассмотреть которую мы попробуем ещё раз, на этот раз с картинками и привлечением Wolfram Mathematica.
Итак, идея амплитудной модуляции состоит в том, чтобы передавать низкочастотный сигнал — голос или музыку — модулируя высокочастотный (несущий) сигнал, многократно превышающий слышимый диапазон и занимающий узкую полосу частот в радиоэфире. Сама модуляция осуществляется простым умножением сигнала на несущий:
Здесь у нас в качестве несущей выступает синусоида с частотой 5:
А сам сигнал — с частотой 1:
Можно заметить, что сигнал смещён вверх и имеет только положительные значения. Это не случайно и является обязательным условием для возможности последующего его корректного восстановления. Как же его восстановить? Очень просто! Нужно сдвинуть фазу промодулированного сигнала на 90 градусов (операция, известная как преобразование Гильберта), и посчитать корень из суммы квадратов модулированного и преобразованного сигналов:
В более простом (но грубом) варианте преобразование Гильберта можно заменить задержкой сигнала на четверть периода несущий частоты, а итоговый сигнал дополнительно отфильтровать фильтром низких частот. В ещё более простом варианте можно вообще не считать корней и квадратов, а отфильтровать сигнал по абсолютному значению (что и применяется обычно в радиоприёмниках).
Теперь посмотрим, что у нас происходит со спектрами. Посчитаем преобразование Фурье от несущей:
Так как дельта-функция Дирака не является функцией в классическом смысле, её график нельзя построить стандартным способом; поэтому сделаем это вручную, используя общепринятое начертание:
Ожидаемо получили ту же частоту, что и в начальной формуле. Наличие ещё одной такой же частоты, но со знаком минус, не случайно — это явление называется Hermitian symmetry и является следствием того, что рассматриваемая функция сугубо действительная и в комплексном представлении имеет нулевую мнимую компоненту. Отсутствие мнимых компонент в спектре после преобразования обусловлено тем, что изначально наши функции ещё и чётные (симметричные относительно нуля).
Теперь сделаем преобразование Фурье для самого сигнала:
Здесь мы дополнительно получили дельта-функцию Дирака в центре координат — вследствие наличия в сигнале постоянной составляющей, которая не имеет колебаний по определению — что позволяет её рассматривать как нулевую частоту.
Что же будет со спектром, если их перемножить? Посмотрим:
Из теории мы знаем, что умножение во временном домене равносильно свертке в частотном (и наоборот, что широко используется при FIR-фильтрации). А поскольку один из подвергаемых свёртке сигналов состоял только из одной (положительной и отрицательной) частоты, то в результате свёртки мы получили просто линейный перенос сигнала вверх по частоте (в обе стороны). И так как симметрия осталась, сигнал у нас по-прежнему не имеет мнимой компоненты.
Приведём его теперь к комплексному (аналитическому) виду, обнулив отрицательную область частот:
и сделаем обратное преобразование Фурье:
Так как функция теперь комплексная, для построения её графика необходимо отдельно извлечь действительную и мнимую компоненты:
Теперь у нашего сигнала появилась мнимая компонента, представляющая собой сдвинутый на 90 градусов исходный сигнал. Это будет более очевидным, если представить полученную функцию в тригонометрическом виде:
Пока не очень очевидно. Попробуем упростить:
Теперь больше похоже на правду — и как видим, функция нашего исходного сигнала тоже упростилась. Попробуем её вернуть к оригинальному виду:
Множитель 1/2 появился не случайно — ведь обнулив половину спектра, мы соответственно и уменьшили мощность сигнала. Ну а теперь, имея модулированный комплексный сигнал, мы можем взять и этот модуль посчитать:
Модуль комплексного числа как раз и считается через корень суммы квадратов мнимого и действительных компонентов. И отсюда понятно, почему кодируемый сигнал должен состоять только из положительных значений — если он будет включать отрицательные значения, то после восстановления они также станут положительными, что и называется перемодуляцией:
Восстановление сигнала также возможно и при помощи квадратурного гетеродина — когда модулированный сигнал снова умножается на несущую частоту, но на этот раз — комплексную:
За счёт того, что комплексная частота в частотной области имеет только один импульс без дублирования его в отрицательной области частот — то в результате свёртки мы получим линейный перенос спектра, при которой отрицательная часть спектра встанет обратно в центр, а положительная — сдвинется ещё дальше, и её останется только отфильтровать фильтром нижних частот.
Заключение
Как видим, в рассмотрении амплитудной модуляции через преобразовании Фурье нет ничего сложного; если же рассматривать её исключительно на школьном уровне, то достаточно вспомнить, что произведение (несущей) суммы (представление сигнала в виде тригонометрического ряда) равнозначно сумме произведений (каждого члена ряда по отдельности на несущую частоту) — и, соответственно, каждое такое произведение раскладывается на сумму двух синусоид по уже озвученной автором исходной статьи формуле.
Внимательный читатель также мог заметить, что раз в результате модуляции мы получили симметричный относительно несущей частоты спектр — значит, имеет место быть избыточность данных и можно оставить только одну боковую полосу, сократив тем самым занимаемую полосу частот в радиоэфире. Такая технология действительно имеется, но это — уже совсем другая история.
Теория радиоволн: аналоговая модуляция
Амплитудная модуляция
При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.
Данный спектр свойственен для модулирующего колебания постоянной частоты.
На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции
Амплитудная модуляция



Общие сведения об амплитудной модуляции
Амплитудная модуляция – это процесс формирования амплитудно-моду-лированного сигнала, т.е. сигнала, амплитуда которого изменяется по закону модулирующего сигнала (передаваемого сообщения). Этот процесс реализуется амплитудным модулятором.
Амплитудный модулятор должен формировать высокочастотное колебание, аналитическое выражение для которого в общем случае имеет вид
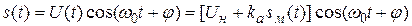
где 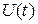
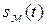
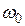
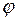
Для получения такого сигнала необходимо осуществить перемножение высокочастотного (несущего) колебания 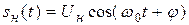
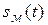
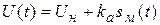
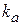
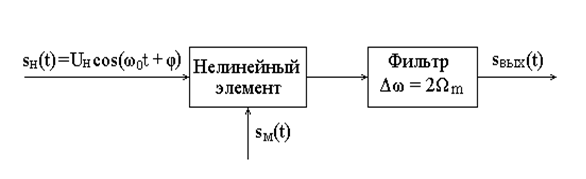
Структура амплитудного модулятора в случае использования нелинейного элемента представлена на рис. 8.4.
Рис. 8.4. Структурная схема амплитудного модулятора
Нелинейный элемент осуществляет преобразование несущего колебания и модулирующего сигнала, в результате чего формируется ток (или напряжение), в спектре которого содержатся составляющие в полосе частот от 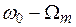
Перемножение двух сигналов можно осуществить с помощью нелинейного элемента, характеристика которого аппроксимируется полиномом, содержащим квадратичный член. Благодаря этому формируется квадрат суммы двух сигналов, содержащий их произведение.
Суть сказанного и общую идею формирования амплитудно-модулированного колебания иллюстрируют достаточно простые математические преобразования в предположении, что осуществляется тональная (одной частотой) модуляция.
1. В качестве нелинейного элемента используем транзистор, ВАХ которого аппроксимируется полиномом второй степени 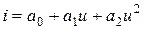
2. На вход нелинейного элемента подается напряжение, равное сумме двух колебаний: несущего и модулирующего, т.е.
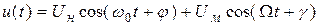
Начальные фазы колебаний будем считать в дальнейшем равными 0, т.к. их величины не имеют принципиального значения для понимания процесса амплитудной модуляции.
3. Спектральный состав тока определяется следующим образом:
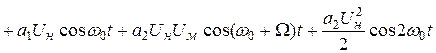
В полученном выражении спектральные составляющие расположены в порядке возрастания их частот. Среди них имеются составляющие с частотами 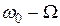
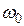
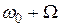

где 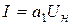
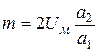
В передающих устройствах обычно совмещают процессы модуляции и усиления, что обеспечивает минимальные искажения модулированных сигналов. С этой целью амплитудные модуляторы строят по схеме резонансных усилителей мощности, в которых изменение амплитуды высокочастотных колебаний достигается изменением положения рабочей точки по закону модулирующего сигнала.
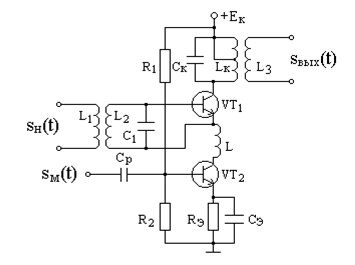
Схема и режимы работы амплитудного модулятора
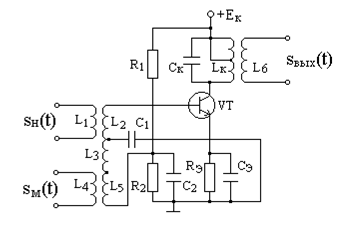
Схема амплитудного модулятора на основе резонансного усилителя представлена на рис. 8.5.
Рис. 8.5. Схема амплитудного модулятора на основе резонансного усилителя
На вход резонансного усилителя, работающего в нелинейном режиме, подаются:
несущее колебание 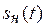
модулирующий сигнал 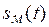
Конденсаторы 
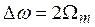
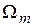
Выбором рабочей точки определяется режим работы модулятора. Возможны два режима: режим малых и режим больших сигналов.
а. Режим малых входных сигналов
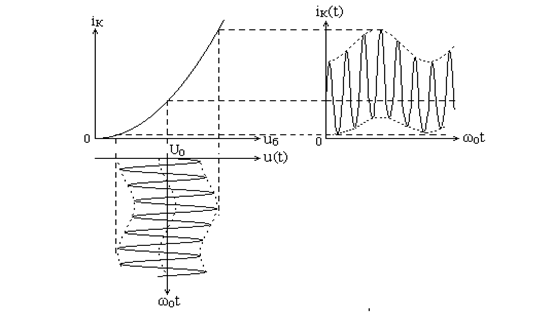
Этот режим устанавливается выбором рабочей точки в середине квадратичного участка ВАХ транзистора. Выбором амплитуды несущего колебания обеспечивается работа модулятора в пределах этого участка (рис. 8.6).
Рис. 8.6. Режим малых входных сигналов амплитудного модулятора
Амплитуда напряжения на колебательном контуре, резонансная частота которого равна несущей частоте, определяется амплитудой первой гармоники тока, т.е. 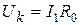
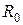
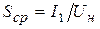
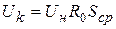
Под воздействием модулирующего напряжения, подаваемого на базу транзистора, будет изменяться положение рабочей точки, а значит, будет изменяться и средняя крутизна ВАХ. Так как амплитуда напряжения на колебательном контуре пропорциональна средней крутизне, то для обеспечения амплитудной модуляции несущего колебания необходимо обеспечить линейную зависимость крутизны от модулирующего сигнала. Покажем, что это возможно при использовании рабочего участка ВАХ, аппроксимируемого полиномом второй степени.
Итак, в пределах квадратичного участка ВАХ, описываемого полиномом, существует входное напряжение, равное сумме двух колебаний: несущего и модулирующего, т.е.
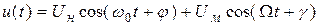
Начальные фазы колебаний будем считать в дальнейшем равными 0, т.к. их величины не имеют принципиального значения для понимания процесса амплитудной модуляции.
Спектральный состав тока коллектора определяется следующим образом:
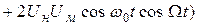
Выделяем первую гармонику тока:
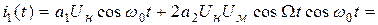
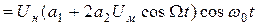
Таким образом, амплитуда первой гармоники равна:
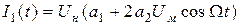
Как видно из полученного выражения, амплитуда первой гармоники тока линейно зависит от модулирующего напряжения. Следовательно, средняя крутизна также будет линейно зависеть от модулирующего напряжения.
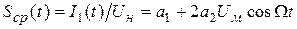
Тогда напряжение на колебательном контуре будет равно:
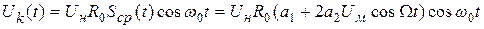
Следовательно, на выходе рассматриваемого модулятора формируется амплитудно-модулированный сигнал вида:
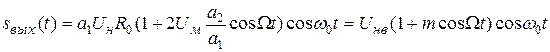
Здесь 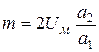
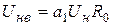
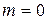
При проектировании передающих систем важным требованием является формирование амплитудно-модулированных колебаний большой мощности при достаточном КПД. Очевидно, что рассмотренный режим работы модулятора не может обеспечить эти требования, особенно первое из них. Поэтому наиболее часто используют так называемый режим больших сигналов.
б. Режим больших входных сигналов
Этот режим устанавливается выбором рабочей точки на ВАХ транзистора, при котором усилитель работает с отсечкой тока. В свою очередь, выбором амплитуды несущего колебания обеспечивается изменение амплитуды импульсов тока коллектора 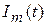
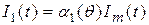
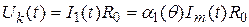
Рис. 8.7. Режим больших входных сигналов амплитудного модулятора
Изменение амплитуды входного высокочастотного напряжения во времени сопровождается изменением угла отсечки, а значит, и коэффициента 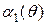
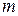
В схеме амплитудного модулятора, приведенной на рис. 8.8, модулирующий сигнал подается на базу транзистора 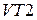
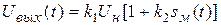
где 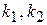
Характеристики амплитудного модулятора
Для выбора режима работы модулятора и оценки качества его работы используют различные характеристики, основными из которых являются: статическая модуляционная характеристика, динамическая модуляционная характеристика и частотная характеристика.
Рис. 8.8. Схема амплитудного модулятора с генератором тока
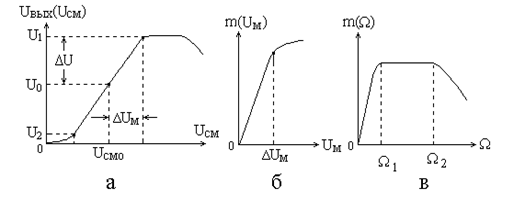
а. Статическая модуляционная характеристика
Статическая модуляционная характеристика (СМХ) – это зависимость амплитуды выходного напряжения модулятора от напряжения смещения при постоянной амплитуде напряжения несущей частоты на входе, т.е. 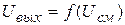
При экспериментальном определении статической модуляционной характеристики на вход модулятора подается только напряжение несущей частоты (модулирующий сигнал не подается), изменяется величина 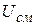
Статическая модуляционная характеристика позволяет определить величину напряжения смещения 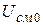
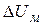
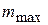
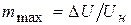
Рис. 8.9. Характеристики амплитудного модулятора
б. Динамическая модуляционная характеристика
Динамическая модуляционная характеристика (ДМХ) – это зависимость коэффициента модуляции от амплитуды модулирующего сигнала, т.е. 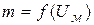
в. Частотная характеристика
Частотная характеристика – это зависимость коэффициента модуляции от частоты модулирующего сигнала, т.е. 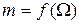
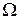
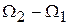
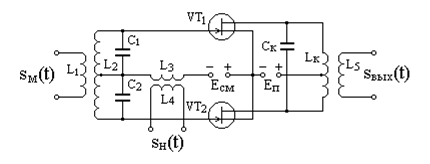
Балансный амплитудный модулятор
Для эффективного использования мощности передатчика применяют балансную амплитудную модуляцию. При этом формируется амплитудно-модулированный сигнал, в спектре которого отсутствует составляющая на несущей частоте.
Схема балансного модулятора (рис. 8.10) представляет собой сочетание двух типовых схем амплитудных модуляторов с определенными соединениями их входов и выходов. Входы по частоте несущего колебания 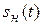
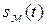
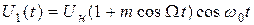
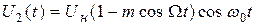
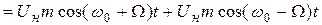
Рис. 8.10. Схема балансного амплитудного модулятора
Таким образом, в спектре выходного сигнала имеются составляющие с частотами