для чего нужен коэффициент дарси
Формула Дарси-Вейсбаха
Формула Дарси-Вейсбаха
Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:
Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
Содержание
Формула Дарси-Вейсбаха
где λ — коэффициент потерь на трение по длине.
Тогда формула Дарси приобретает вид:
или для потери давления:
Последние две зависимости получили название формулы Дарси-Вейсбаха.
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине
Коэффициент λ определяется по разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:
Иногда для гибких труб в расчётах приниают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
где S1 и S2 — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
где S1 и S2 — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
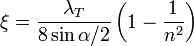
где 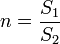
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
См. также
Литература
Полезное
Смотреть что такое «Формула Дарси-Вейсбаха» в других словарях:
Формула Дарси — Формула Вейсбаха[1] в гидравлике эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855… … Википедия
ДАРСИ — ВЕЙСБАХА ФОРМУЛА — (в гидравлике), определяет величину потерь напора на трение при движении жидкости в трубах: hv=(ll/d)(v2/2g), где l коэфф. гидравлич. трения, l и d длина и диаметр трубы, ч ср. скорость течения жидкости, g ускорение свободного падения. Коэфф. l… … Физическая энциклопедия
Формула Шези — Формула Шези формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером гидравликом… … Википедия
Формула Прони — Формула Прони это исторически важная формула в гидравлике, применявшаяся для расчётов потерь напора на трение при течении жидкости по трубам. Это эмпирическая формула, полученная французом Гаспаром де Прони в XIX веке: где hf потери… … Википедия
Дарси, Анри — Анри Дарси Henry Darcy Дата рождения … Википедия
Формула Борда — В гидродинамике, формула (теорема) Борда Карно это эмпирическая формула, описывающая потери энергии (или напора) жидкости, происходящие при местном расширении потока. Эта формула, в отличие от уравнения Бернулли для идеальной жидкости … Википедия
Гидравлические потери — или гидравлическое сопротивление безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2].… … Википедия
Диффузор (гидроаэродинамика) — У этого термина существуют и другие значения, см. Диффузор. Диффузор (в гидроаэродинамике) часть канала (трубы), в которой происходят замедление (расширение) потока. При этом перепад статических давлений на диффузоре может быть меньше, чем… … Википедия
Гидравлический диаметр — Гидравлический диаметр мера эффективности русла в пропускании потока жидкости. Чем меньше гидравлический диаметр, тем большее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока). Определяется по формуле … Википедия
Коэффициент Дарси
Формула Вейсбаха’ [1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году):
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
Содержание
Формула Дарси — Вейсбаха
Тогда формула Вейсбаха приобретает вид:
или для потери давления:
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле Пуазейля:
Иногда для гибких труб в расчётах принимают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
3. При постепенном сужении трубы (конфузор):
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
История
Исторически формула Дарси — Вейсбаха была получена как вариант формулы Прони.
Формула Дарси
Формула Вейсбаха [1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855 году):
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:


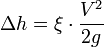
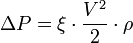
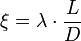
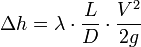
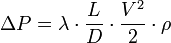
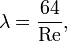
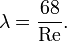
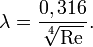

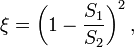

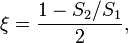




 и диаметром
и диаметром  , то коэффициент Дарси определяется следующим образом:
, то коэффициент Дарси определяется следующим образом:
 — коэффициент потерь на трение по длине.
— коэффициент потерь на трение по длине.


 — число Рейнольдса.
— число Рейнольдса.

 до значений
до значений  . Формула Блазиуса применяется для гидравлически гладких труб.
. Формула Блазиуса применяется для гидравлически гладких труб.

 .
.
 и
и  — площади поперечного сечения трубы, соответственно перед расширением и после него.
— площади поперечного сечения трубы, соответственно перед расширением и после него.

 ,
, — степень сужения;
— степень сужения;  — коэффициент потерь на трение по длине при турбулентном режиме.
— коэффициент потерь на трение по длине при турбулентном режиме.


