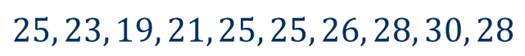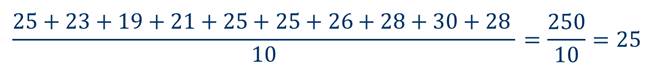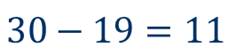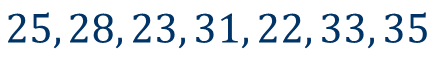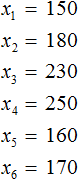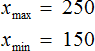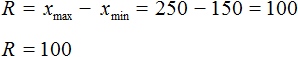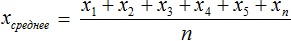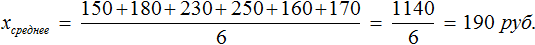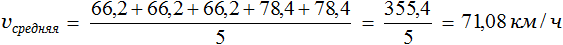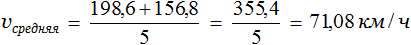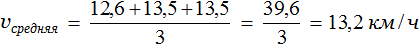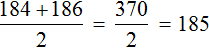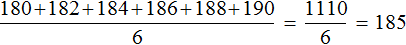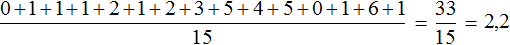для чего нужен размах ряда
Вариация, размах, межквартильный размах, среднее линейное отклонение
В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.
В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.
Среднее арифметическое, размах и мода
Урок 10. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Среднее арифметическое, размах и мода»
· ввести понятие «среднее арифметическое числового ряда»;
· ввести понятия «размах ряда», «мода ряда»;
· разобрать, где находят применение рассмотренные статические характеристики.
Давайте рассмотрим пример.
Ежедневно в течение 10 дней в полдень измеряли температуру воздуха (в градусах Цельсия) и получили следующие данные.
Пользуясь этим рядом, мы можем определить среднюю температуру воздуха, наблюдаемую в течение этих десяти дней.
Число 25 называют средним арифметическим рассматриваемого ряда чисел.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Таким образом, умея находить среднее арифметическое ряда чисел, мы можем найти средний расход холодной воды семьёй в течение года
средний балл ученика за четверть
среднюю урожайность пшеницы за последние 5 лет и так далее.
Вернёмся к нашему примеру. Обратите внимание, что температура воздуха в некоторые дни существенно отличается от 25 градусов Цельсия (то есть от средней температуры). Так, самая высокая температура равна 30 градусам, а самая низкая – 19 градусам.
Найдём разность между наибольшим и наименьшим значениями:
Говорят, что размах ряда равен 11.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда находят, когда хотят узнать, насколько велик разброс данных в ряду. Так, например, в нашем примере размах ряда показывает колебание температуры воздуха в течение 10 дней.
Но кроме среднего арифметического и размаха ряда данных, нас может заинтересовать вопрос: какая температура воздуха чаще всего устанавливалась за 10 дней? Заметим, что чаще всего в нашем ряду встречается число 25. Это число называют модой рассматриваемого ряда.
Модой ряда называется число, которое встречается в данном ряду чаще других.
Стоит отметить, что ряд может иметь более одной моды.
Также ряд может и не иметь моды.
Моду ряда находят, когда хотят выяснить некоторый характерный показатель. Например, удобно воспользоваться этим показателем при изучении спроса покупателей на мужскую обувь, чтобы определить какой размер самый популярный.
Рассмотрим ещё один пример.
Посмотрите, среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда, а вот мода всегда совпадает хотя бы с одним из чисел. Причем, если среднее арифметическое мы можем найти только для числового ряда, то понятие «мода» относится не только к числовым рядам.
Например, проведя опрос группы людей, можно определить, какой из видов спорта более популярен. И модой будут служить те ответы, которые чаще всего встречаются.
Рассмотренные на уроке характеристики (среднее арифметическое, размах и мода) применяются в статистике.
Статистика (от латинского слова статус, что означает состояние, положение вещей) – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в обществе и природе.
Основываясь на примерах, которые мы с вами рассматривали на уроке, можно сказать, что статистика используется в различных сферах деятельности человека.
Для чего нужен размах ряда
В этом учебном году мы начали изучать два предмета: алгебру и геометрию. При изучении алгебры что-то мне знакомо из курса 5,6 классов, что-то мы изучаем более основательно и углубленно, многое узнаем нового. Вот новое для меня при изучении алгебры – это знакомство с некоторыми статистическими характеристиками: размах и мода. Со средним арифметическим мы встречались уже ранее. Еще интересным оказалось, что эти характеристики применяются не только на уроках математики, но и в жизни, на практике (в производстве, в сельском хозяйстве, в спорте и т.д.).
Когда мы в классе на уроке решали задачи к этому пункту, то возникла идея составить самим задачи и подготовить к ним презентации, то есть как бы начать создавать свой задачник. Каждый придумывает задачу, делает к ней презентацию, как бы каждый работает над своим мини-проектом, а на уроке все вместе решаем, обсуждаем. Если допущены ошибки, то их исправляем. А в конце провести публичную защиту этих мини-проектов.
Цель моей работы: изучение статистики.
Задачи: начать разработку задачника по статистике в виде компьютерных презентаций.
Предмет исследования: статистика.
Объект исследования: статистические характеристики (среднее арифметическое, размах, мода).
В ходе изучения раздела «Статистические характеристики» мы познакомились с такими понятиями: среднее арифметическое, размах, мода. Эти характеристики находят применение в статистике. Эта наука изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т.п.
“Статистика знает всё”, – утверждали Ильф и Петров в своем знаменитом романе “Двенадцать стульев” и продолжали: “Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц. ” Это ироническое описание дает довольно точное представление о статистике (от лат. status – состояние) – науке, изучающей, обрабатывающей и анализирующей количественные данные о самых разнообразных массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления.
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
А еще есть статистика финансовая, налоговая, биологическая, метеорологическая. [1]
В школьном курсе алгебры мы рассматриваем понятия и методы описательной статистики, которая занимается первичной обработкой информации и вычислением наиболее показательных числовых характеристик. По словам английского статистика Р. Фишера: “Статистика может быть охарактеризована как наука о сокращении и анализе материала, полученного в наблюдениях”. Всю совокупность числовых данных, полученных в выборке можно (условно) заменить несколькими числовыми параметрами, некоторые из них мы уже рассматривали на уроках – это среднее арифметическое, размах, мода. Результаты статистических исследований широко используются для практических и научных выводов, поэтому важно уметь определять эти статистические характеристики.
Результаты статистических исследований широко используются для практических и научных выводов. [2]
Определение 1. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. [3]
Пример: При изучении учебной нагрузки выделили группу из 12 учащихся 7 класса. Просили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и полученную сумму разделить
Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.
Среднее арифметическое является важной характеристикой ряда чисел но иногда полезно рассматривать и другие средние.
Определение 2. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. [4]
Пример: При анализе сведений о времени, затраченном учащимися на выполнение домашнего задания по алгебре, нас могут заинтересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Например, интересно знать, какой расход времени является типичным для выделенной группы учащихся, т.е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что в нашем примере это число 25. говорят, что число 25 – мода рассматриваемого ряда.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Например, в ряду чисел 47, 46, 50, 47, 52, 49, 45, 43, 54, 52, 47, 52 две моды – это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа – менее трех раз.
В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.
Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Мода—показатель, который широко используется в статистике. Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода — наиболее часто встречающийся заказ.
Однако нахождение среднего арифметического или моды далеко не всегда позволяет делать надежные выводы на основе статистических данных. если у нас есть ряд данных, то для обоснованных выводов и надежных прогнозов на их основе, помимо средних значений, надо еще указать, насколько используемые данные различаются между собой. Одним из статистических показателей различия или разброса данных является размах.
Определение 3. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. [5]
Пример: В рассмотренном выше примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 минут. Однако анализ проведенного ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 минут, т.е. от среднего арифметического. Наибольший расход равен 37 минут, а наименьший – 18 минут. Разность между наибольшим и наименьшим расходом времени составляет 19 минут. Вот в этом случае рассматривается еще одна статистическая характеристика – размах. Размах ряда находят, когда хотят определить, как велик разброс данных в ряду.
А теперь хочу представить результаты нашей работы: мини-проекты для создания задачника по статистике.
Задача № 1. Автор Кушнарев Павел, учащийся 7 класса.
Я работаю в салоне-магазине «Супер-авто» главным менеджером отдела продаж. Наш салон предоставлял автомобили для участия в игре «полный привод». В прошлом году на выставке-продаже наши машины имели успех! Результаты продаж следующие:
Элементы статистики
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
Элементы выборки обозначаются с помощью переменных с индексами 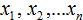
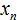
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
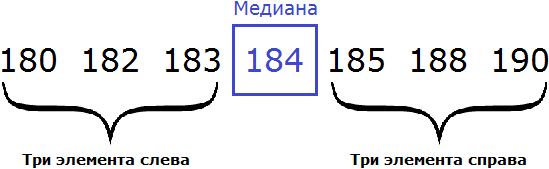
Выпишем рост спортсменов отдельно:
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
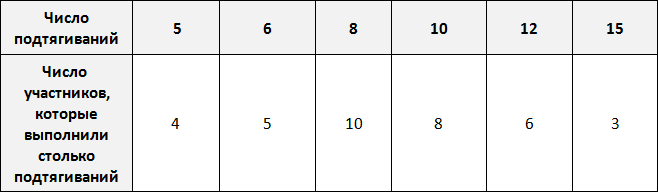
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
42 thoughts on “Элементы статистики”
Спасибо, что вы вернулись.
Будут ли новые уроки?