для чего нужна парабола

Презентация на тему: «Парабола в жизни».

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Так ли уж редко мы встречаемся с параболой? Судьба, как ракета, летит по параболе…

Зачем мы учили это? Параболой называется график функции у=х², точка О(0;0) – вершина параболы, ось ОY – ось параболы, равенство у=х² – уравнение параболы y x O

Мы посмотрели вокруг и увидели

Начнём с простого. Камень, брошенный вверх летит по параболе. Видео по ссылке:http://files.school-collection.edu.ru/dlrstore/2e7210fb-017a-4d37-b413-5895ed1baec2/a01.swf

Параболическая антенна Можно увидеть около любого аэродрома. Используется для того, чтобы собрать в одну точку сигналы радиолокатора, отраженные от самолета.

В прожекторах Свет, исходящий из фокуса параболического зеркала, после отражения образует параллельный пучок и не рассеивается. Поэтому автомобильные фары имеют форму параболоида.

Парабола в архитектуре

Парабола и Космос Если телу придать начальную скорость в пределах от 7,9 км в с до11,2 км в с, то оно на Землю не упадет, а превратится в ее спутник, движущийся по эллипсу.При скорости же 11,2 км в с тело вновь начнет двигаться по параболе и уйдет от Земли навсегда. Итак, космические корабли выходят на орбиту по параболе!

Парабола и архитектра Форма параболы иногда используется в архитектуре для строительства крыш и куполов

«Параболы»—аппараты с параболической формой крыла в плане. Б. И. Черановский предложил проект самолета типа летающего крыла с удлинением, очерченного по параболе

Параболические траектории струй воды

Есть парабола и в телескопах Телескоп Ньютона. Этот инструмент самый популярный у любителей вследствие легкости его изготовления (небольшой цены) и возможности применения, как для визуальных, так и для фотографических наблюдений. Главное зеркало обычно имеет форму параболы. Параболическое зеркало

Переводим природу в математику.

Пример1 Количество тепла, выделяемого за 1 с при прохождении тока в проводнике с постоянным сопротивлением R Ом и силой тока I ампер, выражается квадратичной функцией Q=0,24R2 (калорий). Графиком этой функции является правая ветвь параболы с вершиной в начале координат.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-240390

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Утверждены сроки заключительного этапа ВОШ

Время чтения: 1 минута

Утверждено стратегическое направление цифровой трансформации образования

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Россияне чаще американцев читают детям страшные и печальные книжки

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Парабола

Парабола, её фокус и директриса
Коническое сечение:
Эксцентриситет:
Уравнение:
гипербола · парабола · эллипс · окружность

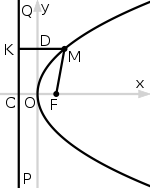
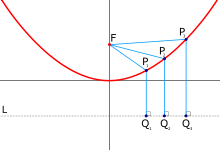
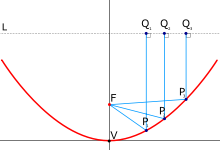
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Содержание

Уравнения

0″ border=»0″ /> (или , если поменять местами оси).

Уравнение директрисы : , фокус — , таким образом начало координат — середина отрезка . По определению параболы для любой точки , лежащей на ней выполняется равенство . и , тогда равенство приобретает вид:

.

После возведения в квадрат и некоторых преобразований получается равносильное уравнение .

Квадратное уравнение при также представляет собой параболу и графически изображается той же параболой, что и , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке , координаты которой вычисляются по формулам:

где — дискриминант

Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a Расчёт коэффициентов квадратного уравнения

Если для уравнения известны координаты 3-х различных точек его графика , , , то его коэффициенты могут быть найдены так:

Свойства

Связанные определения

Параболы в физическом пространстве

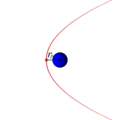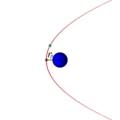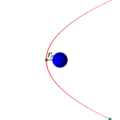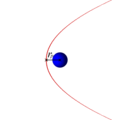
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы (или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности аппаратов Вояджер).

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

Параболическая орбита и движение спутника по ней (анимация)

Параболические траектории струй воды

Вращающийся сосуд с жидкостью

См. также

Примечания

Литература

Ссылки

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Конические сечения
Главные типы	Эллипс • Гипербола • Парабола
Вырожденные	Точка • Прямая • Пара прямых
Частный случай эллипса	Окружность
Геометрическое построение	Коническое сечение • Шары Данделена
См. также	Коническая константа
Математика • Геометрия

Полезное

Смотреть что такое «Парабола» в других словарях:

ПАРАБОЛА — (греч. parabole, от parabollo сближаю). 1) иносказание, притча. 2) кривая линия, происходящая от сечения конуса плоскостью, параллельною какой нибудь его производящей. 3) кривая линия, образующаяся при полете бомбы, ядра и т. п. Словарь… … Словарь иностранных слов русского языка

парабола — иносказание, притча (Даль) См. пример … Словарь синонимов

ПАРАБОЛА — (греч. parabole) плоская кривая (2 го порядка). Парабола множество точек М, расстояния которых до данной точки F (фокуса) и до данной прямой D1D2 (директрисы) равны. В надлежащей системе координат уравнение параболы имеет вид: y2=2px, где р=2OF.… … Большой Энциклопедический словарь

ПАРАБОЛА — ПАРАБОЛА, математическая кривая, КОНИЧЕСКОЕ СЕЧЕНИЕ, образуемое точкой, двигающейся таким образом, что ее расстояние до неподвижной точки, фокуса, равно ее расстоянию до неподвижной прямой, директрисы. Парабола образуется при разрезе конуса… … Научно-технический энциклопедический словарь

ПАРАБОЛА — жен., греч. иносказанье, притча. | мат. кривая черта, из числа конических сечений; разрез сахарной головы накось, опостен (параллельно) противной стороне. Парабольные вычисленья. Параболическое реченье, инословие, иноречие, переносное.… … Толковый словарь Даля

ПАРАБОЛА — (1) незамкнутая кривая линия 2 го порядка на плоскости, являющаяся графиком функции у2 = 2рх, где р параметр. Параболу получают при пересечении кругового (см.) плоскостью, не проходящей через его вершину и параллельной одной из его образующих.… … Большая политехническая энциклопедия

ПАРАБОЛА — (от греческого parabole), плоская кривая, расстояния любой точки M которой до данной точки F (фокуса) и до данной прямой D 1D1 (директрисы) равны (MD=MF) … Современная энциклопедия

ПАРАБОЛА — ПАРАБОЛА, параболы, жен. (греч. parabole). 1. Кривая второго порядка, представляющая коническое сечение прямого кругового конуса плоскостью, параллельною одной из образующих (мат.). || Путь, описываемый тяжелым телом (напр. пулей), брошенным под… … Толковый словарь Ушакова

ПАРАБОЛА — ПАРАБОЛА, ы, жен. В математике: состоящая из одной ветви незамкнутая кривая, образующаяся при пересечении конической поверхности плоскостью. | прил. параболический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ПАРАБОЛА — «ПАРАБОЛА», Россия, 1992, цв., 30 мин. Документальное эссе. Попытка понять мистическую суть сказаний удмуртов маленького народа в Поволжье. Режиссер: Светлана Стасенко (см. СТАСЕНКО Светлана). Автор сценария: Светлана Стасенко (см. СТАСЕНКО… … Энциклопедия кино

Источник

Квадратичная функция. Построение параболы

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

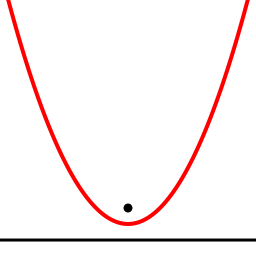
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Рассмотрим три случая:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Как строим:

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Как строим:

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Источник

Параболы в окружающем мире.

Квадратичная функция

Автор работы: Султашева Алина

Кашкарбаевна, 8 класс,

Руководитель:

Базарбаева Зайра Хайргельдыновна,

учитель математики и информатики

I. Уникальное свойство параболы.

1.1.Парабола в древности и до наших дней.

1.2.Практическое применение параболы.

1.3.Параболы в окружающем мире.

II. Изучение квадратичной функции.

2.2.Понятие квадратичной функции и ее свойства.

III. Исследование квадратичной функции.

3.1.Зависимость графика параболы от коэффициентов.

3.2.Алгоритм построения графика функции у=а(х+m)2 + n.

«Что чувство удивления – могучий источник желания знать:

от удивления к знаниям – один шаг».

Введение

В 8 классе на уроке алгебры мы впервые встретились с квадратичной функцией. Я считаю, что рассмотреть свойства этой функции и понять их с помощью графика легче.

Если рассмотреть, как абстрактные математические понятия встречаются в действительности, то предмет математики становится интересней, а наши знания более осмысленными и глубокими.

В настоящее время очень популярны нестандартные задачи, нестандартные решения и применения; я считаю, что квадратичная функция и парабола относится к разряду таких применений; поэтому выбранная мной тема актуальна.

Цель исследования: изучение некоторых свойств квадратичной функции и особенностей ее графика.

Задачи исследования:

1. Изучить роль математики в развитии цивилизации и культуры.

2. Ознакомиться с оптическими свойствами параболы, рассмотреть их применение в технике, быту.

3. Изучить некоторые свойства квадратичной функции.

4. Исследовать квадратичную функцию и составить алгоритм построения графика квадратичной функции, основываясь на её свойствах.

Объект исследования: квадратичная функция и парабола.

Предмет исследования: влияние разных коэффициентов на внешнюю форму параболы.

В своей работе я использовала следующие методы:

1) сбор и анализ литературы по теме;

4) работа с помощью программы Microsoft Office Excel.

Основными этапами исследования были:

· овладение методикой построение графиков с помощью программы Microsoft Office Excel,

· проведение опытов по построению квадратичной функции и параболы,

· обобщение полученных данных и разработка алгоритма построения графика квадратичной функции.

I. Уникальное свойство параболы.

Парабола в древности и до наших дней.

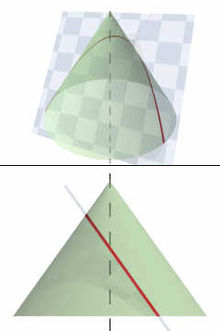
Согласно легенде, в 212 году до н.э., Архимед из Сиракуз сжёг флот римлян, обороняя свой город с помощью параболических зеркал. Этот день уцелевшим римлянам запомнился на всю жизнь. Почти полтысячи маленьких солнц вдруг загорелись на крепостной стене. Сначала они просто ослепляли, но через некоторое время произошло нечто фантастическое: передовые римские корабли, подошедшие к Сиракузам, один за другим вдруг начали вспыхивать, как факелы. Бегство римлян было паническим. Так для защиты своего города Архимед использовал оптическое свойство параболы (Приложение 1, рис.1).

Аполлоний Пергский (Перге, 262 до н.э. — 190 до н.э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н.э., он прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата (Приложение 1, рис. 2, 3).

Практическое применение параболы.

В технике.

Параболоид обладает следующим свойством:

· Все лучи, исходящие из особой точки – фокуса параболы (находящегося на оси z), после отражения от «стенок» параболоида образуют лучи, параллельные оси z.

· Все лучи, параллельные оси z, после отражения от параболоида собираются в одной точке – фокусе параболоида. На этом свойстве основано конструирование автомобильных фар, прожекторов, параболических антенн и других устройств с отражающими поверхностями, имеющими формы параболоидов (Приложение 2, рис.1).

Лучи от далеких звезд приходят к нам в виде пучка параллельных лучей, двигающихся вдоль оси параболы, и отражаясь собираются в его фокусе. Если поместить туда фотопластинку, то получаем возможность усилить световой поток, идущий от звезды. На этом основана идея телескопов, антенн, локаторов, зеркала которых выполнены в виде параболоидов вращения.

В нашей стране существуют прожекторные полки, предназначенные для обеспечения боевых действий частей истребительной авиации зоны ПВО. В 1932 году в Москве формируется первый территориальный прожекторный полк. Такой полк охранял воздушные рубежи над Москвой в первые дни войны, создавая световые поля в которые то и дело врывались вражеские самолеты. На подступах к Москве самолеты противника были встречены нашими ночными истребителями и организованным огнем зенитной артиллерии. В результате этого было сбито более 200 самолетов противника. (Приложение 2, рис. 2).

Идя в ногу со временем, многие меняют телевизионную антенну. После того, как устанавливается новая параболическая, то убеждаются в том, что идет расширение диапазона, улучшение качества изображения, дальность приема передач. Эти изменения связаны с формой антенны (Приложение 2,рис.4). Параболическую антенну называют зеркальной, т.к. она состоит из основного параболического зеркала и облучателя. Электромагнитная энергия подводится к облучателю, устанавливаемому у вершины параболоида, и излучается на малое зеркало, после отражения, от которого направляется на основное зеркало. (Приложение 2, рис.5).

В космосе.

Некоторые космические тела, такие как кометы или астероиды, проходящие вблизи крупных космических объектов на высокой скорости, имеют траекторию движения в форме параболы. Скорость примерно равна 11,2 км/с и называется параболической или космической скоростью. Масса таких тел мала, а скорость велика. Поэтому они не захватываются гравитационным полем планет (звезд) и продолжают свободный полет. Это свойство малых космических тел используется при гравитационных маневрах космических кораблей.

А для тренировок будущих космонавтов, на земле проводятся специальные полеты самолетов по траектории параболы, чем достигается эффект невесомости в гравитационном поле земли (Приложение 2,рис.6,7).

В медицине.

В медицине используется параболическое устройство, за счет которого удается разрушить камень в почках. Человека помещают на кресло, и подают электричество на параболическое устройство. Все лучи концентрируются в одной точке (фокус), фокус рассчитан на особое местонахождение (заранее). В данном случае это будет сам камень в почке (Приложение 2, рис.8).

Параболы в окружающем мире.

В природе.

Когда мы прикладываем руку к уху, чтобы лучше слышать, мы неосознанно формируем параболу в трех измерениях (Приложение 3, рис.1, 2).

В архитектуре.

Параболические формы можно встретить в архитектурных сооружениях.

-Использование математического знания о геометрии конических сечений наблюдается с древнейших времен. Вполне вероятно, что строители в прошлом пользовались в этой области знания интуитивно (Приложение 3, рис.3).

-Золотые ворота — один из немногих памятников оборонного зодчества Киевской Руси периода правления Ярослава Мудрого (Приложение 3, рис.4).

-Мост Золотые Ворота — висячий мост через пролив Золотые Ворота. Он соединяет город Сан-Франциско на севере полуострова Сан-Франциско и южную часть округа Марин, рядом с пригородом Саусалито. Мост Золотые Ворота был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года (Приложение 3, рис.5).

— Благодаря своей отражающей способности параболы используют в постройке куполов дворцов и соборов, а также амфитеатров, чтобы зрители четко слышали актеров. (Приложение 3, рис.6).

-Архитектурные свойства арки в форме параболы делают ее идеальной математически. Перевернутая цепная линия – это арка, которая держит сама себя и не требует никаких дополнительных опор. Ворота Сент-Луиса в Миссури – прекрасный пример такой арки (Приложение 3, рис.7).

-Знаменитый испанский архитектор Гауди обожал эту кривую и использовал во многих своих творениях, например, в Каса Мила в Барселоне (Приложение 3, рис.8).

— Стадион Фишт. На нем будет открытие и закрытие Олимпиады. А так же игры Чемпионата мира по футболу 2018г. (Приложение 3, рис.11).

Источник