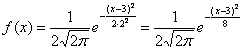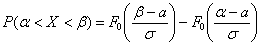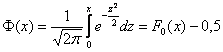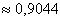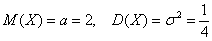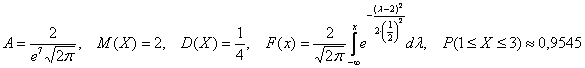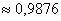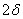для чего нужно нормальное распределение
Нормальное распределение
Материал из MachineLearning.
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Содержание
Моделирование нормальных случайных величин
Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.
Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.
Свойства
Статистическая проверка принадлежности нормальному распределению
Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:
Многомерное нормальное распределение
Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения.
Случайный вектор имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
Замечания
Свойства многомерного нормального распределения
См. также
Заключение
Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:
Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.
Нормальное распределение (Normal Distribution)
Нормальное распределение (распределением Гаусса или Гаусса — Лапласа) – распространенная разновидность непрерывного распределения вероятностей для случайной величины.
Помните колоколообразную кривую? Вот эту:
Долгое время она служила главным критерием профессиональной оценки сотрудников американских учреждений, и равнодушных не оставляла, ведь от нее зависело, как себя позиционирует человек и его начальство.
Нормальное распределение – это ключевая концепция Статистики (Statistics) и основа Науки о данных (Data Science). При выполнении Разведочного анализа данных (EDA) мы сначала стремимся найти их распределение вероятностей, и наиболее распространенный ее вид – нормальное распределение.
Посмотрите на распределение вероятностей окупить инвестиции в фондовый индекс S&P 500:
Да-да, вероятность «выйти в ноль» выше остальных! Также справедливо утверждение, что вероятность потерять больше как бы тает вместе с отрицательным процентом возврата. Белой непрерывной линией обозначено предсказание кривой нормального распределения. Прочие наблюдения, такие как вес при рождении и показатель IQ, часто следуют нормальному распределению подобным образом.
Еще одна причина, по которой нормальное распределение становится важным для Дата-сайентистов (Data Scientist) – это Центральная предельная теорема (Central Limit Theorem). Эта теорема объясняет магию математики и является основой методов проверки гипотез.
В этой статье мы поймем важность и различные свойства нормального распределения, а изучим, как использовать эти свойства для проверки нормальности наших данных.
Свойства нормального распределения
Кривая стандартного нормального распределения симметрична относительно Среднего арифметического (Mean), Медианы (Median) и Моды (Mode). Более того, также являются нормальным распределением произведение двух нормальных распределений и их сумма. Магия, не правда ли? Существуют и другие, более сложные закономерности, пока обойдемся самыми понятными.
Эмпирическое правило
Вы слышали об эмпирическом правиле? Оно часто используется в статистике и гласит: «68,27% наблюдений случайной Выборки (Sample) лежат в пределах одного Стандартного отклонения (Standard Deviation), 95,45% – в пределах двух, а 99,73 – в пределах трех стандартных отклонений от среднего»:
Это правило позволяет нам идентифицировать Выбросы (Outlier) и очень полезно при Проверке на нормальность (Normality Test).
Стандартное нормальное распределение
Стандартное нормальное распределение – это частный случай нормального распределения, когда среднее значение равно нулю и стандартное отклонение равно единице. Любое нормальное распределение мы можем преобразовать его в стандартное, используя формулу:
Пример. Есть два интерна: Левин и Ричардс. Левин набрал 65 баллов на экзамене по терапии, а Ричардс – 80 баллов на экзамене по кожной венерологии. Верно ли, что Ричардс учился лучше, чем Левин?
Нет, потому что манера поведения людей в терапии отличается от того, как люди проявляют себя в кожной венерологии. Таким образом, прямое сравнение простым сравнением оценок некорректно.
Теперь предположим, что отметки теста по терапии подчиняются нормальному распределению со средним значением 60 и стандартным отклонением 4. С другой стороны, отметки о кожвенерологии подчиняются нормальному распределению со средним значением 79 и стандартным отклонением 2.
Нам нужно будет вычислить Стандартизированную оценку (Z-score) путем стандартизации обоих этих распределений:
Таким образом, Левин набрал 1,25 стандартного отклонения выше среднего, в то время как Ричардс – только 0,5. Следовательно, Левин показал себя лучше:
Асимметричное распределение
Нормальное распределение – это симметрично, что означает, что его «хвосты» слева и справа – зеркальные отображения друг друга. Но это не относится к большинству реальных наборов данных. Как правило, мы будем иметь дело со скошенными асимметричными распределениями.
Визуальная оценка нормальности
Для таких целей принято использовать три вида графиков:
Для оценки нормальности распределения также используют Скошенность (Skewness) и Эксцесс (Kurtosis).
Нормальное распределение и Python
Посмотрим, как выглядит код, визуализирующий распределение и заодно рассчитывающий основные метрики Датасета (Dataset). Для начала импортируем необходимые библиотеки:
Определим функцию, которая пройдется по всем столбцам датасета, рассчитает основные статистические метрики (среднее, минимум, максимум и т.д.):
Построим тройной график:
Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Нормальное распределение (Гаусса) в Excel
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
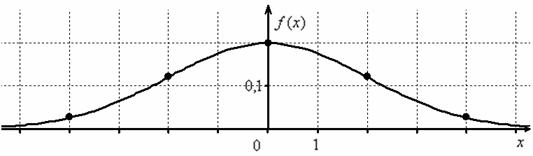
Кривая нормального распределения Гаусса имеет следующий вид.
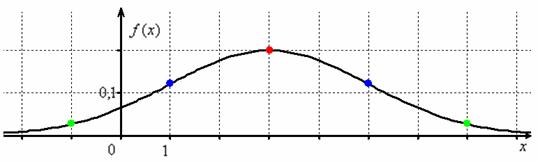
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
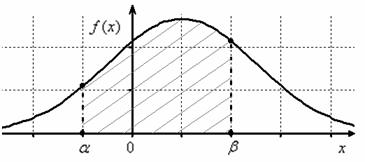
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z
Нормальный закон распределения вероятностей
Без преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто сталкиваемся с тем, что чего-то бывает мало, и что бывает норма: 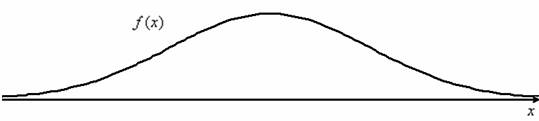
Перед вами принципиальный вид функции плотности нормального распределения вероятностей, и я приветствую вас на этом интереснейшем уроке.
Какие можно привести примеры? Их просто тьма. Это, например, рост, вес людей (и не только), их физическая сила, умственные способности и т.д. Существует «основная масса» (по тому или иному признаку) и существуют отклонения в обе стороны.
Это различные характеристики неодушевленных объектов (те же размеры, вес). Это случайная продолжительность процессов, например, время забега стометровки или превращения смолы в янтарь. Из физики вспомнились молекулы воздуха: среди них есть медленные, есть быстрые, но большинство двигаются со «стандартными» скоростями.
Более того, даже дискретные распределения бывают близкИ к нормальному, и в конце урока мы раскроем важный секрет «нормальности». Но прежде, математика, математика, математика, которая в древности не зря считалась философией!
Непрерывная случайная величина 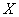
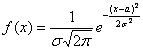
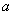
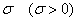
Данная функция получила фамилию некоронованного короля математики, и я не могу удержаться, чтобы не запостить: 
Одну из таких купюр мне довелось лично держать в руках, и ещё будучи школьником я внимательно изучил функцию Гаусса. Педантичные немцы отобразили все её особенности (на картинке видно плохо), и мы с толком, с расстановкой приступаем к их немцев изучению.
Начнём с того, что для функции 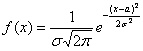
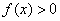
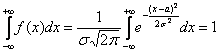
Любопытно отметить, что сам по себе неопределённый интеграл 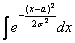
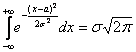
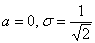
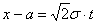
Следующие замечательные факты я тоже приведу без доказательства:
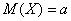
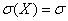
Эти значения выводятся с помощью общих формул математического ожидания и дисперсии, и желающие / нуждающиеся могут ознакомиться с подробными выкладками в учебной литературе, и совсем здОрово, если вам удастся провести их самостоятельно.
Ну а мы переходим к насущным практическим вопросам. Практики сегодня будет много, и она будет интересна не только «чайникам», но и более подготовленным читателям:
Нормально распределённая случайная величина задана параметрами 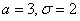
Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.
Первый момент касается обозначений. Они стандартные, и никаких вольностей: математическое ожидание обозначают буквой 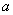
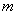
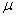
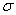
Решение начнём шаблонной фразой: функция плотности нормально распределённой случайной величины имеет вид 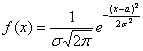
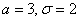
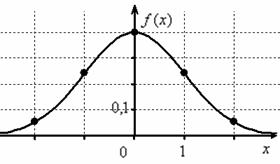
Первая, более лёгкая часть задачи выполнена. Теперь график. Вот на нём-то, на моей памяти, студентов «заворачивали» десятки раз, причём, многих неоднократно. По той причине, что график 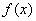
Сначала полная картина, затем комментарии:
Строим декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:
по оси абсцисс: 2 тетрадные клетки = 1 ед.;
по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке 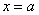
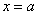
И логично, что в первую очередь удобно найти максимум функции. В данном примере он находится в точке 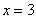
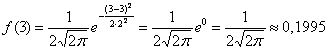
Отмечаем вершину графика (красная точка).
Далее вычислим значения функции при 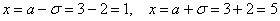

Отмечаем синим цветом.
Внимание! 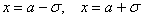
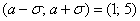
Далее отклоняемся от центра ещё на одно стандартное отклонение 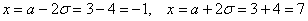
Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.
На завершающем этапе аккуратно чертим график, и особо аккуратно отражаем его выпуклость / вогнутость! Ну и, наверное, вы давно поняли, что ось абсцисс – это горизонтальная асимптота, и «залезать» за неё категорически нельзя!
При электронном оформлении решения график легко построить в Экселе, и неожиданно для самого себя я даже записал короткий видеоролик на эту тему. Но сначала поговорим о том, как меняется форма нормальной кривой в зависимости от значений 
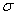
При увеличении или уменьшении «а» (при неизменном «сигма») график сохраняет свою форму и перемещается вправо / влево соответственно. Так, например, при 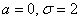
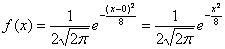
Нормально распределённая величина с нулевым математическим ожиданием получила вполне естественное название – центрированная; её функция плотности 
В случае изменения «сигмы» (при постоянном «а»), график «остаётся на месте», но меняет форму. При увеличении 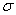
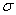
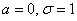
Всё в полном соответствии с геометрическими преобразованиями графиков.
Нормальное распределёние с единичным значением «сигма» называется нормированным, а если оно ещё и центрировано (наш случай), то такое распределение называют стандартным. Оно имеет ещё более простую функцию плотности, которая уже встречалась в локальной теореме Лапласа: 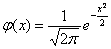
Ну а теперь смотрим кино:
Да, совершенно верно – как-то незаслуженно у нас осталась в тени функция распределения вероятностей. Вспоминаем её определение:
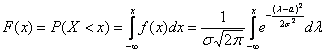
Внутри интеграла обычно используют другую букву, чтобы не возникало «накладок» с обозначениями, ибо здесь каждому значению 
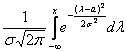
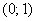
Почти все значения 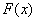
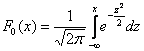
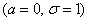
Раз, два – и готово:
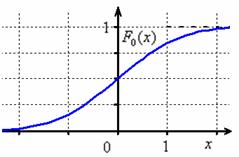
На чертеже хорошо видно выполнение всех свойств функции распределения, и из технических нюансов здесь следует обратить внимание на горизонтальные асимптоты и точку перегиба 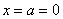
Теперь вспомним одну из ключевых задач темы, а именно выясним, как найти 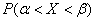
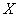
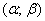
но каждый раз вымучивать приближенное значение 
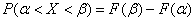
! Вспоминаем также, что
Тут можно снова задействовать Эксель, но есть пара весомых «но»: во-первых, он не всегда под рукой, а во-вторых, «готовые» значения 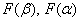
Об этом я неоднократно рассказывал ранее: в своё время (и ещё не очень давно) роскошью был обычный калькулятор, и в учебной литературе до сих пор сохранился «ручной» способ решения рассматриваемой задачи. Его суть состоит в том, чтобы стандартизировать значения «альфа» и «бета», то есть свести решение к стандартному распределению:
Примечание: функцию 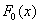
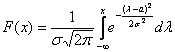
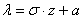
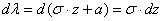
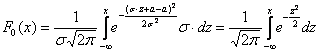
и из проведённой замены как раз следует формула 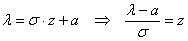
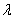
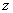
Зачем это нужно? Дело в том, что значения 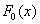
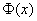
В силу очевидной нечётности функции Лапласа (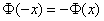
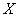
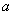
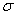
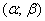
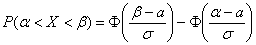
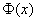
Таким образом, наша задача становится чуть ли не устной! Порой, здесь хмыкают и говорят, что метод устарел. Может быть…, но парадокс состоит в том, что «устаревший метод» очень быстро приводит к результату! И ещё в этом заключена большая мудрость – если вдруг пропадёт электричество или восстанут машины, то у человечества останется возможность заглянуть в бумажные таблицы и спасти мир =)
Из пункта 
Решение: в задаче рассматривается нормально распределённая случайная величина 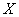
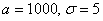
Если в нашем распоряжении есть таблица значений функции 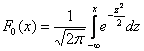
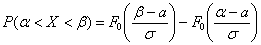
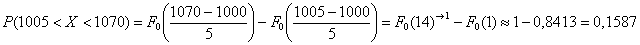
Для самопроверки можно задействовать экселевскую функцию =НОРМСТРАСП(z) или напрямую «забить» 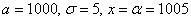
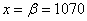
Если же в нашем распоряжении есть таблица значений функции Лапласа 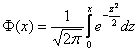
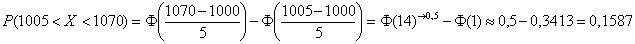
Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.
Напоминаю, что 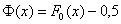
Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:
– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов
Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.
В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.
И уже в этом примере нам встретился особый случай – когда интервал 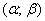
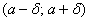
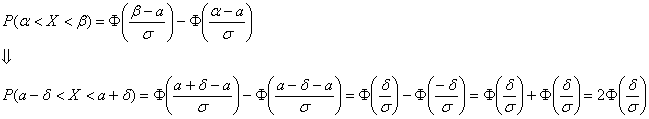
Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство можно «упаковывать» с помощью модуля:
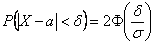
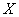
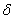
Хорошо то решение, которое умещается в одну строчку:)
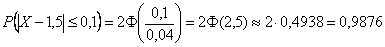
Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На поставленный вопрос отвечает так называемое
правило «трех сигм»
Его суть состоит в том, что практически достоверным является тот факт, что нормально распределённая случайная величина 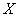
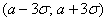
И в самом деле, вероятность отклонения от матожидания менее чем на 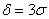
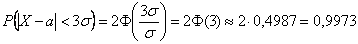
В «пересчёте на подшипники» – это 9973 штуки с диаметром от 1,38 до 1,62 см и всего лишь 27 «некондиционных» экземпляров.
В практических исследованиях правило «трёх сигм» обычно применяют в обратном направлении: если статистически установлено, что почти все значения исследуемой случайной величины укладываются в интервал длиной 6 стандартных отклонений, то появляются веские основания полагать, что эта величина распределена по нормальному закону. Проверка осуществляется с помощью теории статистических гипотез.
Продолжаем решать суровые советские задачи:
Случайная величина 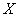
Решение очень простое. По условию, 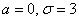
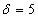
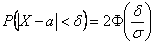
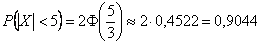
Ответ:
Прорешанная задача принципиально отличается от вроде бы похожего Примера 3 урока о равномерном распределении. Там была погрешность округления результатов измерений, здесь же речь идёт о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине экспериментатора – когда мы, например, «на глазок» снимаем показания со стрелки тех же весов.
Помимо прочих, существуют ещё так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно «прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически ведь можно обсчитать. Однако, в любом случае, случайной такая ошибка не будет, и её матожидание отлично от нуля.
…срочно разрабатываю курс по подготовке продавцов =)
Самостоятельно решаем обратную задачу:
Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно 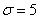
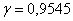
Пункт 5* расчётного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.
И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:
Нормально распределенная случайная величина 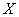
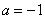
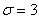
а) записать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что 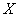
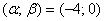
в) найти вероятность того, что 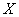
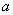
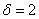
г) применяя правило «трех сигм», найти значения случайной величины 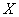
Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц 😉
Ну а я разберу пример повышенной сложности:
Плотность распределения вероятностей случайной величины 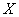
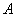
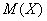
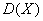
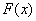
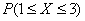
Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по себе присутствие экспоненты ещё ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения ещё нужно обосновать:
Так как функция 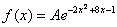
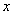
Приводим. Для этого выделяем полный квадрат и организуем трёхэтажную дробь: 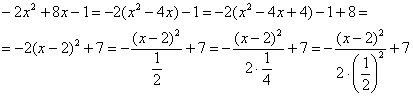
Обязательно выполняем проверку, возвращая показатель в исходный вид: 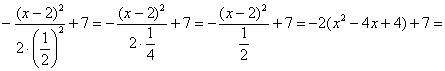
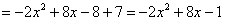
Таким образом:
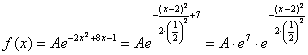
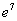
Теперь найдём значение параметра 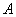
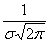
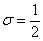
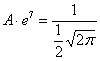
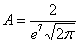
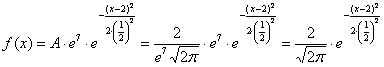
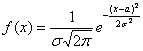
Построим график плотности: 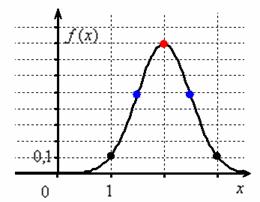
и график функции распределения 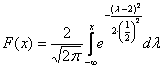
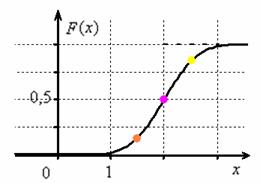
Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке 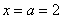
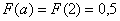
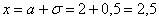
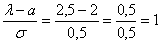
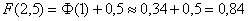
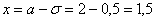
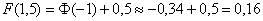
После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.
Да, и ещё нужно вычислить:
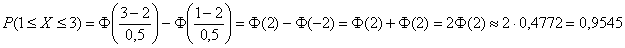
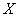
Ответ:
Но этим, конечно, всё дело не ограничивается! Дополнительные примеры, причём довольно творческие, можно найти в тематической pdf-книжке.
И в заключение урока обещанный секрет:
понятие о центральной предельной теореме
которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина 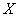
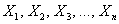
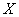
В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение (близкое к нему) и встречается буквально на каждом шагу.
Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально.
Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, длина их лапок тоже распределена по нормальному закону.
Теперь вернёмся к знакомой задаче, где проводится 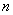
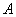
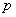
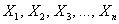
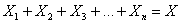
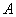
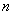
Уже при 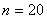
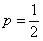
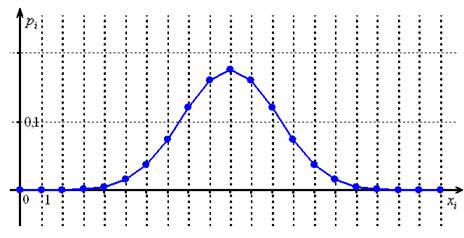
И чем больше 
Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные вероятности соответствующими значениями функций нормального распределения.
Вот такие вот пироги.
Необычайно интересной, и я бы даже сказал «сочной» получилась эта статья, что бывает далеко не всегда, но всегда вдохновляет на новое творчество! Надеюсь, вам тоже понравилось, и вы освоили весь материал «на одном дыхании».
Пример 3. Решение: т.к. случайная величина 
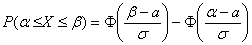
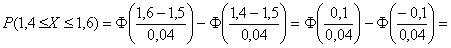
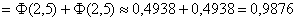
Ответ:
Пример 5. Решение: используем формулу: 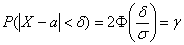
В данной задаче 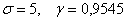
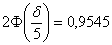
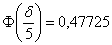
откуда находим:
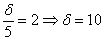
Длина искомого интервала составляет
Ответ: 20 мм
Пример 6. Решение: функция плотности нормально распределённой случайной величины имеет вид 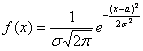
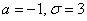
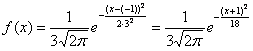
Выполним чертёж: 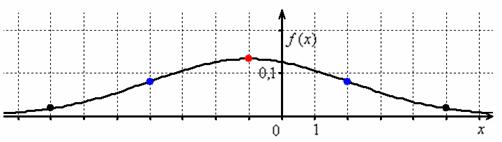
! Примечание: несмотря на то, что условие допускает схематическое построение графика, на чертеже обязательно отображаем все его принципиальные особенности, в частности, на забываем о перегибах в точках 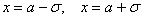
б) Используем формулу 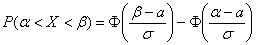
В данной задаче 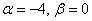
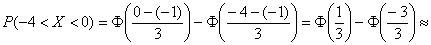
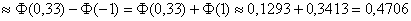
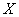
в) Используем формулу 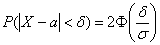
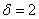
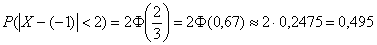
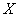
г) Согласно правилу «трех сигм», практически все значения (99,73%) нормально распределенной случайной величины входят в интервал 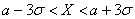
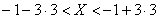
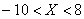
Ответ: а) 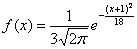
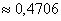
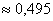
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5