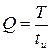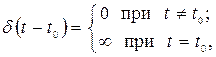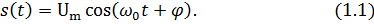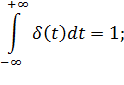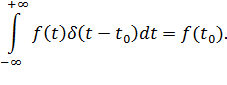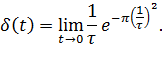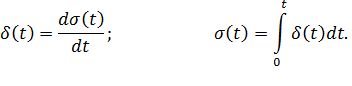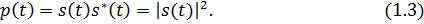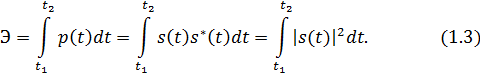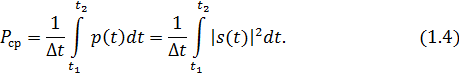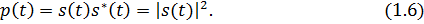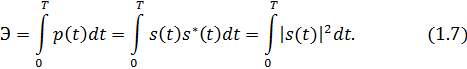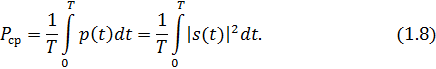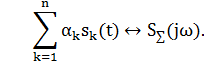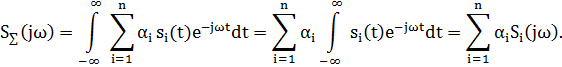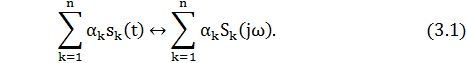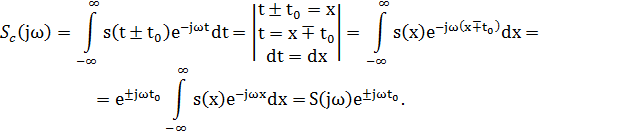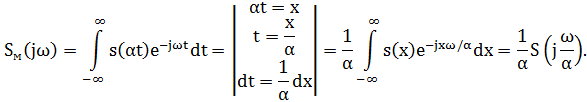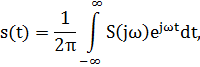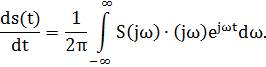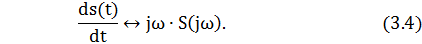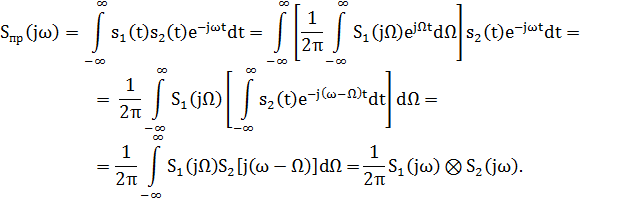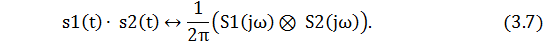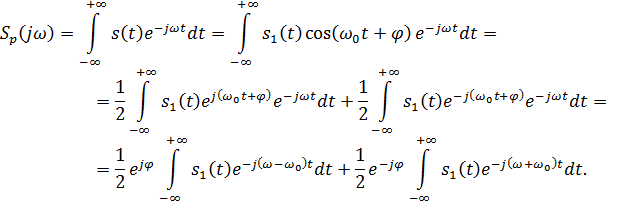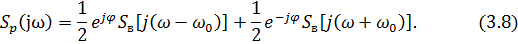для чего нужно знать математическую модель сигнала

Сигнал и его математическая модель

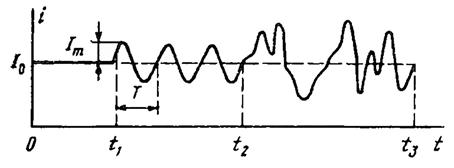
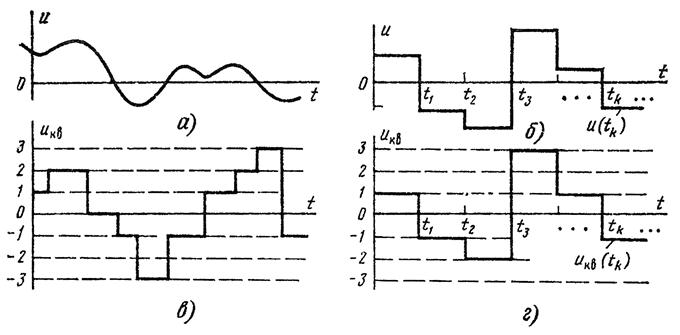
Чаще всего сигнал электросвязи можно рассматривать как меняющуюся во времени электрическую величину (напряжение, ток, электромагнитное колебание, напряженность поля). Эти величины можно наблюдать и регистрировать с помощью различных приборов, например осциллографов. После наблюдения сигнал будет задан в виде графика или таблицы как функция времени. Такое представление называется временной диаграммой. В качестве примера можно привести осциллограмму тока, протекающего через микрофон.

Временная диаграмма тока через микрофон.

На интервале звуковые колебания на микрофон не воздействовали; на интервале – воздействовало звуковое колебание определенного тона; на интервале – сложные звуковые колебания.

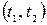
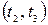
Однако временные диаграммы сигнала являются неудобными как для теоретических расчетов, так и для представления длительных сигналов. Поэтому для проведения всевозможных расчетов с сигналами возникает задача их математического описания. Оно заключается в получении такого относительно простого математического выражения (формулы, уравнения, неравенства и т.д.), по которому можно было бы вычислить необходимые свойства и параметры сигналов (мгновенные значения, числовые характеристики и т.п.). Математическое описание сигнала называется его математической моделью.

Классы сигналов и их математическое представление.

Разделение сигналов на классы производится по следующим признакам:

— форме – простые и сложные;

— информативности – детерминированные и случайные;

— характеристикам – непрерывные, дискретные и цифровые.

Математической моделью простого сигнала является простая функция времени. Из простых сигналов в электросвязи находят применение гармонические сигналы, конечные и бесконечные последовательности прямоугольных импульсов, испытательные сигналы и др.

Гармонический сигнал, который часто называют гармоническим колебанием, записывается в виде

при ,

где – максимальное значение (амплитуда); – циклическая частота; – начальная фаза. Сдвиг по фазе приводит к сдвигу гармонического колебания на время влево. Начальная фаза , циклическая частота . Часто при расчетах используется угловая частота .

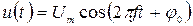
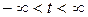
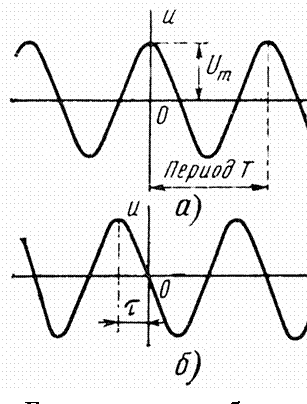
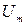
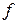
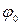
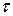
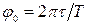
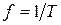
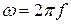
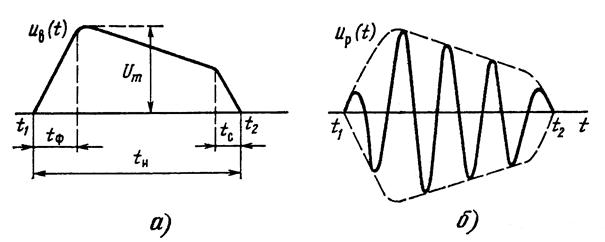
Импульсными сигналами являются сигналы, отличные от нуля в течение ограниченного времени. Эти сигналы существуют лишь в пределах конечного отрезка 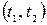. При этом различают видеоимпульсы и радиоимпульсы.

Импульсные сигналы: а) – видеоимпульс; б) – радиоимпульс.

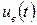
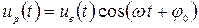
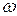
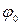
Если – видеоимпульс, то соответствующий ему радиоимпульс (частота и начальная фаза могут быть произвольными).

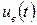
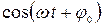
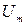
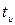
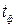
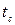
В радиоимпульсе называется огибающей, а функция – заполнением. Параметры видеоимпульса: – амплитуда; – длительность импульса; – длительность фронта импульса; – длительность спада импульса. Происхождение термина «видеоимпульс» связано с тем, что впервые такие импульсы начали применять для описания сигналов в телевидении.

В электросвязи наибольшее применение находят одиночные импульсы или их периодическая последовательность, форма которой приближается к прямоугольной. Для периодической последовательности импульсов, кроме перечисленных параметров, вводится понятие скважности, определяемой как отношение периода к длительности импульса:

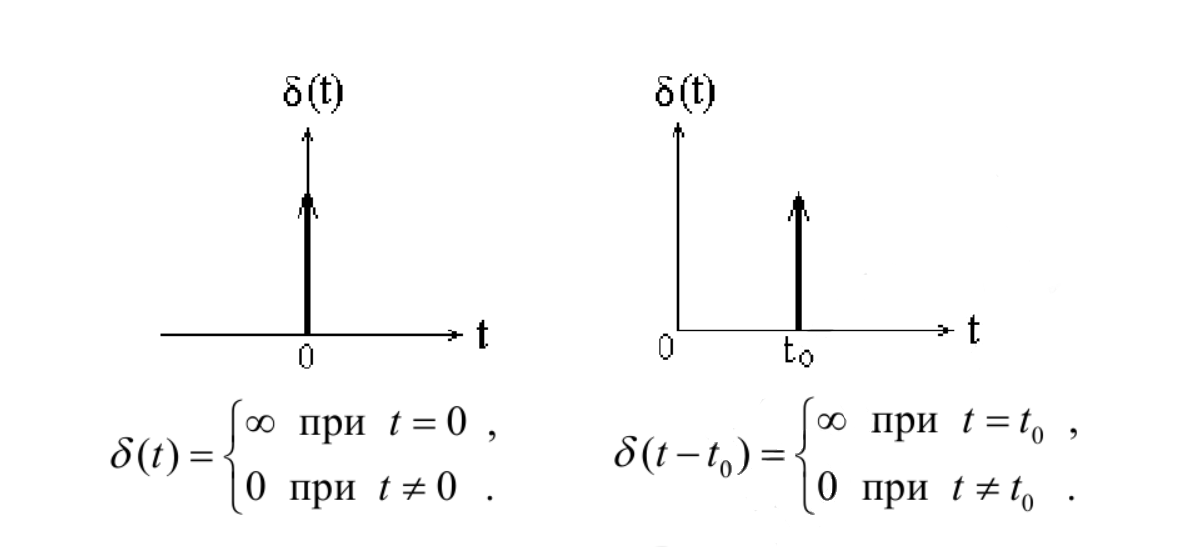
Бесконечно короткий видеоимпульс бесконечной амплитуды называется δ – функцией (дельта – функция), которая записывается в виде:

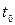
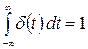
где – момент действия импульса. Эта функция обладает следующим свойством:

,

физически означающим, что хотя значение δ – функции в точке 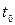и равно бесконечности, но площадь ее конечна и единична.

Широко используется δ – функция при анализе различных радиотехнических цепей. Она является математической моделью прямоугольного импульса малой длительности и большой амплитуды.

Сложные сигналы представляют собой такие функции времени, которые трудно выразить в виде простой математической формулы. Например – отрезок речевого сигнала. Большинство реальных сигналов – это сложные сигналы. Возникает вопрос, как же для них подобрать приемлемое математическое выражение, причем желательно такое, которое подходило бы для большинства сигналов?

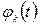
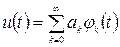
Математиками найдено такое решение. Им широко пользуются в электро– и радиотехнике. Сигнал можно представить в виде ряда некоторых элементарных (простых) функций , называемых базисными:

,

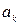
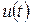
где – коэффициенты разложения, зависящие от сигнала .

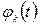
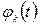
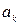
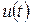
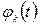
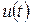
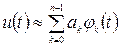
Выбор системы базисных функций зависит от вида сигнала и решаемой задачи. Но имеется общее правило – функции сами должны быть простыми, обеспечивать простое вычисление коэффициентов и давать хорошую сходимость ряда к сигналу . Выбор функции считается тем лучше, чем меньше требуется составляющих ряда для представления сигнала с заданной точностью:

.

Детерминированные и случайные сигналы.

Детерминированным является сигнал, задаваемый функцией времени, по которой можно вычислить его мгновенные значения в любые моменты. Примерами таких сигналов являются гармоническое колебание, видеоимпульсы с известными параметрами. Детерминированные сигналы используются в технике связи как контрольные, испытательные и в качестве переносчика (несущей) для получения модулированных сигналов.

Случайным называется сигнал, математическим описанием которого является случайная функция времени. Физически сигнал можно считать случайным, если невозможно определенно предсказать или вычислить его мгновенные значения. Помехи системы связи чаще всего являются случайными. Сигналы же, в зависимости от обстоятельств, могут быть и детерминированными, и случайными. Случайные сигналы не обязательно являются сложными, они могут быть и простыми.

Непрерывные, дискретные и цифровые сигналы.

Сигналы, которые существуют непрерывно во времени и принимают любые значения из какого – то интервала называются непрерывными. Также непрерывные сигналы называются аналоговыми.

Первоначально в электросвязи использовались преимущественно аналоговые сигналы. Их можно просто генерировать, усиливать, передавать и принимать. Недостатком таких сигналов является то, что любое изменение их формы из – за помех и искажений влечет за собой изменение формы принимаемого сообщения. Возросшие требования к точности воспроизведения сообщений заставили перейти к дискретным и цифровым сигналам.

Дискретные сигналы – это сигналы, принимающие конечное число значений или состояний. Дискретные сигналы могут непосредственно создаваться на выходе преобразователя сообщение – сигнал или образовываться в результате дискретизации аналогового сигнала.

Цифровые сигналы – разновидность дискретных сигналов, когда квантованные отсчетные значения представлены в виде цифр. Цифровыми также являются сигналы, соответствующие кодовым комбинациям на выходе кодера. Преимущество цифровых сигналов – более высокая помехоустойчивость и возможность их формирования и обработки микроэлектронными логическими устройствами. Цифровые сигналы находят все большее применение в новых системах электросвязи.

Сигналы: а) – непрерывные; б) – дискретные по времени; в) – квантованные по уровню и непрерывные по времени; г) – квантованные по уровню и дискретные по времени.

Источник

Математические модели сигналов

РЕФЕРАТ

Тема курсовой работы – «Расчёт спектральных характеристик радиотехнических сигналов».

Курсовая работа выполнена на 37 листах пояснительной записки, 2 листах формата А3, содержащий графики сигналов и их амплитудных.

В первом разделе пояснительной записки, а именно в разделе «Сигналы и их характеристики», проанализированы виды сигналов и их характеристики.

Во втором разделе пояснительной записки, а именно в разделе «Характеристики сигналов в частотной области», рассматриваются характеристики радиотехнических сигналов, рассматриваются ряды Фурье.

В третьем разделе пояснительной записки, а именно в разделе «Свойства преобразований Фурье», рассматриваются свойства преобразований Фурье.

В четвертом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик одиночного видеоимпульса», описывается процесс расчёта спектральных характеристик одиночного видеоимпульса.

В пятом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик одиночного радиоимпульса», описывается процесс расчёта спектральных характеристик одиночного радиоимпульса.

В шестом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик периодической последовательности видеоимпульсов», описывается процесс расчёта спектральных характеристик периодической последовательности видеоимпульсов.

В седьмом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик периодической последовательности радиоимпульсов», описывается процесс расчёта спектральных характеристик периодической последовательности радиоимпульсов.

Курсовая работа содержит заключение о проделанной работе.

СОДЕРЖАНИЕ

1 Сигналы и их характеристики7

1.1 Радиотехнические сигналы7

1.2 Математические модели сигналов7

1.3 Классификация сигналов8

1.3.1 Управляющие модулирующие сигналы8

1.3.2 Испытательные сигналы10

1.4 Характеристики сигналов13

2 Характеристики сигналов в частотной области15

3 Свойства преобразование Фурье17

4 Расчет спектральных характеристик одиночного видеоимпульса22

5 Расчет спектральных характеристик одиночного радиоимпульса25

6 Расчет спектральных характеристик периодической последовательности видеоимпульсов28

7 Расчет спектральных характеристик периодической последовательности радиоимпульсов31

Список используемых источников36

ВВЕДЕНИЕ

Теоретические основы радиотехники – это базовая дисциплина в системе профессиональной подготовки специалистов в области радиотехники, радиоэлектроники, радиоинформатики. Ее основной целью является изучение методов и технических средств формирования и обработки радиотехнических сигналов, что необходимо для решения конкретных практических задач в области радиотехники, в частности для создания современных радиотехнических систем, состоящих из большого количества различных устройств.

При разработке и исследовании радиотехнических устройств различного уровня сложности и назначения возникают задачи, связанные с анализом и синтезом устройств. В наиболее общем виде данные задачи могут быть сформулированы следующим образом.

Задача анализа: заданы радиотехническое устройство, входной сигнал и их основные характеристики; необходимо определить выходной сигнал и его характеристики. Поскольку устройство представляет собой различные комбинации линейных и нелинейных звеньев, то задача по существу сводится к анализу прохождения сигнала через линейные и нелинейные устройства. Требуемый уровень адекватности результатов анализа реальному положению вещей, а также количественные характеристики, подлежащие расчету, определяются тем критерием, по которому оценивается качество работы устройства.

Задача синтеза заданы входной сигнал и его основные характеристики, а также выходной сигнал с требуемыми для проектировщика характеристиками; необходимо разработать радиотехническое устройство, которое преобразует входной сигнал с заданными характеристиками в сигнал с желаемыми характеристиками. Частным вариантом задачи синтеза является случай, когда входной сигнал отсутствует и требуется создать устройство для формирования (генерирования) сигнала с желаемыми характеристиками. Основным результатом синтеза являются оптимальные алгоритмы и структурные схемы проектируемого устройства. Синтез устройства не исключает необходимости выполнения некоторых процедур анализа в ходе оценки его работоспособности при возможных отклонениях от принятых априорных данных.

При решении задач анализа и синтеза объектами исследования являются сигнал и радиотехническое устройство. Успешное решение этих задач предполагает хорошую ориентацию исследователя и проектировщика во множестве сигналов, способов их аналогового и дискретного представления, методах анализа в частотной и временной областях. Самостоятельное значение имеют вопросы обработки сигналов, включающие в себя методы и технические средства формирования и различных преобразований сигналов. Технические средства – это и есть радиотехнические устройства (цепи), решающие обширный ассортимент задач и характеризуемые многообразием структурной и функциональной организации. Это требует систематизации знаний в области современных методов (уже ставших классическими) физико-математического анализа процессов формирования сигналов, а также их линейных и нелинейных преобразований.

Задачей курсовой работы является расчет спектральных характеристик радиотехнических сигналов. Для решения этой задачи необходимо:

— рассмотреть и проанализировать виды сигналов;

— рассмотреть и проанализировать основные характеристики сигналов в частотной области;

— рассмотреть и проанализировать свойства преобразования Фурье;

— рассмотреть и проанализировать свойства линейности, сдвига сигнала, спектр производной и интеграла, спектр радиоимпульса.

СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ

Радиотехнические сигналы

Сигнал – физический процесс, являющийся функцией некоторых параметров и используемый в качестве носителя информации. В радиотехнике изучают две группы электрических сигналов: детерминированные и случайные.

Детерминированные сигналы– это сигналы, мгновенные значения которых в любой момент времени известны, т.е. предсказуемы с вероятностью, равной единице. Они могут быть описаны определенными функциями времени. Анализ и исследование этих сигналов осуществляется с помощью математического аппарата, не связанного с теорией вероятностей. Примером такого сигнала является косинусоидальное колебание, описываемое функцией

где U_m – амплитуда сигнала; ω₀ = 2πf₀ – угловая частота сигнала; φ – начальная фаза сигнала.

Случайные сигналы – это сигналы, мгновенные значения которых в любые моменты времени неизвестны и не могут быть предсказаны с вероятностью, равной единице. Как ни парадоксально на первый взгляд, но сигналом, несущим полезную информацию, может быть только случайный сигнал. Информация в нем заложена во множестве амплитудных, частотных (фазовых) или кодовых изменений передаваемого сигнала. На практике любой радиотехнический сигнал, в котором заложена полезная информация, должен рассматриваться как случайный.

Большинство используемых на практике радиотехнических сигналов относится к классу случайных по двум причинам. Во-первых, любой сигнал, являющийся носителем информации, должен рассматриваться как случайный. Во-вторых, в устройствах, которые «работают» с сигналами, практически всегда имеются шумы или помехи, которые накладываются на полезный сигнал. Поэтому в любом канале связи полезный сигнал искажается при передаче и сообщении на приемной стороне воспроизводится с некоторой ошибкой.

Непреодолимой границы между детерминированными и случайными сигналами нет. В условиях большого отношения полезного сигнала к шуму, т.е. в случае, когда уровень помех значительно меньше уровня полезного сигнала, детерминированная модель сигнала адекватна реальной ситуации. При этом можно применять методы анализа неслучайных сигналов.

Классификация сигналов

Для представления и анализа сигналов приходится применять различные методы, которые зависят от назначения, структуры, математического описания и других свойств сигналов. Поэтому достаточно важным этапом процедуры анализа является классификация радиотехнических сигналов.

Классификацию детерминированных сигналов можно производить по различным признакам. Как известно, для передачи информации на расстояние используются модулированные колебания, т.е. высокочастотные колебания, один или несколько параметров которых изменяются по закону передаваемого сообщения. Поэтому в канале связи различают следующие сигналы:

— управляющие (модулирующие) сигналы;

— высокочастотные (несущие) гармонические колебания;

— модулированные колебания (радиосигналы).

Испытательные сигналы

Сигнал называется испытательным, так как он применяется для получения импульсной характеристики радиотехнического устройства. Реакция устройства на дельта-функцию – это и есть его импульсная характеристика.

Рисунок 1.4 – Дельта-функция

Свойства дельта-функции, благодаря которым она широко используется в математике, физике и радиотехнике:

1) площадь сигнала, описываемого -функцией, равна 1 т.е.

2) селектирующее свойство

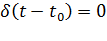
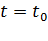
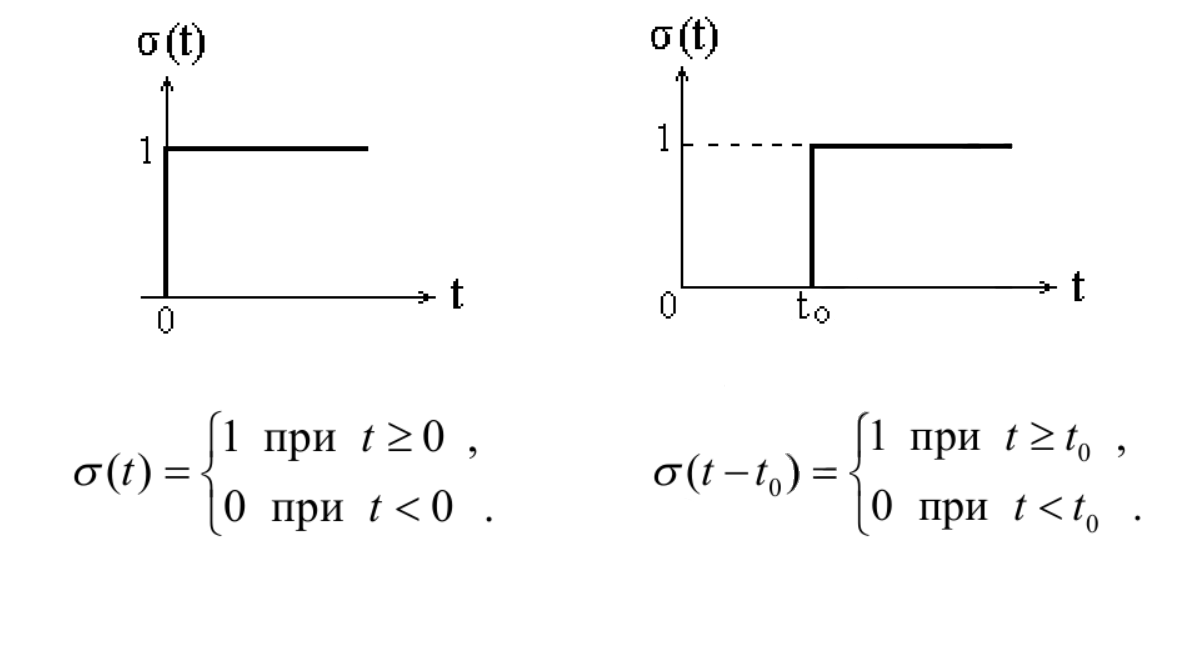
Селектирующее свойство становится понятным, если учесть, что на всей оси времени, кроме точки . Это позволяет сделать интервал интегрирования бесконечно малым в окрестности точки t₀. В этом интервале функция f(t) принимает значение f(t₀), позволяющее ее вынести за знак интеграла.

б. Функция единичного скачка

Функция единичного скачка (функция Хевисайда) описывает процесс резкого (мгновенного) перехода физического устройства из одного состояния в другое. На рис. 1.5 приведен график этой функции.

Сигнал называется испытательным, так как он применяется для получения переходной характеристики радиотехнического устройства. Реакция устройства на единичную функцию – это и есть его переходная характеристика.

Рисунок 1.5 – Функция единичного скачка

Связь между функция 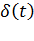и

в. Гармонический сигнал

Гармонический сигнал также является испытательным сигналом, так как с его помощью определяются частотные характеристики устройств.

Характеристики сигналов

Для сигнала, существующего в интервале t=t₂-t₁, наиболее важными являются следующие характеристики (предполагаем, что сигнал представлен в комплексной форме):

1. Среднее значение сигнала

Среднее значение сигнала – это по существу его постоянная составляющая.

2. Мгновенная мощность сигнала

4. Средняя мощность сигнала

Для периодического сигнала, энергия которого равна бесконечности, среднее значение и энергетические характеристики определяются в пределах одного периода:

1. Среднее значение сигнала

2. Мгновенная мощность сигнала

4. Средняя мощность сигнала

В данном разделе были рассмотрены виды сигналов и их характеристики.

СВОЙСТВА ПРЕОБРАЗОВАНИЙ ФУРЬЕ

Формулы прямого и обратного преобразования Фурье позволяют по сигналу s(t) определить его спектральную плотность S(jω) и, если в этом есть необходимость, по известной спектральной плотности S(jω) определить сигнал s(t). Для обозначения этого соответствия между сигналом и его спектром применяется символ s(t)↔ S(jω).

С помощью свойств преобразований Фурье можно определить спектр измененного сигнала, преобразуя спектр первоначального сигнала.

Воспользуемся прямым преобразованием Фурье

Вывод: прямое преобразование Фурье, является линейной операцией, обладает свойствами однородности и аддитивности. Поэтому спектр суммы сигналов равен сумме спектров.

2. Спектр сигнала, сдвинутого во времени

(3.2)

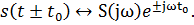
Вывод: сдвиг сигнала во времени на величину ±t₀ приводит к изменению фазовой характеристики спектра на величину ±ωt₀. Амплитудный спектр не изменяется.

3. Изменение масштаба во времени

Вывод: при сжатии (расширении) сигнала во времени в определенное число во столько же раз расширяется (сжимается) его спектр по оси частот при пропорциональном уменьшении (увеличении) амплитуд его составляющих.

4. Спектр производной

Для определения спектра производной сигнала возьмем производную по времени от правой и левой части обратного преобразования Фурье:

6. Спектр произведения двух сигналов

Найдем спектр произведения двух сигналов с помощью обратного преобразования Фурье

Вывод: Спектр произведения двух сигналов равен свертке их спектров, умноженной на коэффициент 1/(2π).

7. Свойство дуальности

Если сигналу s(t) соответствует амплитудный спектр S(ω), то сигналу, имеющему форму такую же, как форма амплитудного спектра S(ω), соответствует спектр, имеющий форму сигнала s(t).

8. Смещение спектра сигнала

Произведение двух сигналов s₁(t) и s₂(t)= cos(ω₀t+ φ) образует гармонический сигнал s(t)= s₁(t)cos(ω₀t+ φ). Так если s₁(t) – видеоимпульс, то s(t) – это радиоимпульс с несущей частотой ω₀.

Определим спектральную плотность сигнала s(t):

Таким образом, спектральная плотность сигнала s_р(t) равна

Вывод: При умножении сигнала на гармоническую функцию образуется сигнал, спектр которого представляет собой преобразованный спектр сигнала s₁(t). Суть преобразования заключается в переносе спектра на ±ω₀ с уменьшением вдвое его величины.

Рассмотренные свойства преобразования Фурье значительно облегчают вычисление спектров различных сигналов.

ЗАКЛЮЧЕНИЕ

Во время выполнения курсовой работы, был произведен расчет амплитудного и фазового спектров одиночных видео- и радиоимпульсов, и периодических последовательностей видео- и радиоимпульсов.

В ходе решения данной задачи был определен спектр одиночного видеоимпульса при помощи прямого преобразования Фурье. При помощи свойств преобразования Фурье также были рассчитаны спектры других сигналов.

В ходе выполнения курсовой работы убедились в том, что свойства преобразований Фурье упрощают расчёт спектров непериодических сигналов.

Данная работа подтверждает, что спектр периодического сигнала дискретен, а непериодического сигнала сплошной.

ПРИЛОЖЕНИЕ

РЕФЕРАТ

Тема курсовой работы – «Расчёт спектральных характеристик радиотехнических сигналов».

Курсовая работа выполнена на 37 листах пояснительной записки, 2 листах формата А3, содержащий графики сигналов и их амплитудных.

В первом разделе пояснительной записки, а именно в разделе «Сигналы и их характеристики», проанализированы виды сигналов и их характеристики.

Во втором разделе пояснительной записки, а именно в разделе «Характеристики сигналов в частотной области», рассматриваются характеристики радиотехнических сигналов, рассматриваются ряды Фурье.

В третьем разделе пояснительной записки, а именно в разделе «Свойства преобразований Фурье», рассматриваются свойства преобразований Фурье.

В четвертом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик одиночного видеоимпульса», описывается процесс расчёта спектральных характеристик одиночного видеоимпульса.

В пятом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик одиночного радиоимпульса», описывается процесс расчёта спектральных характеристик одиночного радиоимпульса.

В шестом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик периодической последовательности видеоимпульсов», описывается процесс расчёта спектральных характеристик периодической последовательности видеоимпульсов.

В седьмом разделе пояснительной записки, а именно в разделе «Расчёт спектральных характеристик периодической последовательности радиоимпульсов», описывается процесс расчёта спектральных характеристик периодической последовательности радиоимпульсов.

Курсовая работа содержит заключение о проделанной работе.

СОДЕРЖАНИЕ

1 Сигналы и их характеристики7

1.1 Радиотехнические сигналы7

1.2 Математические модели сигналов7

1.3 Классификация сигналов8

1.3.1 Управляющие модулирующие сигналы8

1.3.2 Испытательные сигналы10

1.4 Характеристики сигналов13

2 Характеристики сигналов в частотной области15

3 Свойства преобразование Фурье17

4 Расчет спектральных характеристик одиночного видеоимпульса22

5 Расчет спектральных характеристик одиночного радиоимпульса25

6 Расчет спектральных характеристик периодической последовательности видеоимпульсов28

7 Расчет спектральных характеристик периодической последовательности радиоимпульсов31

Список используемых источников36

ВВЕДЕНИЕ

Теоретические основы радиотехники – это базовая дисциплина в системе профессиональной подготовки специалистов в области радиотехники, радиоэлектроники, радиоинформатики. Ее основной целью является изучение методов и технических средств формирования и обработки радиотехнических сигналов, что необходимо для решения конкретных практических задач в области радиотехники, в частности для создания современных радиотехнических систем, состоящих из большого количества различных устройств.

При разработке и исследовании радиотехнических устройств различного уровня сложности и назначения возникают задачи, связанные с анализом и синтезом устройств. В наиболее общем виде данные задачи могут быть сформулированы следующим образом.

Задача анализа: заданы радиотехническое устройство, входной сигнал и их основные характеристики; необходимо определить выходной сигнал и его характеристики. Поскольку устройство представляет собой различные комбинации линейных и нелинейных звеньев, то задача по существу сводится к анализу прохождения сигнала через линейные и нелинейные устройства. Требуемый уровень адекватности результатов анализа реальному положению вещей, а также количественные характеристики, подлежащие расчету, определяются тем критерием, по которому оценивается качество работы устройства.

Задача синтеза заданы входной сигнал и его основные характеристики, а также выходной сигнал с требуемыми для проектировщика характеристиками; необходимо разработать радиотехническое устройство, которое преобразует входной сигнал с заданными характеристиками в сигнал с желаемыми характеристиками. Частным вариантом задачи синтеза является случай, когда входной сигнал отсутствует и требуется создать устройство для формирования (генерирования) сигнала с желаемыми характеристиками. Основным результатом синтеза являются оптимальные алгоритмы и структурные схемы проектируемого устройства. Синтез устройства не исключает необходимости выполнения некоторых процедур анализа в ходе оценки его работоспособности при возможных отклонениях от принятых априорных данных.

При решении задач анализа и синтеза объектами исследования являются сигнал и радиотехническое устройство. Успешное решение этих задач предполагает хорошую ориентацию исследователя и проектировщика во множестве сигналов, способов их аналогового и дискретного представления, методах анализа в частотной и временной областях. Самостоятельное значение имеют вопросы обработки сигналов, включающие в себя методы и технические средства формирования и различных преобразований сигналов. Технические средства – это и есть радиотехнические устройства (цепи), решающие обширный ассортимент задач и характеризуемые многообразием структурной и функциональной организации. Это требует систематизации знаний в области современных методов (уже ставших классическими) физико-математического анализа процессов формирования сигналов, а также их линейных и нелинейных преобразований.

Задачей курсовой работы является расчет спектральных характеристик радиотехнических сигналов. Для решения этой задачи необходимо:

— рассмотреть и проанализировать виды сигналов;

— рассмотреть и проанализировать основные характеристики сигналов в частотной области;

— рассмотреть и проанализировать свойства преобразования Фурье;

— рассмотреть и проанализировать свойства линейности, сдвига сигнала, спектр производной и интеграла, спектр радиоимпульса.

СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ

Радиотехнические сигналы

Сигнал – физический процесс, являющийся функцией некоторых параметров и используемый в качестве носителя информации. В радиотехнике изучают две группы электрических сигналов: детерминированные и случайные.

Детерминированные сигналы– это сигналы, мгновенные значения которых в любой момент времени известны, т.е. предсказуемы с вероятностью, равной единице. Они могут быть описаны определенными функциями времени. Анализ и исследование этих сигналов осуществляется с помощью математического аппарата, не связанного с теорией вероятностей. Примером такого сигнала является косинусоидальное колебание, описываемое функцией

где U_m – амплитуда сигнала; ω₀ = 2πf₀ – угловая частота сигнала; φ – начальная фаза сигнала.

Случайные сигналы – это сигналы, мгновенные значения которых в любые моменты времени неизвестны и не могут быть предсказаны с вероятностью, равной единице. Как ни парадоксально на первый взгляд, но сигналом, несущим полезную информацию, может быть только случайный сигнал. Информация в нем заложена во множестве амплитудных, частотных (фазовых) или кодовых изменений передаваемого сигнала. На практике любой радиотехнический сигнал, в котором заложена полезная информация, должен рассматриваться как случайный.

Большинство используемых на практике радиотехнических сигналов относится к классу случайных по двум причинам. Во-первых, любой сигнал, являющийся носителем информации, должен рассматриваться как случайный. Во-вторых, в устройствах, которые «работают» с сигналами, практически всегда имеются шумы или помехи, которые накладываются на полезный сигнал. Поэтому в любом канале связи полезный сигнал искажается при передаче и сообщении на приемной стороне воспроизводится с некоторой ошибкой.

Непреодолимой границы между детерминированными и случайными сигналами нет. В условиях большого отношения полезного сигнала к шуму, т.е. в случае, когда уровень помех значительно меньше уровня полезного сигнала, детерминированная модель сигнала адекватна реальной ситуации. При этом можно применять методы анализа неслучайных сигналов.

Математические модели сигналов

Для того чтобы сигналы являлись объектами теоретического изучения и анализа, необходимо иметь их математические модели. Математическая модель сигнала – это формализованное его представление в виде определенного математического объекта. Физической величиной, определяющей характер радиотехнического сигнала, обычно является напряжение или ток, изменяющиеся во времени по определенному закону. Поэтому наиболее часто в качестве модели сигнала используется функциональная зависимость, аргументом которой является время, т.е. функция времени. В радиотехнике математической моделью сигнала является функция времени, обозначается s ( t ), u ( t ), i ( t ).

Целесообразность использования комплексной формы представления сигнала обусловлена удобством выполнения некоторых математических преобразований. В качестве математической модели сигнала используется также функциональная зависимость, аргументом которой является циклическая f или угловая ω частота, т.е. сигнал рассматривается как функция частоты. Эта функциональная зависимость, являющаяся по существу спектральным представлением сигнала, получила название спектра сигнала. Такое представление сигнала чаще рассматривают не как собственно сигнал, а как характеристику сигнала в частотной области. Сигналы могут быть представлены также в графическом и табличном виде.

Классификация сигналов

Для представления и анализа сигналов приходится применять различные методы, которые зависят от назначения, структуры, математического описания и других свойств сигналов. Поэтому достаточно важным этапом процедуры анализа является классификация радиотехнических сигналов.

Классификацию детерминированных сигналов можно производить по различным признакам. Как известно, для передачи информации на расстояние используются модулированные колебания, т.е. высокочастотные колебания, один или несколько параметров которых изменяются по закону передаваемого сообщения. Поэтому в канале связи различают следующие сигналы:

— управляющие (модулирующие) сигналы;

— высокочастотные (несущие) гармонические колебания;

Источник