для чего нужны булевы функции
Булева функция
Категории Дискретная математика | Под редакцией сообщества: Математика
Булева функция (функция алгебры логики) — функция, определённая на множестве упорядоченных наборов из нулей и единиц и принимающиая на каждом из этих наборов значение 0 или 1.
Булевы функции получили своё название по имени английского математика Дж. Буля (02.11.1815–08.12.1864). С давних времён эти функции играют важную роль в вопросах оснований математики и математической логике. С середины 20-го века булевы функции широко используются в различных теоретических и прикладных задачах дискретной математики и математической кибернетики.
Содержание
↑Задание функций таблицами
Пусть E = <0, 1>, X— некоторое счётное множество переменных, E n — множество всех наборов (α1, …, αn) из нулей и единиц, n ≥ 1. Пусть f ( n ) — отображение множества E n в E, n ≥ 1, x1, …, xn — переменные из множества X, и пусть функция f ( n ) (x1, …, xn) задаёт это отображение, где E n — область определения, E — область значений, x1, …, xn — переменные, от которых зависит f ( n ) (x1, …, xn). Функция f ( n ) (x1, …, xn) называется n-местной булевой функцией (или функцией алгебры логики), а f ( n ) — n-местным функциональным символом, соответствующим этой функции. Верхние индексы у функциональных символов, как правило, опускаются, однако при этом указывается число переменных, от которых зависят рассматриваемые функции.
С теоретико-множественной точки зрения функция алгебры логики f (x1, …, xn) — это не просто отображение множества всех наборов длины n из нулей и единиц в множество <0, 1>, а совокупность такого отображения и упорядоченного набора x1, …, xn переменных. В этом смысле функции f (x1, x2, x3) и f (x2, x1, x3), вообще говоря, различны, хотя и определяются одним и тем же отображением <0, 1>3 → <0, 1>. В соответствии с этим возникает следующее понятие равенства функций: функции равны, если они зависят от одного и того же множества переменных и задают одно и то же отображение. А именно, булевы функции f ( x1, …, xn) и g (x1, …, xn) называются равными (обозначение f = g), если f (α1, …, αn) = g (α1, …, αn) для любого набора (α1, …, αn) из нулей и единиц.
Рассмотрим некоторые функции одного и двух аргументов, которые являются в определенном смысле аналогами « элементарных функций» в арифметике, алгебре и математическом анализе.
При n = 1 будет всего 4 функции, указанные в табл.1, где 0 — константа 0, x — тождественная функция, ¬ x — отрицание x, 1 — константа 1.
Булевы функции
Содержание
1 Понятие булевой функции
Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:
| x 1 | x 2 | . | x n- 1 | x n | f |
|---|---|---|---|---|---|
| 0 | 0 | . | 0 | 0 | f(0,0. 0,0) |
| 0 | 0 | . | 0 | 1 | f(0,0. 0,1) |
| 0 | 0 | . | 1 | 0 | f(0,0. 1,0) |
| 0 | 0 | . | 1 | 1 | f(0,0. 1,1) |
| . | . | . | . | . | . |
| 1 | 1 | . | 0 | 0 | f(1,1. 0,0) |
| 1 | 1 | . | 0 | 1 | f(1,1. 0,1) |
| 1 | 1 | . | 1 | 0 | f(1,1. 1,0) |
| 1 | 1 | . | 1 | 1 | f(1,1. 1,1) |
| x | 0 | x | ¬ x | 1 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:
| x 1 | x 2 | x 1 & x 2 | x 1 Ъ x 2 | x 1 Й x 2 | x 1 Е x 2 | x 1 є x 2 | x 1 | x 2 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
2 Суперпозиция функций
Пример 1 (суперпозиция функций).
Суперпозицию ( x & y ) Е ( ¬x Ъ ¬y ) можно прочитать как « x и y плюс не x или не y ».
3 Двойственные функции
Пример 2 (двойственные функции).
Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.
Пример 3 (вектор двойственной функции).
4 Разложение функции по переменным
Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.
Следствие 1 (Совершенная дизъюнктивная нормальная форма).
Любая функция f может быть представлена в следующей форме: *
Следствие 2 (Совершенная конъюнктивная нормальная форма).
Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.
Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.
Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.
Пример 4 (совершенная дизъюнктивная нормальная форма).
Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Определение булевой функции
Содержание
Основные сведения [ править ]
| Таблица истинности | |||||
|---|---|---|---|---|---|
| [math]x_1[/math] | [math]x_2[/math] | [math]\ldots[/math] | [math]x_n[/math] | [math]f(x_1,x_2,\ldots,x_n)[/math] | |
| [math]0[/math] | [math]0[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(0,0,\ldots,0)[/math] | |
| [math]1[/math] | [math]0[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(1,0,\ldots,0)[/math] | |
| [math]0[/math] | [math]1[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(0,1,\ldots,0)[/math] | |
| [math]1[/math] | [math]1[/math] | [math]\ldots[/math] | [math]0[/math] | [math]f(1,1,\ldots,0)[/math] | |
| [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | [math]\vdots[/math] | |
| [math]0[/math] | [math]1[/math] | [math]\ldots[/math] | [math]1[/math] | [math]f(0,1,\ldots,1)[/math] | |
| [math]1[/math] | [math]1[/math] | [math]\ldots[/math] | [math]1[/math] | [math]f(1,1,\ldots,1)[/math] | |
Практически все булевы функции малых арностей ( [math]0, 1, 2[/math] и [math]3[/math] ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).
Нульарные функции [ править ]
Унарные функции [ править ]
Таблица значений булевых функций от одной переменной:
| Функции от одной переменной | ||||
|---|---|---|---|---|
| [math]0[/math] | [math]x[/math] | [math]\neg x[/math] | [math]1[/math] | |
| 0 | [math]0[/math] | [math]0[/math] | [math]1[/math] | [math]1[/math] |
| 1 | [math]0[/math] | [math]1[/math] | [math]0[/math] | [math]1[/math] |
| Сохраняет 0 | ✓ | ✓ | ||
| Сохраняет 1 | ✓ | ✓ | ||
| Самодвойственная | ✓ | ✓ | ||
| Монотонная | ✓ | ✓ | ✓ | |
| Линейная | ✓ | ✓ | ✓ | ✓ |
Названия булевых функций от одной переменной:
| Обозначение | Название |
|---|---|
| [math]0[/math] | тождественный ноль, тождественная ложь, тождественное «НЕТ» |
| [math]x[/math] | тождественная функция, логическое «ДА», «YES»(англ.) |
| [math]\bar x,\ \neg x,\ x'[/math] | отрицание, логическое «НЕТ», «НЕ», «НИ», «NOT»(англ.), «NO»(англ.) |
| [math]1[/math] | тождественная единица, тождественная истина, тождественное «ДА», тавтология |
Бинарные функции [ править ]
Таблица значений булевых функций от двух переменных:
| Функции от двух переменных: | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | [math]0[/math] | [math]x \land y[/math] | [math]x \nrightarrow y[/math] | [math]x[/math] | [math]x \nleftarrow y[/math] | [math]y[/math] | [math]x \oplus y[/math] | [math]x \lor y[/math] | [math]x \downarrow y[/math] | [math]x = y[/math] | [math]\neg y[/math] | [math]x \leftarrow y[/math] | [math]\neg x[/math] | [math]x \rightarrow y[/math] | [math]x \triangledown y[/math] | [math]1[/math] |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Сохраняет 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Сохраняет 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Самодвойственная | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| Монотонная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Линейная | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
Названия булевых функций от двух переменных:
| Обозначение | Другие обозначения | Название |
|---|---|---|
| [math]0[/math] | тождественный ноль, тождественная ложь, тождественное «НЕТ» | |
| [math]x \land y[/math] | [math]x \cdot y,\ xy,\ x \And y,\ x\ AND\ y,\ AND(x, y),\ min(x, y), x [/math] И [math]y,[/math] И [math](x, y)[/math] | 2И, конъюнкция |
| [math]x \nrightarrow y[/math] | [math]x \gt y,\ \neg(x \rightarrow y),\ x\ GT\ y,\ GT(x,\ y)[/math] | больше, инверсия прямой импликации |
| [math]x[/math] | [math]YES1(x,y),[/math] ДА1 [math](x, y)[/math] | первый операнд |
| [math]x \nleftarrow y[/math] | [math]x \lt y,\ \neg(x \leftarrow y),\ x\ LT\ y,\ LT(x, y)[/math] | меньше, инверсия обратной импликации |
| [math]y[/math] | [math]YES2(x, y),[/math] ДА2 [math](x, y)[/math] | второй операнд |
| [math]x \oplus y[/math] | [math]x + _2 y,\ x \not = y,\ x \gt \lt y,\ x \lt \gt y,\ x\ XOR\ y,\ XOR(x,y)[/math] | сложение по модулю 2, не равно, ксор, исключающее «или» |
| [math]x \lor y[/math] | [math]x + y,\ x\ OR\ y,\ OR(x,y),\ max(x,y),[/math] [math]x [/math] ИЛИ [math]y,[/math] ИЛИ [math](x, y)[/math] | 2ИЛИ, дизъюнкция |
| [math]x \downarrow y[/math] | [math]x\ NOR\ y,\ NOR(x,y)[/math] [math]x [/math] ИЛИ-НЕ [math]y,[/math] ИЛИ-НЕ [math](x, y)[/math] | НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса |
| [math]x = y[/math] | [math]x \equiv y, x EQV y, EQV(x,y), x \sim y, x \leftrightarrow y[/math] | равенство, эквивалентность |
| [math]\neg y[/math] | [math]NOT2(x, y),\ y’,\ \bar | отрицание (негация, инверсия) второго операнда |
| [math]x \leftarrow y[/math] | [math]x \geq y,\ x \subset y,\ x\ GE\ y,\ GE(x, y)[/math] | больше или равно, обратная импликация (от второго аргумента к первому) |
| [math]\neg x[/math] | [math]NOT1(x,y),\ x’,\ \bar | отрицание (негация, инверсия) первого операнда |
| [math]x \rightarrow y[/math] | [math]x \leq y,\ x \supset y,\ x\ LE\ y,\ LE(x,y)[/math] | меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму) |
| [math]x \triangledown y[/math] | [math]x \mid y,\ x\ NAND\ y,\ NAND(x,y),[/math] [math]x [/math] И-НЕ [math]y,[/math] И-НЕ [math](x, y)[/math] | НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера |
| [math]1[/math] | тождественная единица, тождественная истина, тождественное «ДА», тавтология |
Тернарные функции [ править ]
| Таблица истинности некоторых тернарных функций | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [math]x[/math] | [math]y[/math] | [math]z[/math] | [math]x \downarrow y \downarrow z[/math] | [math]\neg (\geq 2(x,y,z))[/math] | [math]x \not = y \not = z[/math] | [math]x \mid y \mid z[/math] | [math]min(x,y,z)[/math] | [math]x=y=z[/math] | [math]x \oplus y \oplus z[/math] | [math]\geq 2(x,y,z)[/math] | [math]f_1[/math] | [math]f_2[/math] | [math]max(x,y,z)[/math] |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Названия булевых функций трех переменных:
| Обозначения | Другие обозначения | Названия |
|---|---|---|
| [math]x \downarrow y \downarrow z[/math] | [math]\downarrow (x,y,z) = Webb_2 (x,y,z)[/math] | 3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса |
| [math]\neg (\geq 2(x,y,z))[/math] | Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией | |
| [math]x \not = y \not = z[/math] | [math][\not =(x,y,z)] = NE(x,y,z)[/math] | Неравенство |
| [math]x \mid y \mid z[/math] | [math]\mid(x,y,z)[/math] | 3-И-НЕ, штрих Шеффера |
| [math]x \land y \land z[/math] | [math]\land (x,y,z) = (x\ AND\ y\ AND\ z) = AND(x,y,z) = min(x,y,z) = \lt br/\gt (x[/math] И [math] y[/math] И [math] z) = [/math] И [math](x,y,z)[/math] | 3-И, минимум |
| [math]x=y=z[/math] | [math][=(x,y,z)] = EQV(x,y,z)[/math] | Равенство |
| [math]x \oplus y \oplus z[/math] | [math]x +_2 y +_2 z = \oplus (x,y,z) = +_2 (x,y,z)[/math] | Тернарное сложение по модулю 2 |
| [math]\geq 2(x,y,z)[/math] | [math](x [/math] И [math]y) [/math] ИЛИ [math](y[/math] И [math] z)[/math] ИЛИ [math](z [/math] И [math] x)[/math] | переключатель по большинству, 3-ППБ, мажоритарный клапан |
| [math]f_1[/math] | Разряд займа при тернарном вычитании | |
| [math]f_2[/math] | Разряд переноса при тернарном сложении | |
| [math]x+y+z[/math] | [math]+(x,y,z) = max(x,y,z) = (x\ OR\ y\ OR\ z) = OR(x,y,z) = (x [/math] ИЛИ [math] y [/math] ИЛИ [math] z) = [/math] ИЛИ [math](x,y,z)[/math] | 3-ИЛИ, максимум |
Представление функции формулой [ править ]
Тождественность и двойственность [ править ]
| Определение: |
| Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. |
Тождественность функций f и g можно записать, например, так:
[math]f(x_1, x_2, \dots, x_n)=g(x_1, x_2, \dots, x_n)[/math]
Просмотрев таблицы истинности булевых функций, легко получить такие тождества:
| [math]\overline<0>=1[/math] | [math]\overline<1>=0[/math] | [math]\overline<\overline | [math]x \land y=y \land x\![/math] | [math]x\lor y=y \lor x[/math] |
| [math]0 \land x=0\![/math] | [math]1 \land x=x\![/math] | [math]0 \lor x=x[/math] | [math]1\lor x=1[/math] | [math]x \land x=x \lor x=x[/math] |
А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:
| [math]x \land \overline | [math]x \lor \overline |
| [math]\overline | [math]\overline | (законы де Моргана) |
[math]x \land (y\lor z)=(x \land y)\lor (x \land z)[/math]
[math]x \lor (y \land z)=(x\lor y) \land (x\lor z)[/math] (дистрибутивность конъюнкции и дизъюнкции)
Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.
Суперпозиции [ править ]
| Определение: |
| Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных. |
Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.
Полнота системы, критерий Поста [ править ]
| Определение: |
| Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества. |
| Определение: |
| Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций. |
Американский математик Эмиль Пост [1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:
Представление булевых функций [ править ]
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ) [ править ]
| Определение: |
| Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов. |
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.
Конъюнктивная нормальная форма (КНФ) [ править ]
| Определение: |
| Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. |
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.
[math]f(x,y,z) = (x \lor y) \land (y \lor \neg
[math]f(x,y,z,t) = (x \lor t) \land (y \lor \neg
[math]f(x,y,z,t,m) = (x \lor m \lor \neg
Полином Жегалкина [ править ]
Полином Жегалкина имеет следующий вид:
[math]P = a_ <000\ldots000>\oplus a_ <100\ldots0>x_1 \oplus a_ <010\ldots0>x_2 \oplus \ldots \oplus a_ <00\ldots01>x_n \oplus a_ <110\ldots0>x_1 x_2 \oplus \ldots \oplus a_ <00\ldots011>x_
[math]f(x_1,x_2) = 1 \oplus x_1 \oplus x_1 x_2 [/math]
[math]f(x_1,x_2,x_3) = x_1 \oplus x_1 x_2 \oplus x_2 x_3 [/math]
[math]f(x_1,x_2,x_3,x_4) = 1 \oplus x_1 \oplus x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 x_2 x_4 [/math]
Тождественные функции. Выражение функций друг через друга [ править ]
| Определение: |
| Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения. |
Приведение тождественной функции есть выражение булевой функции через другие.
Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.
[math] x \oplus y = \left ( x \land \lnot y \right ) \lor \left ( \lnot x \land y \right ) = \left ( x \lor \lnot y \right ) \land \left ( \lnot x \lor y \right )[/math]
[math] x \downarrow y = \lnot \left ( x \lor y \right) = \lnot x \land \lnot y[/math]
[math]\langle x, y, z \rangle = \left ( x \land y \right ) \lor \left ( y \land z \right ) \lor \left ( x \land z \right ) = \left ( x \lor y \right ) \land \left ( y \lor z \right ) \land \left ( x \lor z \right )[/math]
Подстановка одной функции в другую [ править ]
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.
Отождествление переменных [ править ]
| Пример: |
| [math] f(a,b) = a \vee b [/math] — исходная функция [math] h(a) = a \vee a [/math] — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию [math]P_<1>[/math] — проектор единственного аргумента. |
Схемы из функциональных элементов [ править ]
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
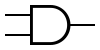 | 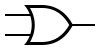 | 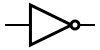 |  | 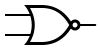 |
Стандартный базис [ править ]
[math] x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) [/math]
[math] x \rightarrow y = \lnot x \lor y [/math]
[math] 0 = x \land \lnot x [/math]
Функции [math] \mid \ и \downarrow[/math] являются отрицаниями функций [math] \land \ и \ \lor[/math] соответственно.
[math] x \mid y = \lnot \left ( x \land y \right )[/math]
[math] x \downarrow y = \lnot \left ( x \lor y \right )[/math]
Тождественность функций можно доказать с помощью таблицы истинности.
[math]x \leftarrow y = \lnot x \rightarrow \lnot y = x \lor \lnot y [/math]
Полнота стандартного базиса [ править ]
[math] x \land y = \lnot \left (\lnot x \lor \lnot y \right ) [/math]
[math] x \lor y = \lnot \left (\lnot x \land \lnot y \right ) [/math]
Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:
Теоремы о числе функций в базисе [ править ]
Значит, так как [math]X[/math] — безызбыточный базис, а система [math]\
Приведём примеры базисов для каждого [math]k[/math] :
[math]k = 1 \Rightarrow X = \< \downarrow \>[/math] ;
[math]k = 2 \Rightarrow X = \< \lnot, \land \>[/math] ;
Докажем, что последняя система является базисом: