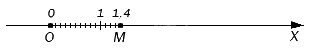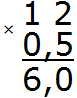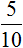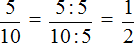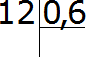для чего нужны десятичные дроби
Применение десятичной дроби в нашей жизни
Рассмотрим более подробно применение десятичных дробей в нашей жизни.
Дроби в медицине. В медицине, например, известно, что «великан» среди микробов имеет размер 0,1 мм, а наибольший мелкий вирус имеет размер 16 миллимикрон, т. е. (0,1: 1000 : 1000) х 16=0,0000016 (мм). Сравнивая размеры, медики определяют, чем вызвано заболевание (микробом или вирусом?), и узнают, какая болезнь». Дроби используются и в приготовление концентрированных растворов для жидких лекарств. Например, диагноз: закрытый перелом 1/3 (верхней) части голени. − Курс лечения: пить по 0,25 таблетки 3 раза в день, в течение 5 дней.
Дроби в кулинарии. В кулинарии (как и во всем поварском деле) все основывается на долях, на соотношениях. Стандартные рецепты приготовления видов хлеба (как пример) основываются на правилах долей.
В геодезии существует метод съемки земли, называемый космическое зондирование. Этот очень сложный метод можно упростить, используя дроби при расчетах формул. Благодаря им, геодезисты могут получить наиболее качественное изображение поверхности Земли. Дроби в космосе
Дроби в строительстве. Без знаний дробей невозможно построить здания, возвести мосты, проложить асфальт и т.д. Чтобы сделать строительный раствор необходимо знать дроби. Дроби используются в строительстве любого масштаба: для вычисления площадей и пропорций зданий, а также углов наклона стен и насыпей. Например, чтобы построить теплицу нужно измерить площадь земельного участка, толщину пленки. Оказывается, что и гвозди имеют размеры в десятичных дробях.
Дроби в рисовании. Для построения изображения головы человека высоту головы делим на 7 частей. Расстояние между глазами равно длине глаз. Ширина головы = 3\4 высоты головы
Дроби в фигурном катании. В фигурном катании десятичные дроби применяются при подсчете баллов для выявления победителей среди сильнейших фигуристов.
Дроби в музыке. В греческих сочинениях по математике дробей не встречалось. Греческие ученые считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам, механикам и другому «черному люду». Кроме арифметики и геометрии, в греческую науку входила музыка. Пифагорейцы, много занимавшихся музыкой и обожествлявшие число, считали, что Земля имеет форму шара и находится в центре Вселенной: ведь нет никаких оснований, чтобы она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и 5 планет (Меркурий, Венера, Марс, Юпитер и Сатурн) движутся вокруг Земли. Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат её из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал её при жизни. Его ученики – пифагорейцы, много занимавшиеся музыкой и обожествлявшие число, исследовали, насколько повышается тон струны, если её прижать посередине, или на четверть расстояния одного из концов, или на треть. Обнаружилось, что одновременное звучание двух струн приятно для слуха, если длины их относятся как 1:2, или 2:3, или 3:4, что соответствует музыкальным интервалам в октаву, квинту и кварту. Гармония оказалась тесно связанной с дробями, что подтверждало основную мысль пифагорейцев: «число правит миром»… Так дроби сыграли определяющую роль в музыке. И сейчас в общепринятой нотой записи длинная нота – целая – делится на половинки (вдвое короче), четверти, восьмые, шестнадцатые и тридцать вторые. Таким образом, ритмический рисунок любого музыкального произведения, созданного европейской культурой, каким бы сложным он ни был, определяется десятичными дробями.
Практическая часть
В качестве примера применения десятичных дробей в нашей жизни, я решил подготовить математическую игру для одноклассников. Я придумал несколько заданий. Которые можно использовать как на уроке, так и на внеклассном занятии. Данную игру я провел среди учащихся 5″а» класса, и вот какие отзывы я получил от них.
Афанасьев А.-Игра мне очень понравилась, заданий было много и все разнообразные.
Тарасов Е.- Игра была увлекательная и интересная.
Калинин Д.- Мне понравилась игра там было много интересных заданий.
Шамшина Д.- Игра помогла мне закрепить знания которые прошли на уроке.
Задачи
1.Сбербанк начисляет вкладчику 12 % годовых. Вкладчик положил на счет 30 000 руб. и не снимал деньги со счета в течение трех лет и не брал процентные начисления. Сколько денег будет на счете вкладчика через год? Через три года?
2.Холодильник стоил 12 600 руб. В мае цена холодильника была снижена на 20%, а в июне – еще на 5%. Какой стала стоимость холодильника в июне?
3.В начале года тариф на электроэнергию составлял 4,2 р. за 1кВт/ч. В середине года он увеличился на 10%, а в конце года еще на 4%. Каков тариф стал после повышения?4.Длина прямоугольного участка составляет 19,4 метра, а ширина на 2,8 метра меньше. Вычислите периметр участка.
5. В швейной мастерской было 5 цветов ленты. Красной ленты было больше, чем синей на 2,4 метра, но меньше, чем зеленой на 3,8 метра. Белой ленты было больше, чем черной на 1,5 метра, но меньше, чем зеленой на 1,9 метра. Сколько метров ленты всего было в мастерской, если белой было 7,3 метра?
Вопросы
Укажите верную запись десятичной дроби «три целых пять сотых»
Вопрос № 2
В каком разряде числа 6,0359 записана цифра 5?
сотых
тысячных
тысяч
десятых
Вопрос № 3
Запишите дробь 21,0100 короче.
Вопрос № 4
Между какими соседними натуральными числами находиться число 3,19?
3,1 и 3,2
3 и 19
3 и 5
3 и 4
Задание №3
В каком примере допущена ошибка? Объяснить.
А) 3,7 + 1,2 = 4,9 Б) 7,34 + 10,1 = 17,35
В) 4,2 – 2,03 = 2,17 Г) 8,95 – 0,6 = 8,89
Задание №4
Впишите знаки действий:
а) 8,8 * 10 = 88; б) 3,3 : 100 = 0,033; в) 7,5 * 100 = 750.
Задание №5
Запишите пропущенное число:
А) 42, 3 * 10 = 423; б) 0,05 * 100 = 50; в) 3800 * 10 = 380.
Заключение.
Изучив в 5 классе тему «Десятичные дроби», мне захотелось узнать больше, чем написано в учебнике.
Поэтому рассмотрев многие учебники по математике, подобрав необходимый материал в интернете, я ответил на цели и задачи, поставленные ранее, а именно:
· Рассмотрел историю возникновения дробей. Узнал великих математиков, которые внесли новое в определение «десятичная дробь».
· Сформировали умения производить вычисления с десятичными дробями, необходимые для применения в практической деятельности;
Работая над темой данного проекта, по-моему мнению, необходимо было подобрать ряд задач по данной тематике. Такие задачи, которые интересны будут не только для меня, но и для обучающихся 5 классов. Познавательный материал способствует, по- моему мнению, не только выработке умений и закреплению навыков вычислений, но и формирует устойчивый интерес к процессу и содержанию деятельности, а также познавательной и социальной активности. В данной работе я старался показать, что дробь – это постоянный спутник нашей жизни.
Проект на тему «Десятичные дроби в нашей жизни»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Проект по математике. Тема: «Десятичные дроби в нашей жизни». Выполнила: Ученица 5Б класса МБОУ «Школы №15» Анохина Диана. Под руководством: Смирновой Ирины Александровны
Цель ответить на вопрос: Как и где используются десятичные дроби в современной жизни? А как?
Задачи Провести опрос Проанализировать литературу по данной теме изучить профессии, в которых используются десятичные дроби подобрать и решить задачи с практическим содержанием
Как вы думаете нужны ли десятичные дроби?
Используются ли десятичные дроби в жизни? В больницах – 8,6 %; в магазинах – 17,4%; На математике – 17,4% ; В работе – 4,3 %; В жизни – 13,1% ; На заводах – 4,3% ; На кухне – 4,3% ; В учёбе – 17,4% ; На работе – 8,6% ; В разн. Профессиях – 4,3%
Выводы по опросу одноклассники знают, что десятичные дроби нужны в жизни. Но почти 50% класса не знают, где они применяются
Где применяют десятичные дроби? Десятичные дроби применяют: •на кухне •в налогах •в кредитовании •в подсчетах голосов на выборах •на почте •в бухгалтерии и т.д.
Применение десятичных дробей в заработной платы: Расчет заработной платы
Применение десятичных дробей в медицине: 1) Применение количества (дозы) лекарства 2) Поставить больному капельницу 3) Сделать инъекцию
Задача № 2. В самолёт для полярной экспедиции загрузили 3 трактора, массой 1,2 т. каждый, и 7 аэросаней. Масса всех аэросаней на 2 т. больше массы тракторов. Какова масса одних аэросаней? 1)1,2 * 3=3,6(т)-масса 3-ёх тракторов. 2)3,6 + 2=5,6(т)-масса 7-ми аэросаней. 3)5,6 / 7=0,8(т) Ответ: 0,8 т. масса одних аэросаней.
Все лентяи говорят « Математика сложна!» Отвечаем вам, друзья: Без математики нельзя.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-693917
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям
Время чтения: 2 минуты
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В МГПУ сформулировали новые принципы повышения квалификации
Время чтения: 4 минуты
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Десятичные дроби: определения, запись, примеры, действия с десятичными дробями
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Десятичные дроби представляют собой дробные числа в десятичной записи.
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Что такое разряды в десятичных дробях
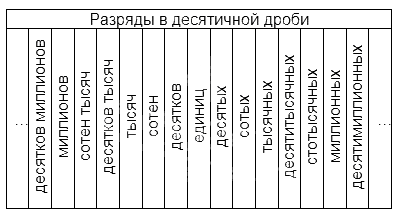
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Положение десятичных дробей на оси координат
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Применение десятичных дробей
Десятичные дроби имеют широкий спектр применения. Их применяют в экономике, медицине, машиностроении и во многих других отраслях. В данном уроке мы рассмотрим некоторые элементарные операции, которые могут пригодиться в будущем.
Сравнение десятичных дробей
Чтобы сравнить две десятичные дроби, нужно в обеих дробях сделать количество цифр после запятой одинаковым, приписáв к одной из них нули. Затем отбросить запятые в обеих дробях и сравнить получившиеся числа.
Значит и дробь 5,345 меньше, чем дробь 5,36
Пример 2. Сравнить десятичные дроби 6,782 и 6,71
Сделаем количество цифр в обеих дробях одинаковым:
6782 больше, чем 6710
Значит и дробь 6,782 больше, чем дробь 6,71
Нахождение десятичной дроби от числа
В прошлых уроках мы находили обыкновенную дробь от числа. Для этого мы делили число на знаменатель дроби и полученный результат умножáли на числитель дроби.
Например, чтобы найти от числа 9, нужно число 9 разделить на знаменатель дроби и полученный результат умножить на числитель этой же дроби
Значит от числа 9 составляет 6.
Но находить можно и десятичные дроби от числа. Нахождение десятичной дроби от числа намного проще. Чтобы найти десятичную дробь от числа, достаточно это число умножить на данную дробь.
Например, найдём 0,5 от числа 12. Чтобы найти 0,5 от числа 12, достаточно умножить 12 на 0,5
Получили ответ 6. Значит 0,5 от числа 12 составляет число 6.
Проверим правильно ли мы нашли 0,5 от числа 12. Сначала переведём десятичную дробь 0,5 в обыкновенную дробь. 0,5 это ноль целых и пять десятых. Ноль не пишем, а записываем сразу пять десятых:
Cделаем эту дробь более простой для нашей работы. Для этого сократим её на 5
Получили дробь 


Пример 2. Найти 0,4 от одного метра
Один метр это 100 см. Чтобы найти 0,4 от 100 см, нужно 100 см умножить на 0,4. А чтобы умножить 100 см на 0,4 нужно в 0,4 перенести запятую вправо на две цифры:
Значит 0,4 от одного метра составляют 40 см.
Десятичную дробь также можно найти от десятичной дроби. Например, найдем 0,5 от 2,5. Для этого 2,5 нужно умножить на 0,5
Нахождение числа по десятичной дроби
В прошлых уроках мы находили число по обыкновенной дроби. Чтобы найти всё число по его дроби мы делили известное число на числитель дроби и полученный результат умножали на знаменатель дроби.
Например, если 
Значит если всё число равно 12.
Находить число можно и по десятичной дроби. Нахождение числа по десятичной дроби намного проще. Чтобы найти число по десятичной дроби, достаточно это число разделить на данную дробь.
Пример 1. 0,6 всего числа составляет 12, найти всё число. Чтобы найти всё число, достаточно 12 разделить на 0,6.
Чтобы разделить 12 на 0,6 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 120 : 6. А это выражение вычисляется легко:
Значит, если 0,6 всего числа составляет 12, то всё число это 20.
Пример 2. Велосипедист проехал 3 км, что составляет 0,2 всего пути, который должен проехать велосипедист. Какой путь должен проехать велосипедист?
Если 0,2 всего пути составляют 3 км, то для того чтобы найти весь путь, нужно 3 разделить на 0,2. Чтобы разделить число 3 на 0,2 нужно в делимом и в делителе перенести запятую вправо на одну цифру. Тогда получим выражение 30 : 2. А это выражение вычисляется легко:
Значит весь путь, который должен проехать велосипедист составляет 15 км.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
19 thoughts on “Применение десятичных дробей”
Спасибо владельцам ресурса за их труды! У меня проблемы с математикой) искал где учить, что бы было коротко и по делу и вот нашел ваш сайт. Радует чистый дизайн, который не отвлекает и типографика отличная
Огромное спасибо обладателю этого ресурса. Прекрасные уроки!
Было бы хорошо, если важные моменты выделяли в специальное обведенное поле, как правило, теорема или просто подсказка. Иногда читать одно и тоже по нескольку раз за статью очень отвлекает и начинаешь путаться, так как думаешь, что это разные правила
Здравствуйте. Спасибо за разумную критику. Уже думали над этим и хотим отказаться от такого формата. Причина по которой правило повторяется по нескольку раз за урок — чтобы человек понял, как его применять на практике. С первого раза мало кому удается «въехать».
помогите я запуталась. Сначало написано, что находя число от дроби, нужно умножить разделить на знаменатель, затем умножить на числитель, потом наоборот. Или я не понимаю.
Если находите обыкновенную дробь от числа, то делите число на знаменатель дроби и полученный результат умножаете на числитель.
Если находите десятичную дробь от числа, то просто умножаете это число на десятичную дробь.
Не меняйте ничего. Повторение очень помогает умвоению материала. Без этого вся информация улетучивпется очень быстро. Все идеально сделано. Это в первый раз когда я в е понимаю до мелочей и во ного благодаря повторению