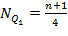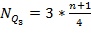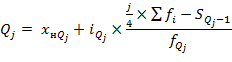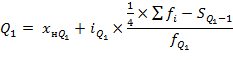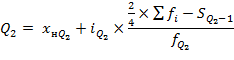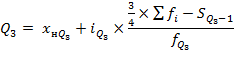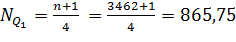для чего нужны квартили
Для чего нужны квартили
Предоставляют важную информацию о структуре вариационного ряда к-л признака. Вместе с медианой они делят вариационный ряд на 4 равные части. Квартилей две, их обозначают символами Q, верхняя и нижняя квартиль. 25% значений меньше, чем нижняя квартиль, 75% значений меньше, чем верхняя квартиль.
Для расчёта квартили надо поделить вариационный ряд медианой на две равные части, а затем в каждой из них найти медиану. К примеру, если выборка состоит из 6 элементов, тогда за начальную квартиль выборки принимается второй элемент, а за нижнюю квартиль пятый элемент.
В случае, если вариационный ряд состоит к примеру, из 9 элементов, тогда за верхнюю квартиль принимают арифм. среднее 2-го и 3-го элеметов, а за нижнюю арифм. среднее 7-го и 8-го элементов.
Пример 1
Две стат. совокупности имеют след. частотные таблицы:
Для обеих совокупностей кол-во членов 28, арифм. среднее 10, медиана 10. Но у первой совокупности значения признака более плотно расположены около арифм. среднего, а у второй более редко. В первом случае значения признака имеют меньшее рассеяние, а во втором большее. Но рассмотренные до сих пор характеристики этого не показывают Одно или несколько ненормально больших или малых значений признака могут существенно увеличить протяжённость области значений признака, то от начала и конца вариационного ряда отбрасывают некоторые члены. Это и происходит с помощью квартилей.
В нашем примере для первой совокупности нижняя квартиль 9, верхняя 11 (отличие равно 2)
Для второй совокупности ниняя квартиль 8, верхняя 12 (отличие равно 4), так как в обеих совокупностях надо отбросить по четверти, то есть по 7 членов от обоих концов ряда.
Видим, что у второй совокупности рассеяние больше, чем у первой.
Пример 2
Фирма по продаже сувениров желает узнать рабочую выработку. В данном списке представлено количество сувениров, сделанных каждым рабочим за какой-то день:
92, 100, 89, 98, 101, 84, 113, 93, 81, 14, 113, 86, 98, 99, 105, 88, 101, 89, 93, 102, 101, 99, 87, 109, 92, 99, 111, 98, 102, 95
Найдём верхнюю и нижнюю квартили. В вариационном ряду 30 значений: 14, 81 84, 86, 87, 88, 89, 89, 92, 92, 93, 93, 95, 98, 98, 98, 99, 99, 99, 100, 101, 101, 101, 102, 102, 105, 109, 111, 113, 113.
Б) Квартили



Квартили представляют собой значения признака, делящие упорядоченную по возрастанию совокупность на четыре равные по количеству элементов части.
Различают квартиль первого порядка (нижний квартиль) 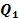
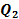
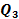
Для расчёта квартилей можно поделить вариационный ряд медианой на две равные части, а затем в каждой из них найти медиану.
К примеру, если выборка состоит из 6 элементов, тогда за начальную квартиль выборки принимается второй элемент, а за нижнюю квартиль пятый элемент.
1 квар 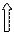 тиль тиль | 2 квартиль |
В случае, если вариационный ряд состоит к примеру, из 9 элементов, тогда за верхнюю квартиль принимают арифметическое среднее 2-го и 3-го элементов, а за нижнюю арифметическое среднее 7-го и 8-го элементов.
Расчет квартилей для дискретного ряда:
1. В дискретном ряду сначала определяют номера квартилей :
номер 1-го квартиля
позиция 3-го квартиля
2. Если номер квартиля – целое число, то значение квартиля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру квартиля. Например, номер квартиля равен 20, его значение будет равно значению признака с S =20 (накопленной частотой равной 20).
Если номер квартиля – нецелое число, то квартилем будет условное число между двумя наблюдениями. Значением квартиля будет сумма, состоящая из значения элемента, для которого накопленная частота равна целому значению номера квартиля, и указанной части (нецелая часть номера квартиля) разности между значением этого элемента и значением следующего элемента.
Например, если номер квартиля равна 20,25, квартиль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 (0,25) разности между значением 20-го и 21-го наблюдений.
Пример. Найти третий квартиль
Заработная плата рабочего, тыс.руб; 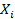 | бригада 1 | бригада 2 | |
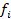 , число рабочих , число рабочих | 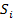 , накопленная частота , накопленная частота | 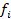 , число рабочих , число рабочих | 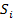 , накопленная частота , накопленная частота |
  18 18 | |||
 20 20 | |||
| Итого: |
1) Определяем номер 3-го квартиля
для первой бригады 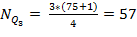
для второй бригады 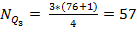
2) Для первой бригады номер квартиля – целое число. Следовательно, нужно найти элемент совокупности, для которого накопленная частота S равна номеру квартиля. Для этого определяем самую первую накопленную частоту, которая больше или равна номеру квартиля. Это накопленная частота второго значения признака Хi=18, Si=57.
Определяем значение третьего квартиля для первой бригады :Q3 = x57 = 18 тыс.руб.
Это значит, что заработная плата 75% рабочих 1-ой бригады менее 18 тыс.руб
Определяем их значение с помощью самой первой накопленной частоты большей или равной порядковым номерам элементов (57 и 58). Х57= 18, х58= 20.
Теперь определяем значение 3-го квартиля для второй бригады:
Это значит, что заработная плата 75% рабочих второй бригады менее 19,5 тыс.руб.
Расчет квартилей для интервального ряда:
Для расчета квартилей для интервального ряда
1. Определяем номер квартиля по тем же формулам, что и для дискретного ряда,
2. Определяем квартильный интервал по накопленной частоте. Это первый интервал, для которого накопленная частота будет больше или равна номеру квартиля.
3. Рассчитываем квартиль по формуле:
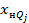
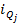
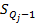
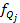
Пример. Найти первый квартиль для интервального ряда.
| Возрастные группы | Число студентовf | Накопленная частота S |
| До 20 лет | ||
| 20 — 25 | ||
| 25 — 30 | ||
| 30 — 35 | ||
| 35 — 40 | ||
| 40 — 45 | ||
| 45 лет и более | ||
| Итого |
1. Определяем номер первого квартиля по формуле
2. Первый квартиль находится в возрастной группе 20-25 лет, так как это первый интервал, для которого накопленная частота больше (или равна) номера квартиля (346 865,75).
3. Определяем первый квартиль по формуле
4.
Это значит, что четверть студентов младше 22,98 лет.
Квартиль
Опубликовано 16.06.2021 · Обновлено 17.06.2021
Что такое Квартиль?
Квартиль – это статистический термин, который описывает разделение наблюдений на четыре определенных интервала на основе значений данных и их сравнения со всем набором наблюдений.
Общие сведения о квартилях
Медиана является надежным средством оценки местоположения, но ничего не говорит о том, как данные по обе стороны от ее значения распространяются или рассредоточены. Вот где вступает в игру квартиль. Квартиль измеряет разброс значений выше и ниже среднего путем деления распределения на четыре группы.
Ключевые моменты
Как работают квартили
Точно так же, как медиана делит данные пополам, так что 50% измерения лежит ниже медианы, а 50% – выше нее, квартиль разбивает данные на кварталы, так что 25% измерений меньше нижнего квартиля, 50 % меньше среднего, а 75% меньше верхнего квартиля.
Квартиль делит данные на три точки – нижний квартиль, медиана и верхний квартиль – для формирования четырех групп набора данных. Нижний квартиль или первый квартиль обозначается как Q1 и является средним числом, которое находится между наименьшим значением набора данных и медианой. Второй квартиль, Q2, также является медианным. Верхний или третий квартиль, обозначаемый Q3, является центральной точкой, которая находится между медианой и наивысшим номером распределения.
Теперь мы можем выделить четыре группы, сформированные из квартилей. Первая группа значений содержит наименьшее число до Q1; во вторую группу входит Q1 до медианы; третий набор – это медиана Q3; четвертая категория включает Q3 в самую высокую точку данных всего набора.
Каждый квартиль содержит 25% от общего числа наблюдений. Как правило, данные располагаются от наименьшего к наибольшему:
Пример квартиля
Предположим, что баллы по математике в классе из 19 учеников в порядке возрастания распределены следующим образом:
59, 60, 65, 65, 68, 69, 70, 72, 75, 75, 76, 77, 81, 82, 84, 87, 90, 95, 98
Сначала отметьте медианное значение Q2, которое в данном случае является 10- м значением: 75.
Q1 – это центральная точка между наименьшей оценкой и медианой. В этом случае Q1 попадает между первым и пятым баллом: 68. [Обратите внимание, что медиана также может быть включена при вычислении Q1 или Q3 для нечетного набора значений. Если бы мы включили медианное значение по обе стороны от средней точки, то Q1 будет средним значением между первым и 10- м баллами, что является средним значением пятого и шестого баллов – (пятый + шестой) / 2 = ( 68 + 69) / 2 = 68,5].
Q3 – это среднее значение между Q2 и наивысшим баллом: 84. [Или, если вы включаете медиану, Q3 = (82 + 84) / 2 = 83].
Теперь, когда у нас есть квартили, давайте интерпретируем их числа. Оценка 68 (Q1) представляет первый квартиль и 25- й процентиль. 68 – это медиана нижней половины оценки, установленной в имеющихся данных, то есть медиана оценок от 59 до 75.
Q1 говорит нам, что 25% оценок ниже 68 и 75% оценок класса выше. Q2 (медиана) – это 50- й процентиль и показывает, что 50% оценок меньше 75, а 50% оценок выше 75. Наконец, Q3, 75- й процентиль, показывает, что 25% оценок являются больше и 75% меньше 84.
Особые соображения
Если точка данных для Q1 дальше от медианы, чем Q3 от медианы, то мы можем сказать, что существует больший разброс среди меньших значений набора данных, чем среди больших значений. Та же самая логика применяется, если Q3 дальше от Q2, чем Q1 от медианы.
В качестве альтернативы, если имеется четное количество точек данных, медиана будет средним из двух средних чисел. В нашем примере выше, если бы у нас было 20 студентов вместо 19, медиана их оценок будет средним арифметическим 10- го и 11- го числа.
Квартили используются для расчета межквартильного размаха, который является мерой изменчивости вокруг медианы. Межквартильный размах просто рассчитывается как разница между первым и третьим квартилями: Q3 – Q1. Фактически, это диапазон средней половины данных, который показывает, насколько разбросаны данные.
Для больших наборов данных в Microsoft Excel есть функция КВАРТИЛЬ для вычисления квартилей.
Квартиль 2021
Table of Contents:
Что такое «квартиль»
Старайтесь не путать четверть с квартикой.
BREAKING DOWN ‘Quartile’
В то время как медиана является надежной оценкой местоположения, она ничего не говорит о том, как данные по обе стороны от ее значения распространяются или распределяются. Квартал измеряет распространение значений выше и ниже среднего, разделив распределение на четыре группы. Точно так же, как медиана делит данные на половину, так что 50% измерения лежит ниже медианы и 50% лежит над ней, квартиль разбивает данные на четверти, так что 25% измерения меньше, чем нижняя квартиль, 50 % меньше среднего, а 75% меньше, чем верхний квартиль.
Каждый квартиль содержит 25% от общего количества наблюдений. Как правило, данные распределяются от самых маленьких до крупнейших, причем эти наблюдения падают ниже 25% от всех проанализированных данных, выделенных в 1-м квартиле, наблюдения падают между 25. 1% и 50% и распределяются во 2-м квартиле, тогда наблюдения падают между 51% и 75% выделены в 3-м квартиле и, наконец, остальные наблюдения, выделенные в 4-м квартиле.
Пример квартили
Давайте работать с примером.Предположим, что распределение математических баллов в классе из 19 учеников в порядке возрастания:
Если существует четное количество точек данных, медиана будет средним числом средних двух чисел. В нашем примере выше, если бы у нас было 20 учеников вместо 19, медиана их баллов будет средним арифметическим для десятого и одиннадцатого чисел.
Для больших наборов данных Microsoft Excel может использоваться для вычисления квартилей с помощью функции QUARTILE.
Для чего нужны квартили
Ниже мы рассмотрим некоторые общие приложения квантилей.
Анализ непрерывных переменных. Непрерывные переменные, например концентрацию холестерола или дыхательный объем легких, в статистических исследованиях часто также делят на несколько диапазонов. Для этой цели обычно используют квантили, чтобы во всех группах было равное число измерений. При такой группировке часть информации теряется, но появляется возможность представить данные в более простом виде, например, в виде таблиц. Чем меньше групп, тем больше информации теряется. В регрессионном анализе непрерывные независимые переменные иногда делят по амплитуде на две или более групп. Это слегка усложняет анализ, но позволяет избежать предположения о линейном соотношении между двумя анализируемыми величинами. Однако, такой подход ведет к модели, в которой вероятность изменяется скачками при некоторых значениях переменной, а не равномерно увеличивается.
Вычисление квантилей. Вычисление центилей и других квантилей не настолько просто, как может показаться. Данные должны быть упорядочены от 1 до n в порядке возрастания. K й центиль получается вычислением величины q=k*(n+1)/100 и ее последующей интерполяцией между двумя ближайшими к q значениями данных (бо’льшим и меньшим). Например, для 5 ого центиля выборки из 145 наблюдений мы имеем q=5*146/100=7/3. Таким образом, 5-ый центиль находится на 3/10 расстояния от 7 го к 8 му упорядоченному наблюдениям. Если значения этих данных равны 11.4 и 14.9 соответственно, то искомый центиль равен 12.45. Доверительные интервалы могут быть построены для любого квантиля. 3