для чего нужны сплайны
Не «поликами» едиными…
Не «поликами» едиными…
Часть 1: Моделирование при помощи сплайнов.
Доброго времени суток! Меня зовут Александр Савич, живу в г. Винница. С 3d познакомился несколько лет назад. Всё это время изучаю пакет 3d Studio Max.
Для начала давайте, создадим раму тренажёра, думаю, сложного в этом ничего нет, обыкновенные chamferbox. Поэтому не буду на этом останавливаться, перехожу к деталям, первой которую мы рассмотрим, будет рукоятка винта для регулировки положения сиденья.
Внутри Ngon создаём ещё одну фигуру Circle и выравниваем её по центру фигуры Ngon01. Эти фигуры, а так же другие вы найдёте в панели Create, в разделе Shapes(фигуры) (рис 3).
Выделяем наш Ngon01,зажимаем шифт и с помощью инструмента тянем немного вперёд, тем самым клонируя фигуру, в появившемся окне выбираем Copy,жмём ОК. то же самое проделываем с Circle01.размещаем фигуры как на рис. 4.
Выделяем Ngon01,кликаем правой кнопочкой мыши на нём и конвертируем в редактируемый сплайн. Convert to editable spline. Переходим на панель Modify, в свитке.
Geometry,активируем кнопку Attach и поочёрёдно кликаем на все фигуры (сплайны). В свитке Selection,выберите spline или нажмите на клавиатуре цифру 3.Выделите все фигуры-сплайны что на рис 5, они все станут красными во вьюпорте.В свитке Geometry активируйте кнопку Outline и справа от кнопки покрутите (введите) нужное число,что бы получилось примерно как на рис 5.
Примечание: Зачем нужен Outline? Это как Chamfer в Edit Poly, в данном случае можно обойтись и без него, но при моделировании сложных моделей без этого не обойтись, так как могут появиться артефакты при работе с сурфейс модификатором, поэтому прикинув немного, решил показать на простом примере.
Таким образом мы соеденили вершины. Ищем в стеке модификаторов Surface модификатор и применяем его.Наш каркас обрёл поверхность. При необходимости в настройках Surface активируем flip normals, выставляем Steps(шаг) 20 вполне достаточно,это как с интерациями в edit poly,чем больше шаг тем больше полигонов.
С винтом закончили. По тому же принципу делаем гайку (рис 08).
Создаём Ngon с 6 сторонами, и ещё один поменьше (рис 8 номер 3, помечен жёлтым.) с включенным параметром Circular (рис 9) Дело в том что в каждом сплайне должно быть одинаковое ко-во вершин для корректной работы с Cross section.
И снова Cross section.
Начиная с 4-го сплайна, после удаляем 6-й сплайн, выделяем вершины, и снова Fuse.
Дело за Surface модификатором, применяем, ставим Steps: 6.
Вот и закрепили пройденный материал.
Часть 2: Сплайны и модификатор Bevel-Profile.
Выделяем все вершины и делаем их corner (правый клик на вершине, контекстное меню (рис 11)).Оставляем выделенными все вершины, активируем кнопку Fillet (фаска), напротив кнопки в счётчик вводим небольшое значение, видим как закругляются углы (Рис 13).
Выделяем нашу сплайн-форму и применяем модификатор Bevel-Profile, нажимаем на кнопку модификатора Pick Profile и указываем наш сплайн- путь, вот собственно и всё.
Часть 3: Сплайны и привязка к вершине.
На этот раз мы смоделируем такой вот корпус (рис15).
Для этого создаём в проэкции front, фигуру Rectangle и конвертируем её в редактируемый сплайн,убедитесь что тип вершин corner, немного переместите нижние вершины на встречу друг другу. Выделив все вершины применяем fillet,подкручиваем счётчик, с помощью инструмента с зажатым шифтом, копируем наш сплайн несколько раз и правим вершины, в центре рисуем circle. Выделенные сплайны выдвигаем немного вперёд по оси Y (рис 16).
С помощью кнопки Refine(рис17)впихиваем новые вершины в наши сплайны (рис18).
Включаем привязку Vertex, нажав левой кн.,чтобы активировать,а потом пр. кн.мыши на кнопку Snaps toggle (Рис19).
С включенной привязкой, активируем кнопку Create Line,находящуюся в свитке Geometry. Активируйте подобъект Vertex,если он у вас ещё не активирован,чтобы видеть наши вершины во вьюпорте, и начинайте соединять наши вершины, привязка нам в этом поможет. Вот что должно получиться (Рис 20).
Теперь копируем выделенный на (рис 21) сплайн,перемещаем его немного назад и присоединяем его к остальным с помощью Cross section.
Итак, каркас нашей детали готов, осталось применить Surface,после чего в стеке модификаторов выбираем Shell, и задаём толщину нашей модели в поле Inner Amount, в Outer amount оставить 0.Затем нашу половинку нужно «отзеркалить» с помощью функции Mirror по оси Y,в качестве Clone selection выбрать Copy.
Часть 4: Сплайны и модификатор Lathe(вращение)
Что бы получить такую фигуру как на (рис22).достаточно создать сплайн и применить модификатор Lathe.
Настройки модификатора вращения просты в освоении.
Вкратце: weld Core соединяет вершины в центре оси вращения. Flip Normals разворачивает нормали, прежде всего назначьте модели двухсторонний материал, проще будет ориентироваться. В поле Direction выбираете ось, по которой будет происходить вращение. В панели Align производится выравнивание по центру, минимуму и максимуму. Если возникли проблемы с вращением можно подвигать контейнер оси, для этого раскрываете плюсик слева от названия модификатора, активируете Axis и двигаете во вьпорте.
Часть 5: Подводим итоги.
Путеводитель по полиномам и сплайнам для программиста
Итак, вы программист. Зачем вам вообще могут понадобится полиномы? Например затем, что это хорошая геометрическая глина, из которой можно слепить разные вещи.
Из нашей статьи, объясняющей сущность математического анализа на примере python’а, крови и динамита, видно, что вы можете анализировать и синтезировать произвольные функции в качестве многочленов. Однако вовсе не обязательно работать именно с функциями. Иногда вам может понадобиться смоделировать сплайн из нескольких точек или свойств, вроде тангенсов кривых. Например, вам надо слепить какую-нибудь анимацию, или приятный видео эффект, или провести кривую, проходящую через определенные точки, или создать поверхность плоскую в одном месте и изогнутую в другом.
Многочлены, в том числе даже сплайновые, могут далеко не всегда оказаться лучшим инструментом для этой задачи, однако они обладают некоторыми чертами, которые программисты очень ценят. Они просты и универсальны по своей природе, а также, что особенно важно, очень эффективны с точки зрения производительности. Возьмем, например следующий полином:
Для его вычисления требуется всего 6 действий умножения и 3 сложения. Это важно, поскольку ваша модель будет постоянно подвергаться вычислениям. Но и здесь мы можем произвести оптимизацию. В этом нам поможет схема Горнера. С ее помощью тот же самый многочлен можно записать в виде
А это уже всего 3 умножения и 3 сложения. Вот видите, мы только начали, а вы уже научились избавляться от одной трети вычислений.
Полиномиальная интерполяция
Задача адаптации многолчена n-ной степени под n+1 точку пространства называется полиномиальной интерполяцией. Существует несколько способов ее реализации. Вы можете воспользоваться интерполяционными формулами Ньютона или Лагранжа, однако самый простой способ получения интерполяционного многочлена — решение системы линейных уравнений.
Если многочлен проходит через точку, значит, мы, очевидно, можем утверждать, что P(xi) = yi. Допустим, мы хотим адаптировать полином под набор из трех точек. Это означает, что:
В общем случае, мы не можем провести прямую через три произвольные точки. И потому нам придется искривить ее, сформировав параболу. Или, иными словами, ввести многочлен второй степени, также известный как квадратичная функция.
Поскольку xs и ys известны, нам остается только решить систему и узнать коэффициенты a, b, c, и поскольку эта система из трех уравнений и трех переменных, мы как правило можем получить одно единственное решение.
Чтобы убедиться в этом попробуйте переместить положение трех точек на нижнем графике и посмотрите, что произойдет.
Этот график также очень полезен для мысленного анализа линейных систем. В общем случае, уместить прямую линию в трех точках нельзя, равно как и нельзя найти решение для системы из n уравнений при n-1 неизвестных переменных. Но иногда это возможно. Например, в случаях, когда некоторые из точек совпадают или все они намерено расположены на одной прямой.
Обратная ситуация еще интереснее. Мы можем провести бесконечное количество парабол через две заданные точки. Все они одинаково подходят в качестве решения задачи. И в то же время мы не можем получить некое однозначно лучшее решение для систем из n уравнений и n+1 переменных.
Но что если это все-таки возможно? Что если мы можем ввести некоторый дополнительный критерий для выбора наиболее подходящего варианта?
Синтез
Подобные вопросы ведут нас на территорию полиномиального синтеза. В нашем случает это нечто среднее между полиномиальными рядами и полиномиальной интерполяцией. С помощью рядов мы можем смоделировать функцию на основе ее производных в некоторой точке, а с помощью синтеза — воспользоваться как точками, так и производными (и не только ими, но об этом в другой раз).
Производная функции тесно связана с геометрическими свойствами ее графика. Первая производная определяет тангенс угла наклона касательной, а вторая — кривизну.
Допустим нам необходимо определить функцию, проходящую через две точки, зная ее тангенс в обоих точках. В таком случае мы можем легко синтезировать ее в виде многочлена.
Как и ранее, нам понадобится записать систему уравнений. Теперь нам нужны четыре условия, поэтому нам следует выбрать многочлен 3 степени, то есть кубическую функцию.
Некоторые из уравнения сформированы на основе точек, а другие — производных. Сюда также можно добавлять и интегралы для введения необходимых свойств целочисленности, что делает эту технику довольно эффективной.
Но мы продолжим рассматривать функцию, соединяющую две точки непрерывной плавной прямой с тангенциальными ограничениям в этих точках.
Феномен Рунге
У полиномиальной интерполяции есть неприятное свойство, проявляющееся в увеличении роста осцилляций на обоих концах интервала с ростом количества точек. Это явление получило название феномен Рунге. Он ограничивает возможности применения простых полиномиальных интерполяций.
Другой недостаток этого подхода — его глобальность, то есть изменение всей функции вместе с малейшим изменением положения хотя бы одной точки. В сочетании с осцилляциями получается самый что ни есть хаос.
Узлы Чебышева
Один из способов борьбы с хаосом заключается в выборе специальной сетки для интерполяции — узлов Чебышева. Это специальные значения x, которые получаются путем деления полукруга с радиусом 1 на равные фрагменты и их проецирования на ось x.
Вообще, в этом приеме кроется определенное математическое волшебство, но с прагматической точки зрения, он предназначен для минимизации феномена Рунге. И хотя он не позволяет сделать интерполяцию совершенно предсказуемой, на отрезке (-1:1) все работает стабильно.
Конечно, вы можете расширить интервал по оси X настолько, насколько нужно с помощью одномерного аффинного преобразования. Не обязательно придерживаться отрезка (-1; 1).
Но интерполяция при этом сохраняет свою повсеместность. Изменение первой точки по-прежнему влияет на работу функции возле последней, хотя и не настолько существенно.
Сплайны
Существует довольно много разновидностей сплайнов, но всех их объединяет один сценарий применения. Как только глобальная интерполяция по какой-либо причине перестает годиться для наших задач, мы можем разделить наш интервал на более малые фрагменты и определить отдельные функции для интерполяции на каждом из них.
Единственное, что нам нужно учесть, так это необходимость их соединения на концах для сохранения непрерывности. Если мы гарантируем непрерывность не только итоговой, кусочно-заданной функции, но и ее первой производной, то в таком случае тангенсы каждого ее отрезка будут совпадать, а ее график будет выглядеть плавно.
Существует определенная классификация сплайнов. Например, возьмем полиномиальный сплайн, состоящий из двух фрагментов. Если каждый его фрагмент определяется полиномом третьей степени, то он называется кубическим. Он может обладать, например, таким свойством, как непрерывность первой производной, поскольку тангенсы на стыке фрагментов совпадают. Его фрагменты имеют не равную ширину. Он не естественного происхождения, поскольку мы можем управлять производными на его концах. И конечно же это интерполяционный сплайн, поскольку он проходит точно через указанные нами точки сетки.
Заключение
Вероятность того, что вам когда-либо придется реализовывать на практике собственную интерполяцию крайне мала. Существует много готовых решений и в большинстве случаев вам надо будет просто выбрать правильный инструмент для работы. Эта область знаний не так сложна, но количество неизвестных слов и названий может оттолкнуть.
Целью этого путеводителя было предоставить вам базовое понимание идей, используемых для работы с полиномами и сплайнами. Он ни в коем случае не претендует на полноту изложения, ведь на самом деле, по каждой из небольших глав этого материала написаны целые книги. Но мы надеемся, по крайней мере, что интерактивный подход к изложению в этом материале будет полезен не только для краткого ознакомления, но, если такая потребность возникнет, поможет вам освоить и более продвинутые темы.
Splines в 3ds Max и работа с ними
Для успешного 3D моделирования не всегда обязательно использовать только трехмерные объекты. Множество интересных и сложных объектов проще создавать с помощью сплайнов (Splines). Сплайны — это линии, которые обычно объединяются в плоские геометрические фигуры. Сплайны очень просты в управлении и позволяют легко создавать плоские объекты с множеством искривлений. Причем, плоские объекты легко можно превращать в трехмерные.
1. Примитивы
Для создания сплайнов нужно перейти в Create – Shapes – Splines и выбрать один из существующих примитивов. Примитивы – это готовые геометрические фигуры, состоящие из прямых или кривых. Создавать сплайны рекомендуется из ортогональных проекций (Top, Front, Right и т.д.)
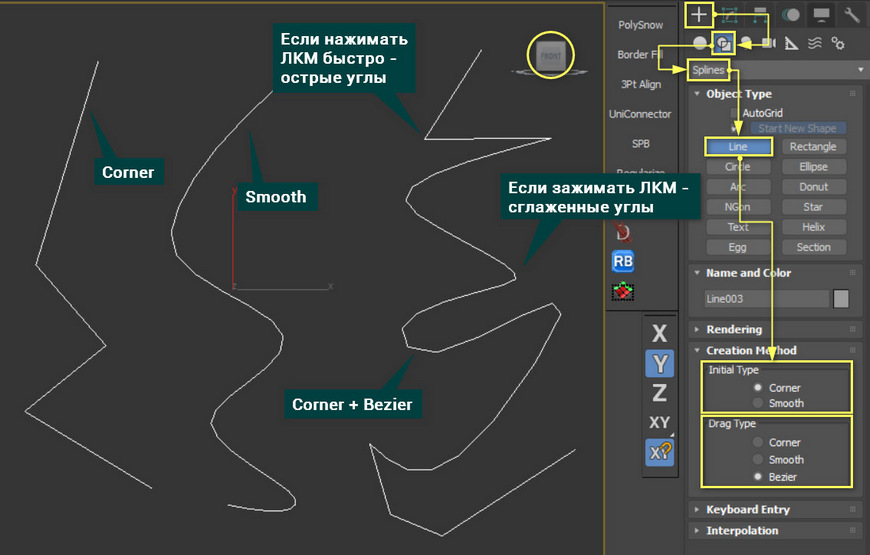
Line – основной примитив, который не имеет четкой формы. Он позволяет вручную создать фигуру любой формы. Причем фигура может быть как замкнутой, так и открытой. Line бывает трех видов: Corner (угловатая), Smooth (сглаженная) и Bezier (Безье).
Линия создается с помощью нажатия ЛКМ в рабочей области. Если нажатие было быстрое, то линия построится в зависимости от настройки Initial Type. Если ЛКМ была зажата на какое-то время, то часть линии построится в соответствии с разделом Drag Type. Линия будет строиться до тех пор, пока не окажется замкнута или пока не будет нажата ПКМ.
Все остальные примитивы замкнуты и имеют четкие параметры для настройки формы.
Rectangle – прямоугольник.
Circle – окружность.
Ellipse – эллипс. Внешне напоминает окружность, но настраивается иначе.
Arc – дуга.
Donut – двойная окружность (пончик, труба).
NGon– многоугольник с изменяемым количеством углов.
Star – звезда с изменяемым количеством исходящих «лучей».
Text – текст, состоящий из контуров различных знаков.
Helix – спираль. Уникальна тем, что среди перечисленных примитивов только она создается одновременно в 3х осях.
Egg – фигура, похожая на Donut, но имеющая форму яйца.
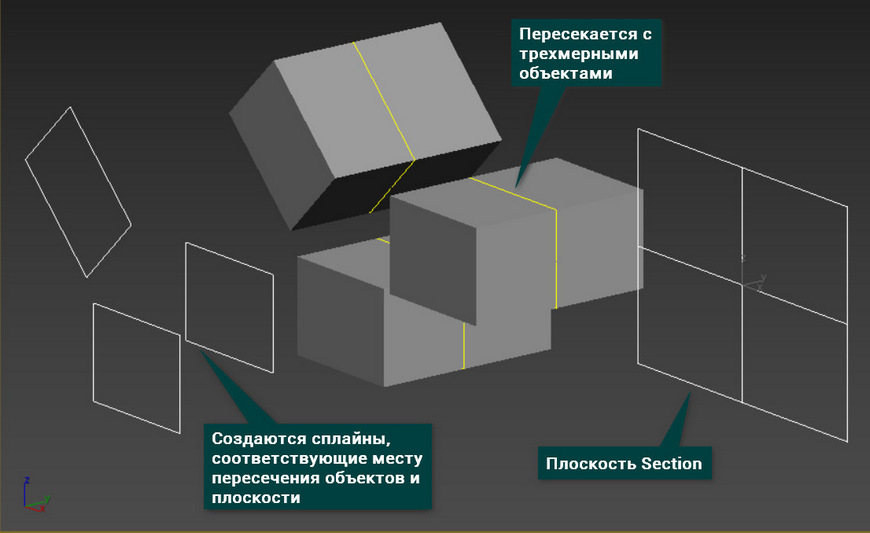
Section – плоскость, которая создает сплайны по форме других объектов. Новые сплайны создаются по форме объекта в зависимости от места пересечения с плоскостью.
2. Изменение объекта
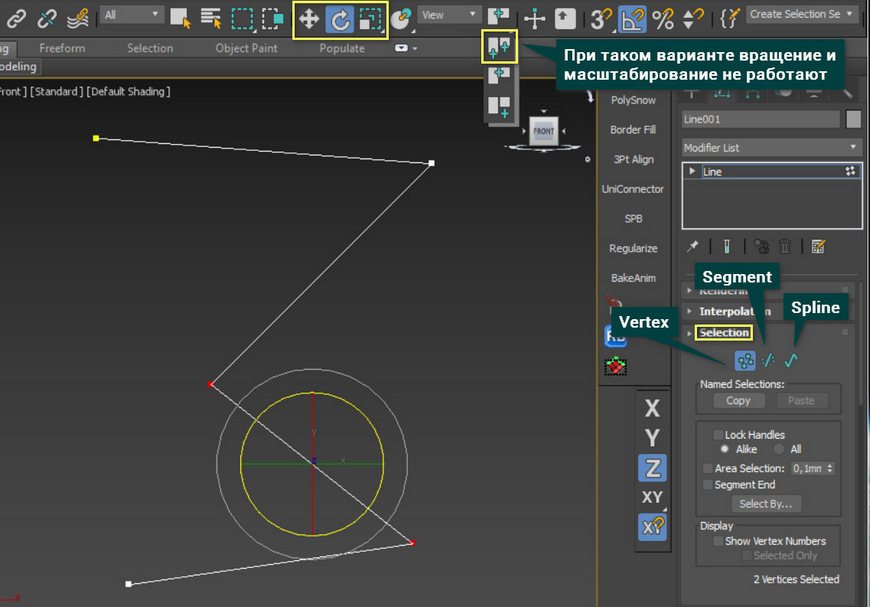
Все сплайны состоят из подобъектов: Vertex (точки) и Segment (сегменты). Для взаимодействия с этими подобъектами необходимо конвертировать примитивы в Editable Spline или использовать модификатор Edit Spline. Для Line это делать не обязательно.
Все точки и сегменты можно перемещать, вращать и масштабировать. Для этого нужно перейти в раздел Selection и выбрать тип подобъектов. Перемещать можно любые подобъекты и в любом количестве. Вращать точки можно только если выбрать две и более. К сегментам это не относится. У масштабирования такие же условия, как у вращения. Вращение и масштабирование могут не работать, если выбрана неверная настройка Use Selection Center. Все данные преобразования можно производить во всех осях.
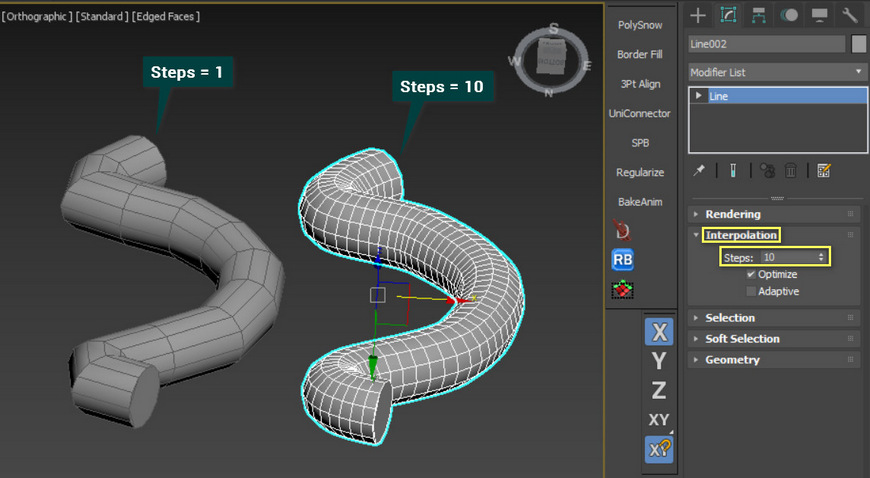
Interpolation – отвечает за плотность полигонов между точками. Это особенно важно для линий типа Smooth, чтобы при создании объема функцией Rendering, были более гладкими. Изменять плотность можно параметром Steps.
Geometry – раздел с большим набором функций, которой позволяет гибко редактировать один или несколько сплайнов. Значительная часть функций повторяет инструменты полигонального моделирования.
3. Превращение 2D в 3D
Все сплайны можно перевести в трехмерные объекты. Для этого можно воспользоваться модификаторами или задать размеры в разделе Rendering.
1) Модификаторы
Для использования модификаторов объект обязательно должен быть замкнутым. Если он будет открытым, то перестанет отображаться в рабочей области. Если объект состоит из двух непересекающихся закрытых сплайнов (Donut, Egg), то модификаторы будут действовать между линиями.
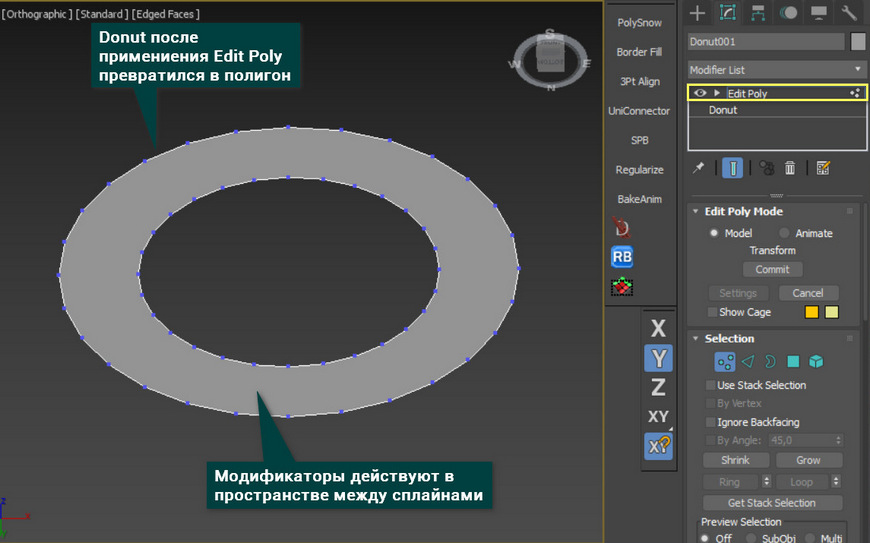
Edit Poly – превращает пространство внутри сплайнов в полигон. Не зависимо от формы объекта, количества углов и наличия внутренней формы, создастся один полигон. После этого объект можно редактировать методом обычного полигонального моделирования. Таким же образом работает и конвертация в Editable Poly.
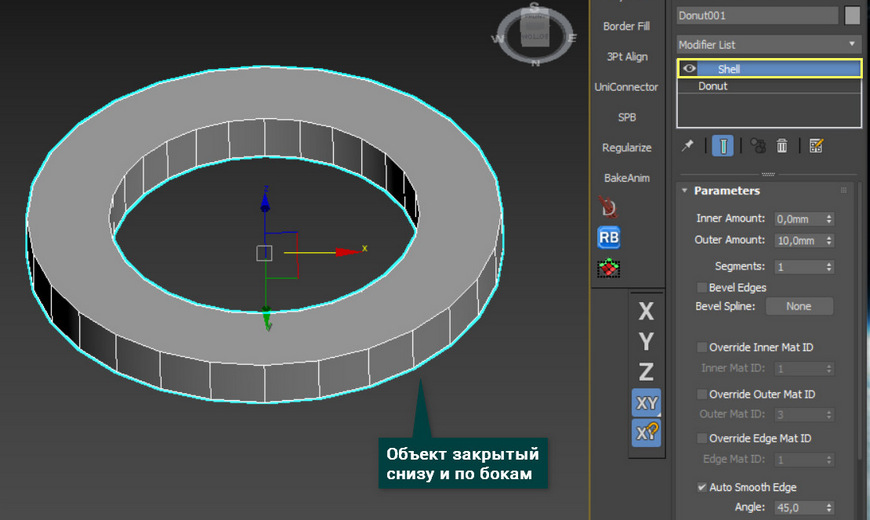
Shell – создает из двумерной фигуры объемны объект. В отличие от Edit Poly, сразу создаются боковые и нижние полигоны.
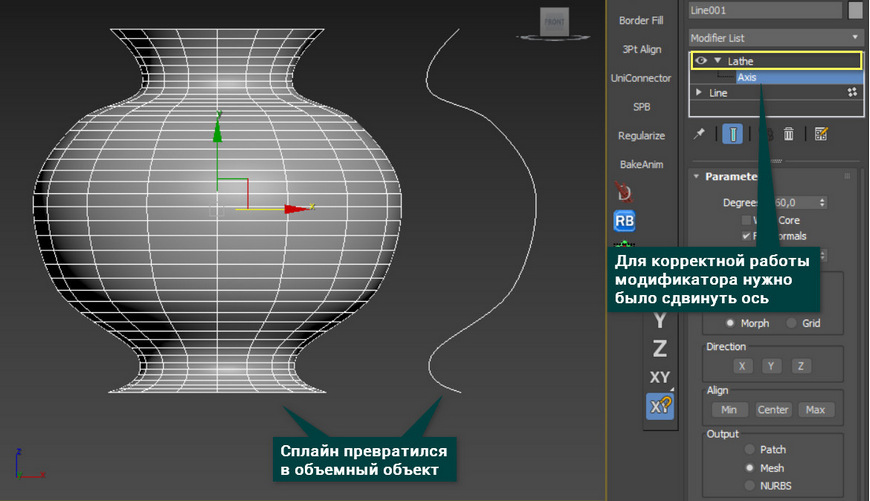
Lathe – превращает незамкнутый сплайн в круговой объект. Иногда для работы функции необходимо сдвинуть ось вращения. Для этого нужно открыть свиток модификатора, выделить Axis и переместить с помощью Select and Move.
После применения модификаторов сплайн превращается в полноценный полигональный объект. А про основы полигонального моделирования вы можете узнать в статье «Введение в полигональное моделирование 3ds Max».
2) Rendering
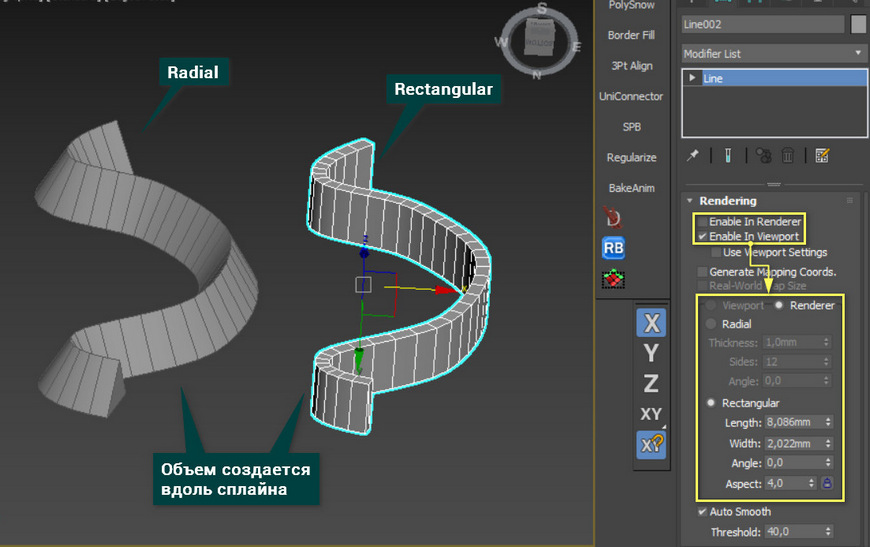
С помощью этого метода можно создать объем вдоль сплайна. Он может быть круговым (Radial) и прямоугольным (Rectangular). Для этого нужно включить флажки Enable In Renderer (объем виден при рендеринге) и Enable In Viewport (объем виден в рабочей области).
При выборе Radial можно изменять толщину (Thickness), количество граней (Size), угол поворота (Angle).
При выборе Rectangular можно изменять длину (Length), ширину (Width), угол поворота (Angle) и отношение длины к ширине (Aspect).
Сплайны применяются во многих инструментах моделирования. Чтобы получше познакомиться с этим типом объектов, рекомендую к прочтению:
Сплайны – великолепный инструмент для моделирования сильно искривленных объектов. Благодаря им можно моделировать провода, веревки, плинтусы. Некоторые инструмент используют сплайны как вспомогательные объекты для выполнения своих задач. Одним словом, сплайны используются в моделировании повсеместно. Поэтому каждый опытный пользователь 3ds Max просто обязан уметь ими пользоваться.
Что такое сплайны, для чего они нужны и как с ними работать
Вот основные формы сплайнов, которыми я обычно пользуюсь:
Все сплайны состоят из точек (vertex) и сегментов (segment):
Точки бывают четырех типов:
Чтобы изменить тип точки нужно выделить одну или несколько точек и нажать правую кнопку мыши. В контекстном меню выбрать нужный тип.
В разеделе Modify сплайны имеют несколько вкладок: Rendering, Interpolation, Selection, Soft Selection и Geometry.
Вкладка Rendering:
Вкладка Interpolation:
Вкладка Geometry:
Использование модификатора Shell, на примере создания объемного текста.
Создаем сплайн Text:
В поле Text меняем текст на нужный, изменяем размер (Size). Выбираем и стека модификаторов Shell. Затем задаем нужную степень выдавливания (Inner Amount или Outer Amount)
Модификатор Shell можно применять только к закрытым сплайнам (не имеющим разрывов). Вот пример использование модификатора Shell на сплайны Text, Line, NGon и Star:
Модификатор Sweep.
Сперва создаим любую линию. Я создал Line с прямыми углами (создается с нажатой клавишей Shift)
Далее из списка модификаторов выбираем Sweep и получаем следующий результат:
Модификатор Lathe.
Поздравляю! Вы дошли до самой интересной части урока.
Модификатор Lathe используется для создания объектов имеющих симметрию вращения (это могуть быть кувшины, бокалы, бутылки, колонны, стаканы и много другое).
Все что вам потребуется это нарисовать вертикальную линию в проекции Font и выбирать из списка модификаторов Lathe:
Нам сразу же нужно переместить ось симметрии, для этого нажимаем на плюсик справа от названия модификатора и выбираем Axis. Перемещаем Axis по оси Х :
Теперь проверьте включена ли у вас кнопка Show end result on/off toggle, которая находится под списком модификаторов. Включить её нужно для того, что бы видеть эффект всех модификаторов назначенных объекту:
Далее переходим к редактированию вершин (нажимаем на плюс слева от Line и выбираем Vertex), добиваемся желаемого результата. Можете добавлять\удалять точки, менять их тип и т.д.
Модификатор Lathe имеет несколько параметров, вот основные из них:
На этом третий урок окончен. В этот раз видеоурок состоит из двух частей: