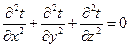для чего нужны условия однозначности
УСЛОВИЯ ОДНОЗНАЧНОСТИ ПРОЦЕССОВ ТЕПЛООБМЕНА
Для решения практических задач энергосбережения в строительстве и промышленности требуется знание теплового потока, градиента температур, распределения температур внутри объема тела. Поэтому для каждого конкретного случая к дифференциальному уравнению теплопроводности добавляют математические условия или ряд дополнительных уравнений, называемых условиями однозначности задачи.
Условия однозначности включают в себя геометрические, физические, временные и граничные условия.
Геометрические условия характеризуют геометрические и линейные размеры тела, участвующего в процессе теплообмена.
Физические условия характеризуют физические свойства тела, среды (X, с, р, а) или задается закон внутреннего тепловыделения.
Временные или начальные условия характеризуют особенности протекания процесса во времени или распределение температуры внутри тела в начальный момент времени: при т = 0 и Т = f (x, y, z). Очень часто в начальный момент времени тело имеет равномерную одинаковую температуру по всему объему: т = 0 и Т = Т0 = const.
Граничные условия характеризуют процессы теплообмена между поверхностью тела и окружающей средой.
Граничные условия задаются несколькими возможными случаями:
Q = а(Тп — Тс) или —X(dJ/dn) = а(Тп — Тс).
Вопросы стационарной и нестационарной теплопроводности для плоских, цилиндрических, тел сложной конфигурации, расчета температурных полей и энергосбережения рассмотрены в [13, 37].
Условия однозначности



Дифференциальное уравнение теплопроводности имеет бесчисленное множество решений. Для того, чтобы из этого множества выделить конкретное решение, дифференциальное уравнение нужно дополнить условиями однозначности.
Условия однозначности включают в себя:
— геометрические условия (форма и размеры тела);
— физические условия, характеризующие такие свойства тела, как теплопроводность, плотность, теплоёмкость;
— начальное условие, определяющее распределение температуры в теле в начальный момент времени;
— граничные условия, определяющие взаимодействие тела с окружающей средой.
Форма тела в значительной мере определяет выбор системы координат. Перенос тепла в параллелепипедах удобнее и проще описывать в прямоугольной декартовой системе координат. Для тел вращения больше подходит цилиндрическая система координат. Для сферических тел – сферическая система координат и т.д.
Начальное условие необходимо задавать при решении нестационарных задач. В общем виде это условие можно записать в виде:
при 
Граничные условия могут быть заданы различными способами. В зависимости от способа задания различают граничные условия первого, второго, третьего и четвёртого родов ( I, II, III, IV).
Граничные условия первого рода задают распределение температуры на поверхности тела

где 
Граничные условия второго рода задают значение плотности теплового потока для всех точек на поверхности тела.

Здесь n – нормаль к поверхности; x,y,z – координаты точек на поверхности тела. Такие случаи теплообмена обычно наблюдаются в нагревательных печах при радиационном теплообмене.

Коэффициент теплоотдачи зависит от большого количества факторов.
Граничные условия четвёртого рода задаются в области контакта двух твёрдых тел или твёрдого тела и жидкости. Такие граничные условия называются также сопряжёнными. Предполагается, что тепловой контакт является идеальным. В этом случае на поверхности контакта имеет место равенство температур двух тел, а также равенство плотностей теплового потока.


Граничные условия четвёртого рода физически являются наиболее точными, однако в случае контакта твёрдого тела с жидкостью их реализация сопряжена со значительными трудностями.
Условия однозначности для процессов теплопроводности
Так как дифференциальное уравнение теплопроводности выведено на основе самого общего закона термодинамики, то оно описывает явление теплопроводности в самом общем виде, т.е. оно описывает целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс теплопроводности и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями. Условия однозначности включают в себя:
1. Геометрические условия, которыми задаются форма и линейные размеры тела.
2. Физические условия, которыми задаются физические параметры тела (λ, с, ρ и др.) и может быть задан закон распределения внутренних источников теплоты.
3. Начальные условия, характеризующие распределение температуры в изучаемом теле в начальный момент времени. Начальные условия необходимы лишь при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальные условия аналитически могут быть записаны следующим образом (при τ = 0):
При равномерном распределении температуры в теле начальные условия упрощаются (при τ = 0):
4. Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой. Граничные условия могут быть заданы четырьмя способами.
I) Граничные условия I рода. Задается распределение температуры на поверхности тела для каждого момента времени:
В частном случае, когда температура на поверхности тела не изменяется во времени, и если она постоянна по поверхности, то
2) Граничные условия П рода.
В этом случае задаются значения плотности теплового потока для каждой точки поверхности тела и любого момента времени. Аналитически это можно представить следующим образом:
В простейшем случае, если плотность теплового потока по поверхности и во времени остается постоянной:
Такой случай теплообмена имеет место, например, при нагревании заготовок в высокотемпературных печах.
3) Граничные условия Ш рода.
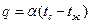

где α- коэффициент теплоотдачи, Вт/м 2 К, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой.
Коэффициент теплоотдачи α численно равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.
Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (по уравнению 20), должно равняться количеству теплоты, подведенному к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (по уравнению 9), т.е.
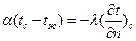
индекс «с» указывает на то, что температура и градиент относятся к поверхности тела (стенка).
Окончательно граничное условие Ш рода можно записать в виде
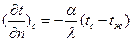
4) Граничные условия IV рода формируются на основании равенства тепловых потоков, проходящих через поверхность соприкосновения тела с окружающей средой или поверхность соприкосновения трердых тел, по закону теплопроводности, т.е.

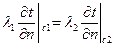
При совершенном тепловом контакте оба тела на поверхности соприкосновения имеют одинаковую температуру.
Таким образом, мы получили дифференциальное уравнение теплопроводности (16), которое совместно с условиями однозначности дает полную математическую формулировку конкретной задачи теплопроводности. Решение этой задачи может быть выполнено аналитическим, численным или экспериментальным методом. Ниже рассмотрим конкретные задачи процессов теплопроводности в различных телах аналитическим методом.
1.7. Стационарная теплопроводность плоских стенок (q 
Рассмотрим теплопроводность в плоских стенках при стационарном режиме (∂t/∂τ = 0) и отсутствии внутренних источников тепла (qv =0). В этом случае дифференциальное уравнение теплопроводности принимает вид:
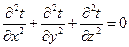
Условия однозначности для процессов теплопроводности



Так как дифференциальное уравнение теплопроводности выведено на основе самого общего закона термодинамики, то оно описывает явление теплопроводности в самом общем виде, т.е. оно описывает целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс теплопроводности и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями. Условия однозначности включают в себя:
1. Геометрические условия, которыми задаются форма и линейные размеры тела.
2. Физические условия, которыми задаются физические параметры тела (λ, с, ρ и др.) и может быть задан закон распределения внутренних источников теплоты.
3. Начальные условия, характеризующие распределение температуры в изучаемом теле в начальный момент времени. Начальные условия необходимы лишь при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальные условия аналитически могут быть записаны следующим образом (при τ = 0):
При равномерном распределении температуры в теле начальные условия упрощаются (при τ = 0):
4. Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой. Граничные условия могут быть заданы четырьмя способами.
I) Граничные условия I рода. Задается распределение температуры на поверхности тела для каждого момента времени:
В частном случае, когда температура на поверхности тела не изменяется во времени, и если она постоянна по поверхности, то
2) Граничные условия П рода.
В этом случае задаются значения плотности теплового потока для каждой точки поверхности тела и любого момента времени. Аналитически это можно представить следующим образом:
В простейшем случае, если плотность теплового потока по поверхности и во времени остается постоянной:
Такой случай теплообмена имеет место, например, при нагревании заготовок в высокотемпературных печах.
3) Граничные условия Ш рода.
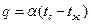
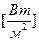
где α- коэффициент теплоотдачи, Вт/м 2 К, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой.
Коэффициент теплоотдачи α численно равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.
Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (по уравнению 20), должно равняться количеству теплоты, подведенному к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (по уравнению 9), т.е.
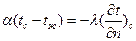
индекс «с» указывает на то, что температура и градиент относятся к поверхности тела (стенка).
Окончательно граничное условие Ш рода можно записать в виде
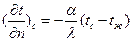
4) Граничные условия IV рода формируются на основании равенства тепловых потоков, проходящих через поверхность соприкосновения тела с окружающей средой или поверхность соприкосновения трердых тел, по закону теплопроводности, т.е.
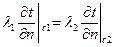
При совершенном тепловом контакте оба тела на поверхности соприкосновения имеют одинаковую температуру.
Таким образом, мы получили дифференциальное уравнение теплопроводности (16), которое совместно с условиями однозначности дает полную математическую формулировку конкретной задачи теплопроводности. Решение этой задачи может быть выполнено аналитическим, численным или экспериментальным методом. Ниже рассмотрим конкретные задачи процессов теплопроводности в различных телах аналитическим методом.
1.7. Стационарная теплопроводность плоских стенок (q
Рассмотрим теплопроводность в плоских стенках при стационарном режиме (∂t/∂τ = 0) и отсутствии внутренних источников тепла (qv =0). В этом случае дифференциальное уравнение теплопроводности принимает вид: