для чего нужны встроенные функции
Встроенные функции
Урок 26. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Встроенные функции»
· Что такое встроенные функции?
· Для чего нужны встроенные функции?
· Как работать со встроенными функциями?
Основные задачи электронных таблиц – это вычислять и анализировать данные, а также пересчитывать значения при изменении данных. Их основная цель – облегчение работы.
Все просто и понятно, если, например, нужно найти сумму трех чисел, записанных в ячейки электронной таблицы. А что делать, если нужно суммировать 1000 чисел? Вручную писать формулу? В таких случаях без встроенных функций не обойтись.
Встроенные функции – это функции, которые уже содержатся в табличном процессоре и выполняют различные вычисления автоматически при их вызове из библиотеки функций.
Каждая функция имеет свое собственное имя, которое необходимо для ее вызова. Имя функции – это не что иное, как сокращение от названия функции. Например, функция «сумма» в табличном процессоре называется СУММ.
На вкладке Формулы в разделе библиотека функций, в виде кнопки «автосумма» со значком выпадающего списка находятся функции, которые пользователи используют чаще всего, например, найти сумму, среднее арифметическое, максимальное и минимальное значение.
Давайте попробуем вызвать функцию при введении формулы. Например, нужно вычислить значение выражения 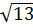
Рассмотрим несколько способов:
1 способ. Вызвать функцию можно просто набрав ее имя с помощью клавиатуры.
Итак, вводим «равно», теперь набираем на клавиатуре слово «КОРЕНЬ», теперь открываем скобку, в скобках можно ввести число с клавиатуры, можно указать ячейку или диапазон ячеек, теперь закроем скобку.
Данный способ неудобен тем, что при создании формул могут допускаться опечатки и синтаксические ошибки. Ссылки также лучше не вводить вручную, а указывать мышью ячейку или диапазон.
2 способ. Выбрать необходимую функцию из раскрывающегося списка.
Обратите внимание, вводим равно, теперь вводим букву «К», в раскрывшемся списке находим и выбираем необходимую нам функцию «Корень».
Мышкой указываем ячейку с числом, корень которого нужно вычислить.
3 способ. С помощью диалогового окна «Мастер функций».
Избежать ошибок при вводе имени функции и адресов ячеек позволяет использование Мастера функций.
Вызвать Мастера функций можно:
· Выбираем вкладку «Формулы», в разделе «Библиотека функций» нажимаем «Вставить функцию».
· Нажать кнопку «Вставить функцию» в строке формул.
· На вкладке «Формулы», в разделе «Библиотека функций» нажимаем «Автосумма». В выпадающем списке выберем пункт «Другие функции».
Обратите внимание! В ячейке автоматически появляется знак «равно».
Работа с мастером функций включает два шага.
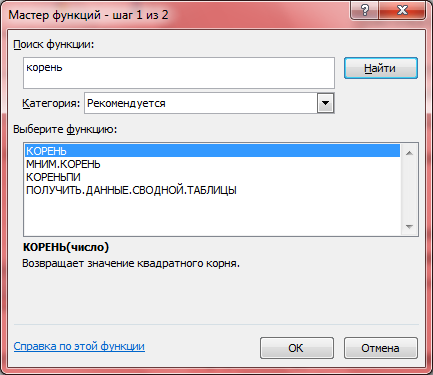
1 шаг: в окошке «Поиск функции» пишем название нужной нам функции, в нашем случае корень, и нажимаем кнопку «Найти». В окошке «Выберите функцию» выделяем необходимую функцию и нажимаем «ОК».
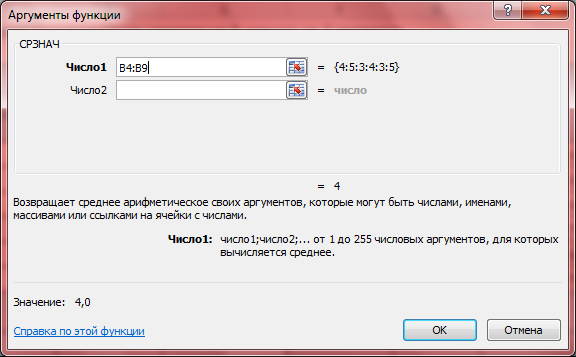
2 шаг: в появившемся окне «Аргументы функции» в окошко «число» вводим нужное нам число, либо выбираем ячейку или диапазон ячеек. Нажимаем ОК.
В табличном процессоре очень много стандартных функций. Поэтому их сгруппировали по категориям. Это математические, статистические, логические, текстовые, финансовые и другие. Список всех категорий можно посмотреть в окошке «Категория» Мастера функций.
Таким образом, использование функции делает формулу более компактной и понятной. В большинстве случаев использование функций в формулах позволяет не только упростить саму формулу, но и выполнять такие вычисления, которые осуществить по-другому, без функций, просто невозможно.
Решение задачи с использованием функций.
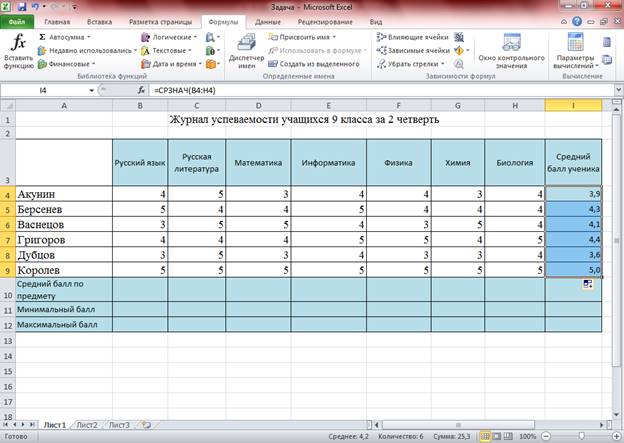
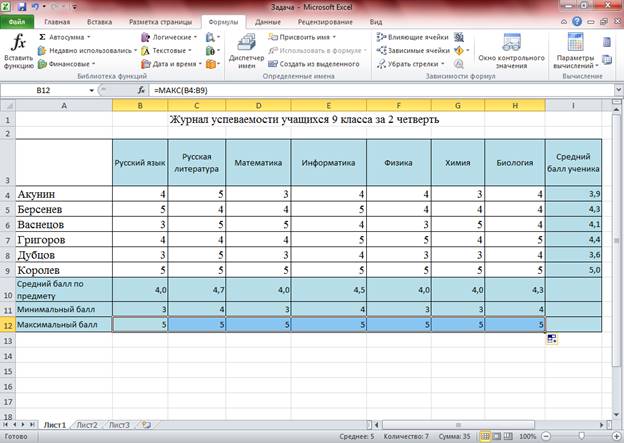
Нам дана таблица успеваемости учащихся 9 класса. Нужно вычислить средний балл каждого ученика, а также средний, минимальный и максимальный баллы по отдельным предметам.
Откроем файл «Успеваемость», находящийся в вашей рабочей папке.
В ячейку I4 введем формулу для вычисления среднего балла первого ученика. Для этого:
· В выпадающем списке кнопки «Автосумма» выберите функцию «среднее»;
· При необходимости отредактируйте диапазон ячеек, для которых вычисляется среднее значение.
Отредактировать диапазон ячеек можно тремя способами:
· исправить имя ссылки в строке формул;
· непосредственно в ячейке;
· Перетащить маркер заполнения в нужное вам место.
Нажмите клавишу «Enter».
Для вычисления средних баллов остальных учеников скопируем формулу из ячейки I4 в диапазон I5:I9. То есть, перетащим маркер заполнения в нужное нам место.
Теперь в ячейку В10 введем формулу для вычисления среднего балла по русскому языку. Сделаем это следующим образом:
· Выделим ячейку В10;
· На вкладке Формулы в разделе Библиотека функций нажимаем «Вставить функцию»;
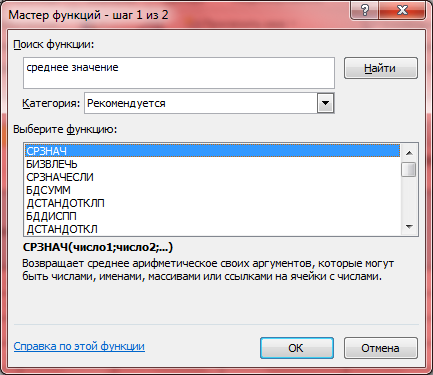
· В окошко «Поиск функции» напишем среднее значение и нажимаем кнопку «найти».
· В окошке «Выберите функцию» выделим СРЗНАЧ и нажимаем ОК.
· В появившемся окне диалога укажем диапазон ячеек, для которых вычисляем среднее арифметическое с помощью выделения этого диапазона мышью. Если диалоговое окно загораживает часть таблицы, его можно отодвинуть в сторону;
Скопируем формулу из ячейки В10 в диапазон С10:Н10.
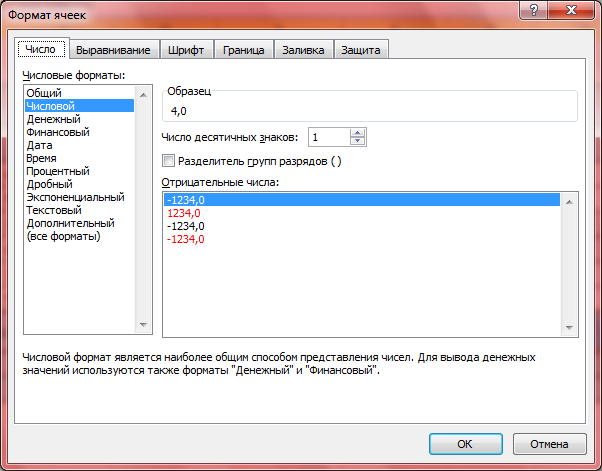
Установим для ячеек I4:I9 и В10:Н10 числовой формат с одним десятичным знаком. Для этого:
· Выделим нужные нам ячейки;
· Нажимаем на выделенной части правой кнопкой мыши;
· В раскрывшемся меню выберем «Формат ячеек»;
· Теперь в окошке числовые форматы выбираем «Числовой»;
· Слева, в окошке «Число» десятичных знаков выбираем один.
Аналогично вычислим минимальные и максимальные баллы по предметам.
Обратите внимание! Компьютер предлагает захватить лишние данные. Мы должны взять именно нужный диапазон ячеек, а не полагаться во всем на компьютер.
Сохраним таблицу в свою рабочую папку.
Заметьте, мы не пользовались калькулятором, не делали никаких вычислений в уме и только с помощью табличного процессора и встроенных функций сделали необходимые вычисления.
· Встроенные функции – это функции, которые уже содержатся в табличном процессоре и выполняют различные вычисления автоматически при их вызове из библиотеки функций.
· В табличном процессоре очень много стандартных функций. Поэтому их сгруппировали по категориям. Это математические, статистические, логические, текстовые, финансовые и другие.
· Список всех категорий можно посмотреть в окошке «Категория» Мастера функций.
· Использование функции делает формулу более компактной и понятной. В большинстве случаев использование функций в формулах позволяет не только упростить саму формулу, но и выполнять такие вычисления, которые осуществить по-другому, без функций, просто невозможно.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Встроенные функции и их использование.
§ 3. Встроенные функции и их использование
Информатика. 11 класса. Босова Л.Л. Оглавление
3.1. Общие сведения о функциях
В любом табличном процессоре используются встроенные функции.
Встроенная функция — это заранее написанная процедура преобразования данных.
Всё многообразие встроенных в табличные процессоры функций принято делить на категории по их назначению, выделяя среди них математические, статистические, логические, текстовые, финансовые и другие типы функций.
Каждая встроенная функция имеет имя — как правило, это сокращённое название производимого ею действия. Функции вызываются с некоторыми аргументами и возвращают единственное значение — результат обработки.
Аргументом функции может быть число, текст, выражение, ссылка на ячейку или диапазон ячеек, результат другой функции. Можно выделить функции:
• с одним аргументом, например КОРЕНЬ;
• с несколькими аргументами, количество которых фиксировано, например ОКРУГЛ;
• с нефиксированным количеством аргументов, например МАКС;
• с некоторыми необязательными аргументами, например РАНГ;
• без аргументов, например ТДАТА.
При использовании функции в формуле сначала указывается её имя, а затем в скобках указывается список аргументов через точку с запятой (табл. 1.4).
Таблица 1.4
Примеры записи функций в Microsoft Excel
Назначение каждой функции, наличие аргументов, их количество и тип можно посмотреть в Справке или в комментариях при вводе функции в формулу.
Вставить функцию в формулу можно несколькими способами:
1) использовать кнопки категорий функций в группе Библиотека функций вкладки Формулы на ленте;
2) воспользоваться инструментом Вставить функцию в группе Библиотека функций или в строке формул;
3) ввести функцию непосредственно в ячейку или в поле Строка формул.
Рассмотрим более подробно второй способ.
Если щёлкнуть на кнопке Вставить функцию строки формул, то откроется окно Мастер функций (рис. 1.5), а в текущую ячейку автоматически вставится знак «=» (если в этой ячейке ввод формулы ещё не начинался). В окне Мастер функций в списке поля Категория можно выбрать нужную категорию, после чего в списке поля Выберите функцию выбрать нужную функцию.
Рис. 1.5. Окно Мастер функций
После выбора имени функции в текущую ячейку автоматически вставляется имя функции и пара круглых скобок, а также открывается окно Аргументы функции с полями для ввода аргументов этой функции (рис. 1.6).
Рис. 1.6. Окно Аргументы функции функции СУММ
Если функция имеет фиксированное количество аргументов, то в окне Аргументы функции сразу отображается соответствующее количество полей для их ввода. Если функция имеет нефиксированное количество аргументов, то в окне сначала появляется несколько полей, а следующие поля появляются уже в процессе ввода аргументов.
Если аргументом является число или текст, то его нужно вводить в поле с клавиатуры. Если аргументом является ссылка на ячейки, то её также можно ввести с клавиатуры, но лучше выделить соответствующие ячейки с помощью мыши.
Для этого:
1) выберите кнопку Свернуть соответствующего поля для ввода аргумента функции (после этого окно Аргументы функции изменит свой вид: в нём кроме строки заголовка останется только это поле, а вместо кнопки Свернуть появится кнопка Развернуть;
2) выделите нужные ячейки (ссылки на них автоматически вставятся в соответствующее поле и в формулу);
3) выберите кнопку Развернуть (после этого окно Аргументы функции примет свой предыдущий вид);
4) при необходимости повторите шаги 1-3 для других аргументов функции;
5) после ввода в поля всех нужных аргументов функции выберите кнопку ОК.
Для некоторых функций Microsoft Excel автоматически предлагает первый аргумент. Например, для функции СУММ предлагается найти сумму чисел диапазона ячеек, заполненных числовыми данными, которые находятся над ячейкой с формулой (см. рис. 1.6) или слева от неё, если верхний диапазон ячеек пуст. Это предложение можно принять (если оно соответствует плану проводимых вычислений) или ввести вместо автоматически предложенного аргумента другой.
Два других способа вставки функции в формулу исследуйте самостоятельно. Назовите их основные отличия друг от друга. Что у них общего? Какой из способов будете применять вы?
В электронных таблицах используется большое количество встроенных функций. Познакомимся более подробно с теми из них, которые могут пригодиться вам в учебной и исследовательской деятельности, а также в повседневной жизни.
3.2. Математические и статистические функции
Для решения математических задач (решения уравнений, построения графиков функций) вам могут быть полезны функции, представленные в таблице 1.5. Здесь же представлены некоторые из статистических функций, позволяющих автоматизировать статистическую обработку данных. С их помощью можно вычислить наименьшее значение, подсчитать количество ячеек, содержащих заданную информацию, и т. д.
Таблица 1.5
Некоторые математические и статистические функции
Рассмотрим более детально работу статистической функции РАНГ, имеющую формат:
РАНГ(число; ссылка на список; [порядок])
Здесь:
• число — это число, для которого определяется ранг (порядок);
• ссылка на список — ссылка на список, которому принадлежит число (нечисловые значения в ссылке игнорируются);
• порядок — способ упорядочения значений списка:
0 или отсутствие параметра — определяет ранг (позицию, место) числа в списке так, как если бы список был отсортирован в порядке убывания (т. е. максимальному значению присваивается ранг равный 1, чуть меньшему числу — ранг 2 и т. д.);
число, не равное 0, — определяет ранг числа так, как если бы список сортировался в порядке возрастания (т. е. минимальному числу присваивается ранг 1, чуть большему числу — ранг 2 и т. д.).
Функция РАНГ присваивает повторяющимся числам одинаковый ранг. При этом наличие повторяющихся чисел влияет на ранг последующих чисел.
В ячейку В1 введена и скопирована в В2:В6 одна из двух следующих формул:
По какой из формул представлены результаты вычислений в столбце В?
Как вы можете объяснить отсутствие числа 2 среди значений ячеек диапазона С1:С6, если это — результаты вычислений по другой из приведённых выше формул?
3.3. Логические функции
Функция, результатом которой является ИСТИНА или ЛОЖЬ, называется логической.
К категории логических относятся функции ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ.
Функции И, ИЛИ, НЕ позволяют создавать составные логические выражения. Формат этих функций:
И(логическое_значение1; [логическое_значение2]; …)
ИЛИ(логическое_значение1; [логическое_значение2]; …)
НЕ(логическоезначение)
Аргументами функций И, ИЛИ, НЕ могут быть логические выражения или ссылки на ячейки, содержащие логические значения.
Функция ЕСЛИ имеет формат:
ЕСЛИ(лог выражение; значение_если_истина; значение_если_ложь)
Значение этой функции определяется так:
• если лог выражение имеет значение ИСТИНА, то значение функции равно значению выражения значение_если_ истина;
• если лог_выражение имеет значение ЛОЖЬ, то значение функции равно значению выражения значение_если_ложь. Табличные процессоры имеют и такие функции, которые вычисляют сумму, среднее арифметическое, количество не всех значений из диапазонов ячеек, а только тех, которые удовлетворяют определённому условию:
• функция СУММЕСЛИ вычисляет сумму тех чисел из указанного диапазона, которые удовлетворяют заданному условию;
• функция СРЗНАЧЕСЛИ вычисляет среднее арифметическое тех чисел из указанного диапазона, которые удовлетворяют заданному условию;
• функция СЧЁТЕСЛИ подсчитывает количество ячеек из указанного диапазона, содержимое которых удовлетворяет заданному условию.
Пример 1. Выясним, сколько решений имеет логическое уравнение
Преобразуем исходное уравнение, выразив импликацию через инверсию и дизъюнкцию:
Запишем формулу для вычисления логического выражения с помощью логических функций Microsoft Excel:
=ИЛИ(И(Х1;НЕ(Х2)); НЕ(ХЗ); Х4).
Внесём данные в таблицу и выполним расчёты — рис. 1.7.
Рис. 1.7. Решение логического уравнения (пример 1)
Итак, исходное уравнение имеет 13 решений — столько раз встречается значение ИСТИНА в диапазоне Е2:Е17. Для подсчёта этого значения можно воспользоваться функцией СЧЁТЕСЛИ.
Вспомните другой способ решения этого уравнения.
3.4. Финансовые функции
Финансовые функции используются для вычисления размеров выплат при погашении кредитов, банковских процентов на вклады, для определения процентной ставки и др.
1) Кредит — это ссуда, предоставленная кредитором (в данном случае банком) заёмщику под определённые проценты за пользование деньгами.
2) Вклад — денежные средства, внесённые физическим или юридическим лицом в финансовое учреждение на хранение, в рост или для участия в получении прибыли.
Аргументами этих функций являются:
• ставка — процентная ставка за период;
• плт — выплата, производимая в каждый период (месяц, квартал, год и т. п.);
• пс — приведённая (нынешняя) стоимость инвестиции;
• кпер — общее число периодов платежей по кредиту;
• бс — будущая стоимость инвестиции;
• тип — число 0, если оплата в конце периода; число 1, если оплата в начале периода (по умолчанию — 0).
Пример 2. Пусть ставка кредита в некотором банке составляет 18% годовых. Клиент хочет взять кредит на сумму 100 ООО руб. и может выплачивать банку по 4000 руб. ежемесячно. Нужно определить, за сколько периодов клиент сможет погасить этот кредит.
Функция КПЕР(ставка; плт; пс; [бс]; [тип]) возвращает количество периодов платежей для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки. Обязательные аргументы функции:
Получаем приблизительно 32 периода (месяца), т. е. более 2,5 лет.
Пример 3. Выясним, на какую сумму клиент может взять кредит, если ставка 19% годовых, а выплачивать он может по 12 000 руб. на протяжении двух лет (24 периода).
Функция ПС(ставка; кпер; плт; [бс]; [тип]) возвращает приведённую (к текущему моменту) стоимость инвестиции, представляющую собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
Обязательные аргументы функции:
• ставка (19%/12);
• кпер — общее количество периодов выплаты платежей по кредиту (24);
• плт (-12 000).
Формула для вычисления размера кредита будет иметь вид:
Получаем приблизительно 238 054 руб.
Пример 4. Пусть клиент хочет взять кредит 100 ООО руб. на 2 года. При этом выплачивать он может по 5000 руб. ежемесячно. Может ли он воспользоваться предложением банка, ставка по кредитам в котором составляет 20%?
Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) вычисляет процентную ставку за период (а не за год). Обязательные аргументы функции:
• кпер (24);
• плт (-5000);
• пс (100 000).
Формула для вычисления ставки будет иметь вид:
В результате вычислений получаем процентную ставку за месяц 1,51308%. Соответственно, процентная ставка за год составит 18,157% (1,51308 • 12).
Таким образом, клиенту не рекомендуется брать кредит в банке, ставка по кредитам в котором составляет 20%.
Пример 5. Клиент хочет сделать вклад на 3 года на сумму 300 000 руб. под 11% годовых с ежемесячным начислением процентов. Выясним, какую сумму он получит по окончании срока вклада.
Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки. Иначе говоря, с её помощью можно вычислить сумму, которую выплатят клиенту за вклад под определённые проценты по окончании срока вклада. Аргументы функции:
• ставка — годовая ставка в процентах, разделённая на количество периодов начисления процентов за год (в нашем примере это 11%/12);
• кпер — количество периодов начисления процентов (3 • 12 = 36);
• плт — сумма, которая добавляется к вкладу каждый период времени: 0 или отрицательное число (в нашем примере это 0, т. к. пополнение вклада клиентом не предусмотрено);
• пс — начальная сумма вклада (в нашем примере это 300 000).
Формула для вычисления суммы, которую клиент получит за вклад по окончании срока вклада, будет иметь вид:
В результате вычислений получаем 416 663,58 руб.
Пример 6. Клиент хочет сделать вклад на 2 года на сумму 100 000 руб. под 10,5% годовых с ежемесячным начислением процентов. При этом он имеет возможность ежемесячно пополнять вклад ещё на 2000 рублей. Выясним, какую сумму клиент получит по окончании срока вклада.
Формула для вычисления суммы, которую клиент получит за вклад по окончании срока вклада, будет иметь вид:
В результате вычислений получаем 176 409,84 руб.
Как изменится формула в примере 6, если клиент ежемесячно будет не пополнять счёт на 2000 руб., а снимать со счёта по 1000 руб.?
3.5. Текстовые функции
В основном табличные процессоры используются для работы с числами, но в них предусмотрена и возможность работы с текстом. Например, в электронные таблицы заносятся наименования товаров и услуг, фамилии, имена и отчества сотрудников, партнёров и клиентов, их адреса, телефоны и многое другое.
Для обработки текста в табличных процессорах имеется набор функций, которые можно использовать для определения длины текста, номера позиции первого вхождения символа в текст, части текста, который удовлетворяет определённому условию и др.
Аргументами текстовых функций могут быть текстовые данные (их нужно заключать в кавычки), ссылки на ячейки с текстом, ссылки на ячейки с числами.
Рассмотрим примеры некоторых текстовых функций Microsoft Excel.
Функция СТРОЧН преобразует все буквы обрабатываемого текста в строчные, а функция ПРОПИСН, наоборот, — в прописные. Функция ПРОПНАЧ делает прописной первую букву каждого слова, а все остальные буквы — строчными.
Функция СОВПАД позволяет сравнить две текстовые строки в Microsoft Excel. Если они в точности совпадают, то возвращается значение ИСТИНА, в противном случае — ЛОЖЬ (функция учитывает регистр, но игнорирует различие в форматировании).
Какое значение появится в ячейке С1, если в неё записать формулу =СОВПАД(А1; В1)? Какое значение появится в ячейке С2, если в неё скопировать формулу из ячейки С1?
Объясните следующий результат сравнения двух текстов:
Функция СЖПРОБЕЛЫ удаляет из текста все лишние пробелы, кроме одиночных между словами. Эту функцию полезно применять к данным, которые импортируются в рабочие листы Microsoft Excel из внешних источников.
Вспомните, как можно удалить все лишние пробелы из документа с помощью инструментов текстового процессора.
Кроме лишних пробелов импортируемые данные могут содержать и различные непечатаемые символы. Для удаления из текста всех непечатаемых символов предназначена функция ПЕЧСИМВ.
Выскажите свои предположения о назначении текстовых функций ДЛСТР, ЛЕВСИМВ, ПРАВСИМВ, ПСТР по результатам их работы:
Функция СЦЕПИТЬ последовательно объединяет значения указанных аргументов в одну строку.
Функция ПОВТОР повторяет текстовую строку указанное количество раз. Строка задаётся как первый аргумент функции, а количество повторов — как второй.
Чему равен результат вычисления по формуле ячейки С2, если результат вычисления по формуле ячейки А2 равен 6?
Функцию ПОВТОР можно применить и для «графического» представления числовых значений. Например, с её помощью можно визуализировать информацию об успеваемости некоторого ученика, получившего в текущем триместре 40 отметок «отлично», 45 — «хорошо» и 15 — «удовлетворительно».
Функции НАЙТИ и ПОИСК очень похожи. Они находят вхождение одной строки в другую и возвращают положение первого символа искомой фразы относительно начала текста. Различие в том, что первая учитывает регистр, а вторая — нет.
Какие значения будут отображены в ячейках А2 и В2?
Функция ПОДСТАВИТЬ заменяет определённый текст или символ на новое значение. Её применяют, когда заранее известно, какой текст необходимо заменить, а не его местоположение.
Функция ЗАМЕНИТЬ заменяет символы в заранее известном месте строки на новые. Функцию применяют, когда известно, где располагается текст, при этом сам он не важен.
1. Что будет отображено в ячейках В1 и В2?
2. С помощью какой из двух последних рассмотренных функций можно удалить все пробелы из текстовой строки? Как это сделать?
3. В ячейке содержится текст «колокол» (без кавычек). Что будет результатом вычислений по формуле:
=ДЛСТР(А1 )-ДЛСТР(ПОДСТАВИТЬ(А1; «о»;» «))?
4. Сформулируйте алгоритм подсчёта количества вхождений определённого символа в заданную строку.
САМОЕ ГЛАВНОЕ
В любом табличном процессоре используются встроенные функции — заранее написанные процедуры преобразования данных.
Каждая встроенная функция имеет имя — как правило, это сокращённое название производимого ею действия. Функции вызываются с некоторыми аргументами и возвращают единственное значение — результат обработки.
Аргументом функции может быть число, текст, выражение, ссылка на ячейку или диапазон ячеек, результат другой функции.
Всё многообразие встроенных в табличные процессоры функций принято делить на категории по их назначению, выделяя среди них математические, статистические, логические, текстовые, финансовые и другие типы функций.
Для решения уравнений, построения графиков функций и т. д. могут быть полезны математические функции.
Для автоматизации статистической обработки данных предназначены статистические функции. С их помощью можно вычислить наибольшее, наименьшее или среднее значение, подсчитать количество ячеек, содержащих заданную информацию, и т. д.
Функция, результатом которой является ИСТИНА или ЛОЖЬ, называется логической.
Финансовые функции используются для вычисления размеров выплат при погашении кредитов, банковских процентов на вклады, для определения процентной ставки и др.
Для обработки текста в табличных процессорах имеется набор функций, которые можно использовать для определения длины текста, номера позиции первого вхождения символа в текст, части текста, который удовлетворяет определённому условию и др.
Вопросы и задания
1. Раскройте суть математического понятия «функция». Что такое аргумент функции? Какие функции вы знаете из курса алгебры?
2. Что представляют собой функции в электронных таблицах? На какие категории они подразделяются?
3. Выясните, чему равен результат функции ОКРУГЛ, если заданное число разрядов больше нуля, меньше нуля, равно нулю.
4. Сколько аргументов могут иметь функции в электронных таблицах? Приведите примеры.
5. Данные каких типов могут быть аргументами функций? Приведите примеры.
6. Какие функции относятся к категории логических?
Оглавление
§ 3. Встроенные функции и их использование