для чего округлять числа
Округление чисел
Числа округляют, когда полная точность не нужна или невозможна.
Округлить число до определенной цифры (знака), значит заменить его близким по значению числом с нулями на конце.
Натуральные числа округляют до десятков, сотен, тысяч и т.д. Названия цифр в разрядах натурального числа можно вспомнить в теме натуральные числа.
В зависимости от того, до какого разряда надо округлить число, мы заменяем нулями цифру в разрядах единиц, десятков и т.д.
Если число округляется до десятков, то нулями заменяем цифру в разряде единицы.
Если число округляется до сотен, то цифра ноль должна стоять и в разряде единиц, и в разряде десятков.
Число, полученное при округлении, называют приближённым значением данного числа.
Записывают результат округления после специального знака « ≈ ». Этот знак читается как «приближённо равно».
При округлении натурального числа до какого-либо разряда надо воспользоваться правилами округления.
Поясним на примере. Округлим 57 861 до тысяч. Выполним первые два пункта из правил округления.
Теперь округлим 756 485 до сотен.
Округлим 364 до десятков.
Число 360 — приближённое значение с недостатком, а число 370 — приближённое значение с избытком.
В нашем случае, округлив 364 до десятков, мы получили, 360 — приближённое значение с недостатком.
Округлённые результаты часто записывают без нулей, добавляя сокращения «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард).
Округление также применяется для прикидочной проверки ответа в вычислениях.
Пусть нам нужно посчитать:
До точного вычисления сделаем прикидку ответа, округлив множители до наивысшего разряда.
794 · 52 ≈ 800 · 50 ≈ 40 000
Аналогично можно выполнять прикидку округлением и при делении чисел.
Округление натуральных чисел.
Округление мы часто используем в повседневной жизни. Если расстояние от дома до школы будет 503 метра. Мы можем сказать, округлив значение, что расстояние от дома до школы 500 метров. То есть мы приблизили число 503 к более легко воспринимающемуся числу 500. Например, булка хлеба весит 498 грамм, то можно сказать округлив результат, что булка хлеба весит 500 грамм.
Округление – это приближение числа к более “легкому” числу для восприятия человека.
В итоге округления получается приближенное число. Округление обозначается символом ≈, такой символ читается “приближённо равно”.
Можно записать 503≈500 или 498≈500.
Читается такая запись, как “пятьсот три приближенно равно пятистам” или “четыреста девяносто восемь приближенно равно пятистам”.
Разберем еще пример:
4 4 71≈4000 4 5 71≈5000
4 3 71≈4000 4 6 71≈5000
4 2 71≈4000 4 7 71≈5000
4 1 71≈4000 4 8 71≈5000
4 0 71≈4000 4 9 71≈5000
В данном примере было произведено округление чисел до разряда тысяч. Если посмотреть закономерность округления, то увидим, что в одном случае числа округляются в меньшую сторону, а в другом – в большую. После округления все остальные числа после разряда тысяч заменили на нули.
Правила округления чисел:
1) Если округляемая цифра равна 0, 1, 2, 3, 4, то цифра разряда до которого идет округление не меняется, а остальные числа заменяются нулями.
2) Если округляемая цифра равна 5, 6, 7, 8, 9, то цифра разряда до которого идет округление становиться на 1 больше, а остальные числа заменяются нулями.
1) Выполните округление до разряда десятков числа 364.
Разряд десятков в данном примере это число 6. После шестерки стоит число 4. По правилу округления цифра 4 разряд десятков не меняет. Записываем вместо 4 нуль. Получаем:
2) Выполните округление до разряда сотен числа 4 781.
Разряд сотен в данном примере это число 7. После семерки стоит цифра 8, которая влияет на то измениться ли разряд сотен или нет. По правилу округления цифра 8 увеличивает разряд сотен на 1, а остальные цифры заменяем нулями. Получаем:
3) Выполните округление до разряда тысяч числа 215 936.
Разряд тысяч в данном примере это число 5. После пятерки стоит цифра 9, которая влияет на то измениться ли разряд тысяч или нет. По правилу округления цифра 9 увеличивает разряд тысяч на 1, а остальные цифры заменяются нулями. Получаем:
4) Выполните округление до разряда десятков тысяч числа 1 302 894.
Разряд тысяч в данном примере это число 0. После нуля стоит цифра 2, которая влияет на то измениться ли разряд десятков тысяч или нет. По правилу округления цифра 2 разряд десятков тысяч не меняет, заменяем на нуль этот разряд и все разряды младшие разряды. Получаем:
13 0 2 894≈13 0 0000
Если точное значение числа неважно, то значение числа округляют и можно выполнять вычислительные операции с приближенными значениями. Результат вычисления называют прикидкой результата действий.
Например: 598⋅23≈600⋅20≈12000 сравним с 598⋅23=13754
Прикидкой результата действий пользуются для того, чтобы быстро посчитать ответ.
Примеры на задания по теме округление:
Пример №1:
Определите до какого разряда сделано округление:
а) 3457987≈3500000 б)4573426≈4573000 в)16784≈17000
Вспомним какие бывают разряды на числе 3457987.
8 – разряд десятков,
5 – разряд десятков тысяч,
4 – разряд сотен тысяч,
3 – разряд миллионов.
Ответ: а) 3 4 57 987≈3 5 00 000 разряд сотен тысяч б) 4 57 3 426≈4 57 3 000 разряд тысяч в)1 6 7 841≈1 7 0 000 разряд десятков тысяч.
Пример №2:
Округлите число до разрядов 5 999 994: а) десятков б) сотен в) миллионов.
Ответ: а) 5 999 99 4 ≈5 999 990 б) 5 999 9 9 4≈6 000 000 (т.к. разряды сотен, тысяч, десятков тысяч, сотен тысяч цифра 9, каждый разряд увеличился на 1) 5 9 99 994≈6 000 000.
Округление чисел в математике
Что такое округление чисел в математике
Округление числа до целых — замена числа ближайшим к нему натуральным числом или нулем.
Числа округляют и до других разрядов.
Для записи формулы округления используют знак «приблизительно равно» — ≈.
Виды округления, первое и второе правило
Числа округляют до определенного разряда.
Все следующие за нужным разрядом цифры — младшие разряды — заменяют нулями. Если они стоят после запятой, то отбрасывают.
Первое правило математического округления:
Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то предыдущая цифра остается без изменений.
Например, нужно округлить число 234 до разряда десятков.
Второе правило математического округления:
Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9, то предыдущая цифра увеличивается на единицу.
Например, нужно округлить 9768 до сотых.
Правила округления десятичных дробей
В десятичной дроби разряды после запятой при замене нулями на конце дроби справа не пишутся.
Округлить дробь 27,3156 до разряда сотых.
Алгоритм выполнения задания:
Округление натуральных чисел
Натуральные числа — числа, которые используют для счета объектов и предметов.
Для округления нужно:
Примеры решения задач
Округлить 45567 до сотен.
Округлить 4598 до десятков.
Округлить дробь 5,836 до разряда десятых.
Правила округления чисел после запятой

Всего получено оценок: 98.
Всего получено оценок: 98.
Округление очень часто встречается в физике и химии, однако правила округления чисел после запятой это именно математика. Правильно округлять достаточно просто, нужно лишь один раз запомнить принцип. Рассмотрим тему подробнее.
Что такое округление?
Нередко случаются ситуации, когда итогом вычисления служит бесконечное число. Это дробь с неограниченным числом знаков после запятой. Такое чаще всего возникает в результате деления чисел. Среди бесконечных дробей выделяют:
Циклическая бесконечная дробь в математике считается определенным числом, так как каждое следующее число можно предсказать. При этом простые бесконечные дроби вычисленными не считается. Наиболее известным не вычисленным числом считается число пи, у которого на сегодняшний день вычислено 2,7 триллиона знаков после запятой.
Зачем нужно округлять числа?
В математике числа округляют для записи в ответ. Запомните, только в редких случаях число после округления можно использовать в вычислениях. Дело в том, что каждое округление в процессе расчета отдаляет результат от реальности.
Это допустимо, когда расчетов меньше 10. Но в школе вырабатывается навык округления, а в профессиональной деятельности грубые ошибки недопустимы.
Кроме того, существует ряд ситуаций в физике, химии, инженерии, когда требуется выполнить грубый расчет. Для него так же можно использовать округление. Округляют результаты, как правило, до сотых. Это значит, что в числе после округления в числе после запятой должно остаться 2 знака.
Правила округления чисел
Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:
Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.
Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.
Что мы узнали?
Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.
Округление десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
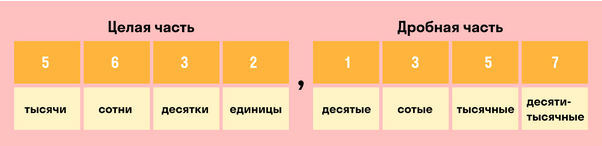
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
Еще одно правило округления, которое нужно запомнить
Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.
Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.
Примеры округления десятичной дроби
Давайте разберем несколько примеров округления дробной части десятичных дробей.
Пример 1. Округлите дробь 56,786 до сотых.
Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.
Справа от цифры округляемого разряда цифра 6.
Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.
Пример 2. Округлите дробь 0,647 до десятых.
Округляемая цифра — 6.
Смотрим пункт 3. Значит, цифра 6 остается неизменной.
Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.
Цифра, которую нужно округлить, — 3.
Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 4. Округлите дробь 3,286 до десятых.
Цифра, которую нужно округлить, — 2.
Согласно правилу, прибавляем: 2 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 5. Округлите дробь 45,387 до сотых.
Затем отбрасываем все остальные цифры, стоящие справа.