доказать что дерево двудольный граф

23.10.202326.06.2023 admin 0 Comments

Доказать, что всякое дерево является двудольным графом.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Правила и принципы форума «Высшая математика»	28.10.2009 15:17
	Открыта свободная публикация вакансий для математиков	26.09.2019 16:34
	Постдок позиция по математике в Гетеборге (Швеция)	10.09.2021 19:11

«Доказать, что всякое дерево является двудольным графом.»

Редактировалось 1 раз(а). Последний 31.01.2011 19:58.

Подвесим дерево за какую-нибудь вершину. Скажем, что это первый этаж. Все вершины, которые смежны с ней, образуют второй этаж. Все нерассмотренные вершины, которые смежны с вершинами второго этажа, поселим на третий этаж и т.д.

«Граф является двудольным тогда и только тогда, когда он не содержит цикла нечётной длины.»
Доказательство этого я нашёл.

«В дереве нет как четных, так и нечетных циклов.»
А есть како-либо доказательство этого? Или так и записывается в ответе к заданию?

Прошу прощения, если туплю, но я просто вообще ничего не смыслю в Теории графов.

Источник

Доказать, что всякое дерево является двудольным графом.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Запущен новый раздел «Задачки и головоломки»	29.08.2019 00:42
	Преподаватель мехмата МГУ удостоен международной премии по математике Presburger Award	28.07.2020 01:04
	Senior lecturer in Mathematics Linkoping (Швеция)	04.09.2021 23:16

«Доказать, что всякое дерево является двудольным графом.»

Редактировалось 1 раз(а). Последний 31.01.2011 19:58.

Прошу прощения, если туплю, но я просто вообще ничего не смыслю в Теории графов.

Источник

Русские Блоги

Решение по двудольному графу (DFS / BFS)

Каталог статей

1. Определение двудольного графа

Во-вторых, суждение о двудольном графе

Теорема 1. Необходимым и достаточным условием того, чтобы неориентированный граф G был двудольным графом, является:
1. G содержит не менее двух вершин.
2. Все длины циклов в G должны быть четными числами.
Другими словами, необходимое и достаточное условие для того, чтобы граф был двудольным, состоит в том, что граф не содержит циклов нечетной длины.

Итак, как этого добиться?
очень прост. Используется метод раскраски. Для неориентированного графа все вершины в графе сначала бесцветны. Мы начинаем с любой неокрашенной вершины и раскрашиваем эту вершину. Для и Для вершин, смежных с этой вершиной, есть три ситуации:
1. Undyed. Затем покрасьте эту вершину в цвет, отличный от цвета текущей вершины.
2. Он был раскрашен, но цвет текущей вершины другой, затем пропустите вершину.
3. Она окрашена, но такая же, как и текущая вершина. Тогда граф не является двудольным графом, и возврат не выполняется.
Если все вершины в графе раскрашены, и никакие смежные вершины не имеют одинаковый цвет, граф является двудольным.

Три, реализация кода

1. Идея реализации DFS описана в приведенном выше суждении о двудольном графе.

Проблема согласования и реализация двудольных графов подробно описаны в следующей статье:Алгоритм двудольного графа

Источник

Двудольные графы. Проверка графа на двудольность

Определение двудольного графа

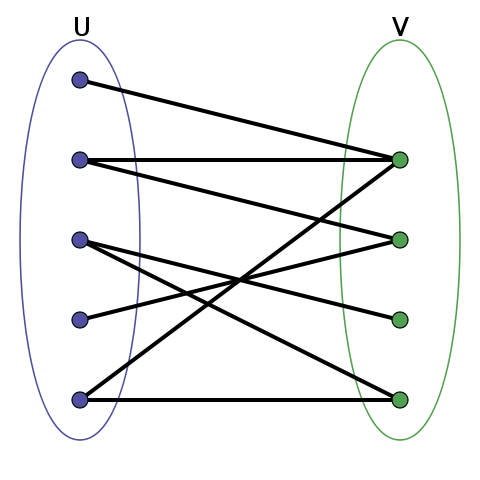
Часто в контексте двудольных графов используется понятие цвета вершины. Разбитие графа на две доли называется покраской его вершин в два различных цвета. Каждое ребро должно соединять вершины различного цвета.

Существует ещё один признак двудольности графа: граф является двудольным тогда и только тогда, когда в нём отсутствуют циклы нечётной длины.

Проверка графа на двудольность

Для проверки графа на двудольность и разбития его на доли чаще всего используется DFS.

Начинаем покраску с произвольной вершины, которую красим в произвольный цвет. При прохождении по каждому ребру красим следующую вершину в противоположный цвет. Если при переборе соседних вершин мы нашли вершину, уже покрашенную в тот же цвет, что и текущая, то в графе существует нечётный цикл, а значит, он не является двудольным.

Реализация

Хроматическое число графа

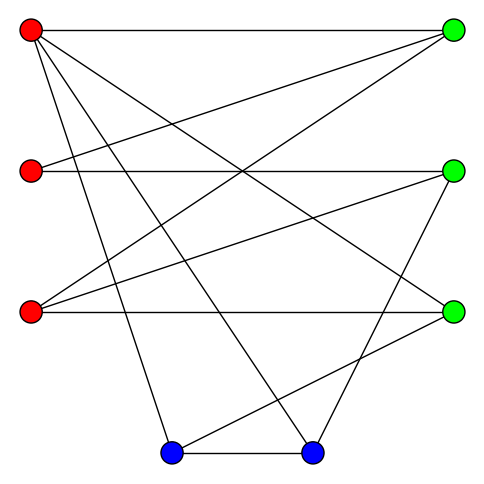
Определение двудольных графов обобщается на произвольное количество цветов. Хроматическим числом графа называется минимальное количество цветов, в которые можно покрасить его вершины так, чтобы каждое ребро соединяло вершины различного цвета. Хроматическое число двудольных графов равно \(2\), а хроматическое число графа, изображённого ниже, равно \(3\).

Задача проверки возможности покраски графа \(k\) цветами при \(k \ge 3\) не имеет эффективного (полиномиального) решения. Единственным доказанным решением является полный перебор всех покрасок за \(O(k^N)\). Эта задача является классической NP-полной (не имеющей полиномиального решения) задачей.

brestprog

Олимпиадное программирование в Бресте и Беларуси

Источник

Открытый урок по Дискретной математике «Двудольные графы. Полный двудольный граф. Изоморфные графы»

Федеральное агентство по образованию ФГОУ СПО

Тольяттинский политехнический колледж

по учебной работе

открытого урока по Дискретной математике

Тема: « Двудольные графы. Полный двудольный граф. Изоморфные графы »

Дата проведения: 08.11.06

Преподаватель: Малова Е.С.

Рассмотрено на заседании
цикловой комиссии
по специальности «Информатика и ВТ»
Председатель комиссии
________Л.Г. Светличная

План открытого урока

Тема урока: Двудольные графы. Полный двудольный граф. Изоморфные графы.

Дидактические: сформулировать основные понятия: двудольный граф, полный двудольный граф, изоморфные графы, научить учащихся правильно проверять пары графов на изоморфность.

Развивающие: развивать такие мыслительные операции, как анализ, синтез, обобщение, прививать умения выявлять общие свойства и находить различные элементы.

Воспитательные: воспитывать аккуратность, познавательную активность, внимание и организованность.

2. Основные знания и умения:

Знать : определение двудольного графа, полного двудольного графа, изоморфного графа.

Уметь: проверять граф на двудольность, проверять пару графов на изоморфность.

3. Вид урока : комбинированный урок.

4. К уроку приготовить : компьютер, плакат, рисунки в программе WORD

Проверка домашнего задания: решение задач (у доски)

Опрос по определениям, пройденным на уроках №33, №34

Полный двудольный граф

Методика проверки пары графов на изоморфность

2. Подведение итогов урока, оценки за урок

1. Пояснение к домашнему заданию

Проверка домашнего задания и опрос

Решение домашнего задания у доски

Свойства отображений (сюръекция, инъекция, биекция)

Понятие сюръекции (каждый элемент множества имеет свой прообраз)

Понятие инъекции (для каждого элемента существует не более одного прообраза)

Понятие взаимно однозначного отображения (сюръекция и биекция)

Понятие цикла в графе (Цепь называется циклом, если начальная и конечная вершины цепи равны)

Определение простого цикла (Цикл называется простым, если все его вершины различны).

Определение длины цикла (Число ребер цикла называют его длиной.)

Определение степени вершины (число ребер выходящих из нее)

Понятие смежных вершин (Две вершины называются смежными, если существует соединяющее их ребро)

Объяснение нового материала

Двудольный граф- это граф, у которого множество вершин V разбивается на два непересекающихся множества V ₁ и V ₂, причем всякое ребро из множества E соединяет вершину из V ₁ с вершиной из V ₂. Множества V ₁ и V ₂ называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющие множества V ₁ и V ₂, то он называется полным двудольным графом.

Теорема. Граф является двудольным, если все его простые циклы имеют четную длину.

Пример полного двудольного графа показываю на плакате. Комментарий: верхние три вершины на рисунке 1 содержатся во множестве V ₁, нижние принадлежат множеству V ₂.

Пример двудольного графа показывается на плакате. Комментарий: не все вершины на рисунке 2 из разных множеств соединены ребром, зато каждое ребро соединяет вершины из разных множеств.

Графы называются изоморфными, если существует взаимнооднозначное соответствие между их вершинами и ребрами и такое, что соответствующие ребра соединяют соответствующие вершины.

Существует два способа проверки графов на изоморфность:

1способ: В каждом графе определить

степень каждой вершины

смежность соответствующих вершин

Если результаты совпадают, то графы изоморфны, иначе не изоморфны

2 способ: преобразовать геометрически первый граф так, чтобы получился второй граф. Если это удалось сделать, то графы изоморфны, иначе не изоморфны.

Пример. Построить к звездочке изоморфные графы (показывается на компьютере, а студенты зарисовывают графы, полученные на рисунке 3)