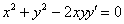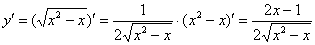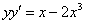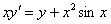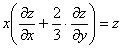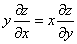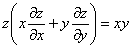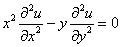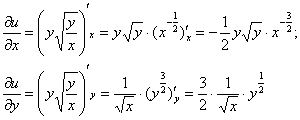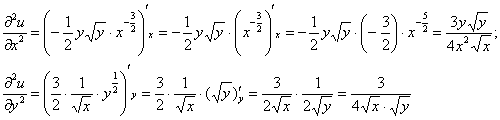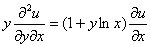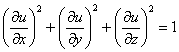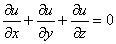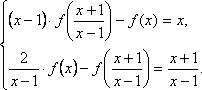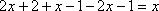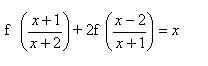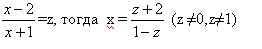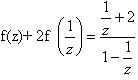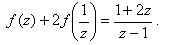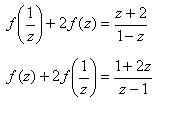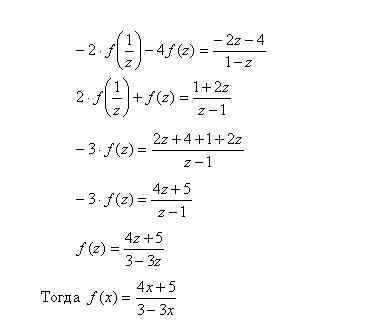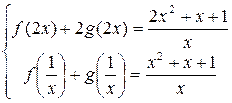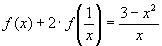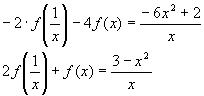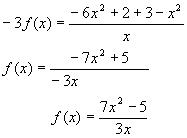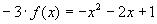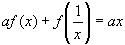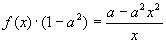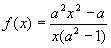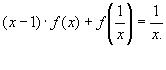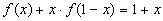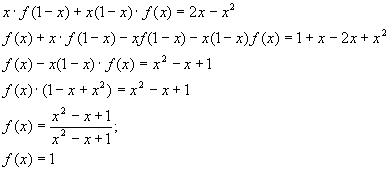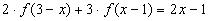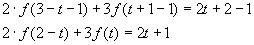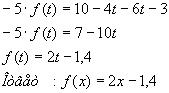доказать что функция удовлетворяет уравнению
Как проверить, удовлетворяет ли функция уравнению?
На дворе начало апреля 2015 и эти солнечные, но ещё холодные деньки навеяли ностальгические воспоминания о своих первых, во многом любительских заметках по высшей математике. Но время шло, тараканы взрослели, и мой стиль становился всё более и более академичным, а статьи – всё более объёмными и обстоятельными. Однако, не зря говорят, что всё возвращается на круги своя, и, видимо, поэтому сегодня появилось желание вернуться к той же лёгкости и непринуждённости изложения материала. По крайне мере, я попытаюсь =)
Задание, сформулированное в заголовке статьи, оказалось обойдено вниманием в теме «обычных» производных (производных функции 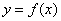
Проверить, удовлетворяет ли функция 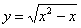
! Примечание: в условии таких задач производную нередко обозначают через 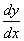
Решение: поскольку в предложенное уравнение входит не только функция, но и её производная, то сначала следует найти производную:
Далее решение можно оформить двумя эквивалентными способами:
Стиль №1. Подставим 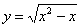
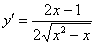
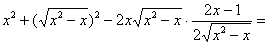
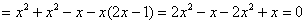
Что это, кстати, значит? Грубо говоря, функция 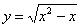
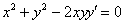
Стиль №2. Подставим 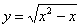
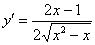
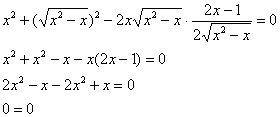
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Аналогичную проверку, разумеется, можно выполнить и для других функций. Так, например, подставим 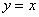
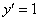
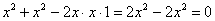
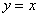
А вот, скажем, функция 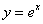
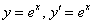
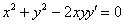
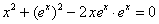
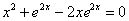
Совершенно понятно, что таких «неудовлетворительных» функций – великое множество.
Многие читатели уже давно интуитивно чувствуют нечто знакомое, и это неспроста! Всем с раннего детства знакома ситуация, когда, широко разинув рот, с интересом слушаешь взрослого, после чего там оказывается невкусная таблетка…, а то и вообще шприц в попе =) Вот и сейчас вы побывали в похожей ситуации! – неожиданно так, чтобы испугаться никто не успел, познакомил я вас с одной ужасной вещью:))
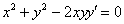
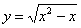
Проверить, удовлетворяет ли функция 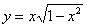
Здесь решение чуть выгоднее провести первым способом, т.е. найти производную и подставить 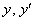
Проверить, удовлетворяет ли функция 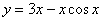
В этом же задании подстановка осуществляется в обе части уравнения и по этой причине удобнее использовать 2-й способ, получив верное либо неверное равенство.
Следует отметить, что функция вовсе не обязана удовлетворять уравнению, и иногда приходится давать противоположный ответ: «данная функция НЕ удовлетворяет данному уравнению». Но такой исход всегда неприятен, поскольку начинает мерещиться, что где-то допущена ошибка, после чего следует тщательная проверка, а зачастую и параноидальная перепроверка решения.
Примерные образцы чистового оформления примеров внизу страницы.
Как я уже намекнул в самом начале, рассматриваемое задание значительно чаще формулируется для функции нескольких, а точнее – для функции двух переменных; поэтому данный урок и оказался в разделе ФНП. Предполагается, что на данный момент вы умеете находить частные производные функции двух переменных:
Проверить, удовлетворяет ли функция 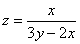
И сразу обращаю внимание на запись частных производных – в подавляющем большинстве подобных примеров вы встретите именно громоздкие обозначения. В принципе, уравнение можно переписать в виде 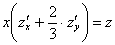
Решение: в предложенное уравнение входит как сама функция, так и её частные производные первого порядка, что сподвигает к естественным действиям: 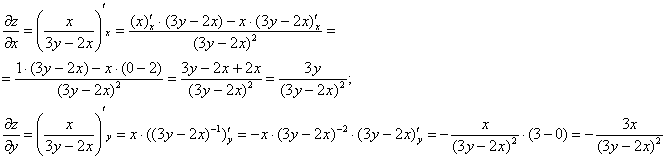
Решение, напоминаю, можно оформить двумя способами, и, на мой взгляд, здесь проще подставить найденные частные производные 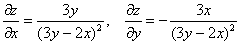
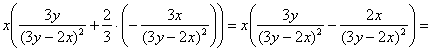
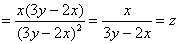
Ответ: данная функция удовлетворяет данному уравнению.
Пара примеров для самостоятельного решения:
Проверить, удовлетворяет ли функция 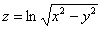
Тут сподручнее выполнить подстановку в обе части и получить верное или неверное равенство.
То же задание для функции 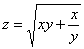
А здесь удобнее упростить левую часть и выяснить, получится ли в итоге 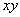
Предостерегаю от мысли «Да чего тут решать, и так всё понятно». Добросовестно прорешивая примеры, вы не только отрабатываете тематическую задачу, но и шлифуете свою технику нахождения частных производных. И это тем более важно, поскольку я предлагаю вам не абы какие-то задачки, а связный, методически продуманный курс статей – чтобы полученные знания и навыки остались с вами надолго. Таким образом, наш урок вовсе не закончился – он в самом разгаре!
Решения и ответы в подвале.
Помимо частных производных 1-го порядка, в уравнении могут присутствовать и частные производные более высоких порядков, как правило – второго:
Проверить, удовлетворяет ли функция 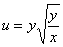
Здесь вместо буквы «зет» использована буква «у», что является весьма распространённым вариантом обозначения функции.
Решение: сначала найдём частные производные 1-го порядка:
Затем входящие в уравнение частные производные 2-го порядка:
Подставим 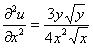
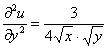
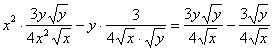
Ответ: данная функция не удовлетворяет данному уравнению.
Так действительно бывает!
Интересное задание для самостоятельного решения:
Проверить, удовлетворяет ли функция 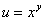
Краткое решение и ответ в конце урока.
И заключительные примеры посвящены тому же заданию, но с функцией 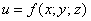
Проверить, удовлетворяет ли функция 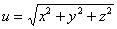
Решение: найдём частные производные 1-го порядка функции трёх переменных: 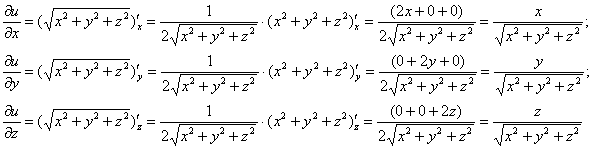
Симметрия это не только красиво – но ещё и очень удобно!
Теперь важно не перепутать квадраты производных с производными второго порядка. Подставим найденные производные в левую часть уравнения: 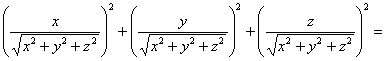
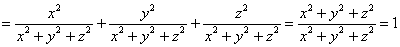
Ответ: дфуду
Вот так и рождаются новые ругательства =)
Симметрия по вашу душу:
Проверить, удовлетворяет ли функция 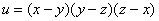
Подумайте, как рациональнее оформить решение.
Дополнительные задания по теме можно найти в задачнике Рябушко (ИДЗ 10.2), ну а я в лучших традициях своего «раннего творчества» отпускаю вас пораньше =) Сейчас ещё раз перечитаю текст и постараюсь избавить его от излишней наукообразной лексики…, хотя наставление в середине статьи всё-таки оставлю, что делать – старею =)
Надеюсь, мои уроки удовлетворяют вашим ожиданиям, и после перемены я жду вас на странице Частные производные неявно заданной функции.
Пример 2: Решение: найдём производную: 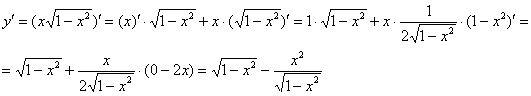
Подставим 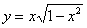
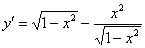
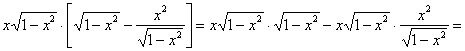
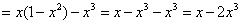
Ответ: данная функция удовлетворяет данному уравнению.
Пример 3: Решение: найдём производную: 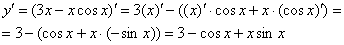
Подставим 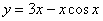
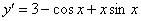
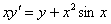
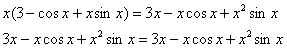
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 5: Решение: используя свойства логарифмов, преобразуем функцию: 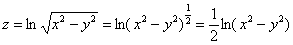
Найдём частные производные первого порядка: 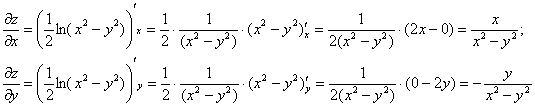
Подставим 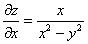
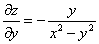
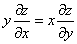
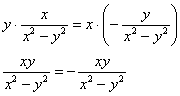
Получено неверное равенство.
Ответ: данная функция не удовлетворяет данному уравнению.
Пример 6: Решение: найдём частные производные первого порядка: 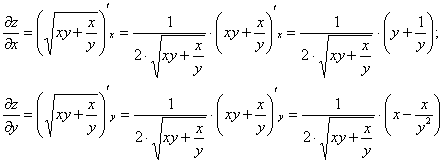
Подставим функцию и найденные производные в левую часть уравнения: 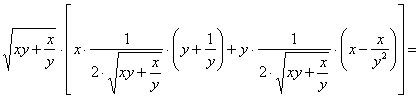
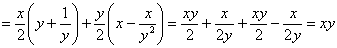
Ответ: данная функция удовлетворяет данному уравнению.
Пример 8: Решение: найдём частную производную по «икс»:
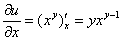
Найдём смешанную частную производную 2-го порядка:
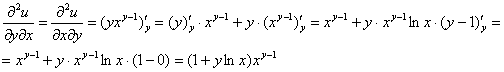
(т.к. константой считается «икс», то производная 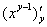
Подставим 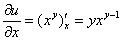
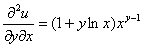
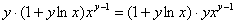
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 10: Решение: преобразуем функцию: 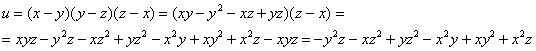
Найдем частные производные первого порядка: 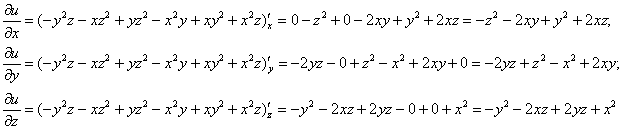
Подставим найденные производные в уравнение 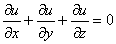
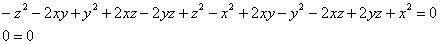
Получено верное равенство
Ответ: данная функция удовлетворяет данному уравнению.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Решение функциональных уравнений методом подстановки
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции, определённые на множестве 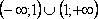
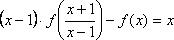
Решение:
Придадим x значение 

Отсюда 
Получим систему
Из уравнения (1) выразим 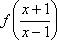
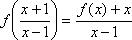
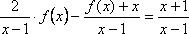
Отсюда 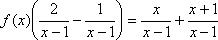


Проверим, действительно ли функция f(x) удовлетворяет уравнению 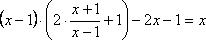
Ответ: 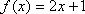
2. Найти функцию, удовлетворяющую уравнению
Решение:
2) Подставим в исходное уравнение, получим
3)Заменим z на 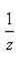
или после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
3.Пусть 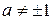

Решение:При замене
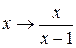

решением которой при a 2 ≠ 1 является функция
Ответ:
4.Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):
Решение:
В первом уравнении сделаем подстановку 2x = 1/z.
и первое уравнение принимает вид:
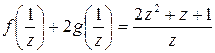
В результате получаем систему уравнений:
решение которой g(x) = 1/x, f(x) = x+1.
Ответ:g(x) = 1/x, f(x) = x+1.
Решение:
Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.
Решение:
Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.
f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)
Решение:
Решение:
9.Решите следующие функциональные уравнения.
Решение:
а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.
заменив теперь х- π/2 на х, имеем:
и с учетом предыдущего:
Положив х=0, получаем отсюда и из исходного уравнения:
Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.
10.
Решение: 1) Заменим 
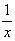
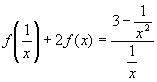

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
11. 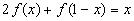
получим:
12.
Решение:
1) Заменим в уравнение 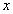
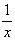
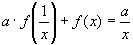
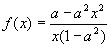
Решение:
1)Заменим в уравнении 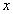
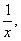
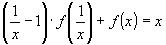
2)Выразим из исходного уравнения 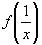
или 
3)Подставим 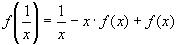
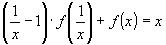

14.
Решение:
1.Заменим 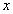
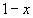
2.Умножим обе части уравнения 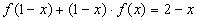

15.
Решение:1)Пусть 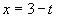
2)Пусть 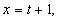
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
16.
Решение:
1) Заменим 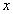
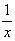
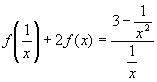

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением: