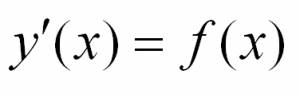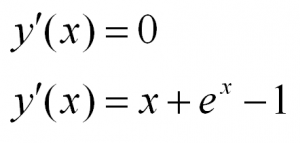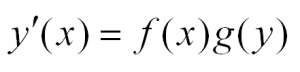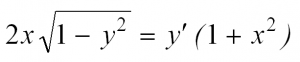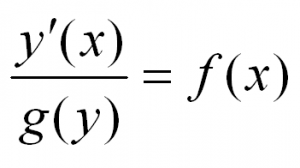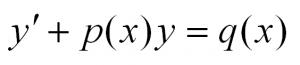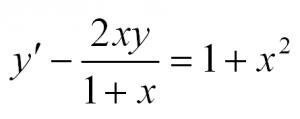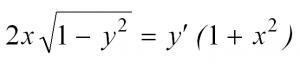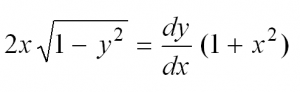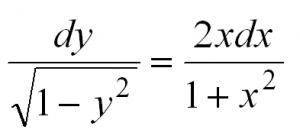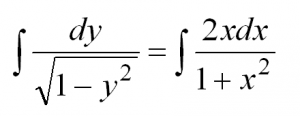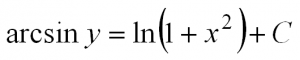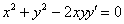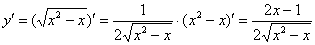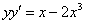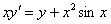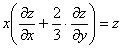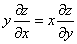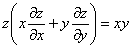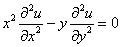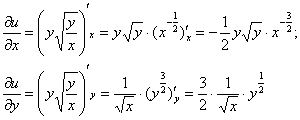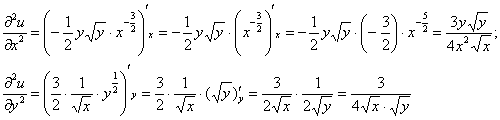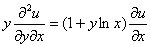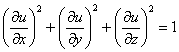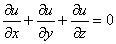доказать что функция является решением дифференциального уравнения
Дифференциальные уравнения для «чайников». Примеры решения
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
После этого останется проинтегрировать обе части и получить решение.
Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
Сначала перепишем производную в более привычном виде:
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:
Теперь осталось проинтегрировать обе части:
Интегрируем и получаем общее решение данного уравнения:
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Как проверить, удовлетворяет ли функция уравнению?
На дворе начало апреля 2015 и эти солнечные, но ещё холодные деньки навеяли ностальгические воспоминания о своих первых, во многом любительских заметках по высшей математике. Но время шло, тараканы взрослели, и мой стиль становился всё более и более академичным, а статьи – всё более объёмными и обстоятельными. Однако, не зря говорят, что всё возвращается на круги своя, и, видимо, поэтому сегодня появилось желание вернуться к той же лёгкости и непринуждённости изложения материала. По крайне мере, я попытаюсь =)
Задание, сформулированное в заголовке статьи, оказалось обойдено вниманием в теме «обычных» производных (производных функции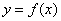 
), и, прежде чем перейти к примерам с функциями нескольких переменных, наверстаем упущенное:
Проверить, удовлетворяет ли функция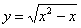 
уравнению 
! Примечание: в условии таких задач производную нередко обозначают через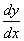 
, и это не должно сбивать с толку!
Решение: поскольку в предложенное уравнение входит не только функция, но и её производная, то сначала следует найти производную: 
Далее решение можно оформить двумя эквивалентными способами:
Стиль №1. Подставим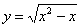 
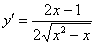
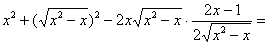
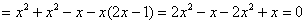
и 
в левую часть уравнения и проведём упрощения: 
– в результате получена правая часть, таким образом, данная функция удовлетворяет данному уравнению.
Что это, кстати, значит? Грубо говоря, функция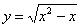 
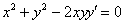
является корнем уравнения 
.
Стиль №2. Подставим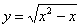 
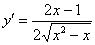
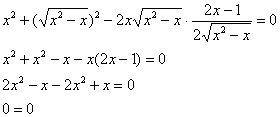
и 
в уравнение и выполним упрощения (в данном случае только левой части): 
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Аналогичную проверку, разумеется, можно выполнить и для других функций. Так, например, подставим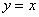 
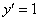
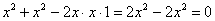
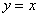
и её производную 
в левую часть уравнения (Стиль №1):
– получена правая часть, значит, функция 
тоже удовлетворяет данному уравнению.
А вот, скажем, функция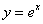 
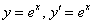
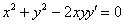
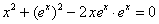
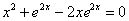
«не подходит». И действительно, подставляя 
в уравнение 
(Стиль №2): 
– получаем неверное равенство.
Совершенно понятно, что таких «неудовлетворительных» функций – великое множество.
Многие читатели уже давно интуитивно чувствуют нечто знакомое, и это неспроста! Всем с раннего детства знакома ситуация, когда, широко разинув рот, с интересом слушаешь взрослого, после чего там оказывается невкусная таблетка…, а то и вообще шприц в попе =) Вот и сейчас вы побывали в похожей ситуации! – неожиданно так, чтобы испугаться никто не успел, познакомил я вас с одной ужасной вещью:))
– это не что иное, как дифференциальное уравнение, а функция 
– одно из его решений. Дифференциальные уравнения мы научимся решать позже, а пока что проведём «артподготовку» к этой теме. Самостоятельно:
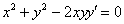
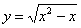
Проверить, удовлетворяет ли функция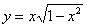 
уравнению 
Здесь решение чуть выгоднее провести первым способом, т.е. найти производную и подставить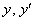 
в левую часть уравнения с дальнейшими преобразованиями.
Проверить, удовлетворяет ли функция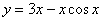 
уравнению 
В этом же задании подстановка осуществляется в обе части уравнения и по этой причине удобнее использовать 2-й способ, получив верное либо неверное равенство.
Следует отметить, что функция вовсе не обязана удовлетворять уравнению, и иногда приходится давать противоположный ответ: «данная функция НЕ удовлетворяет данному уравнению». Но такой исход всегда неприятен, поскольку начинает мерещиться, что где-то допущена ошибка, после чего следует тщательная проверка, а зачастую и параноидальная перепроверка решения.
Примерные образцы чистового оформления примеров внизу страницы.
Как я уже намекнул в самом начале, рассматриваемое задание значительно чаще формулируется для функции нескольких, а точнее – для функции двух переменных; поэтому данный урок и оказался в разделе ФНП. Предполагается, что на данный момент вы умеете находить частные производные функции двух переменных:
Проверить, удовлетворяет ли функция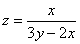 
уравнению 
И сразу обращаю внимание на запись частных производных – в подавляющем большинстве подобных примеров вы встретите именно громоздкие обозначения. В принципе, уравнение можно переписать в виде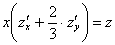 
и это ни в коем случае не будет ошибкой, но я буду придерживаться традиционного стиля, с которым вы вероятнее всего столкнётесь на практике.
Решение: в предложенное уравнение входит как сама функция, так и её частные производные первого порядка, что сподвигает к естественным действиям: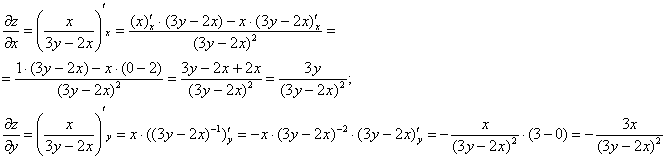 
Решение, напоминаю, можно оформить двумя способами, и, на мой взгляд, здесь проще подставить найденные частные производные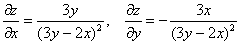 
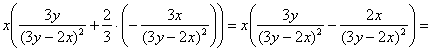
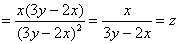
в левую часть: 
– «на выходе» получена правая часть нашего уравнения.
Ответ: данная функция удовлетворяет данному уравнению.
Пара примеров для самостоятельного решения:
Проверить, удовлетворяет ли функция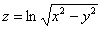 
уравнению 
Тут сподручнее выполнить подстановку в обе части и получить верное или неверное равенство.
То же задание для функции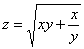 
и уравнения 
А здесь удобнее упростить левую часть и выяснить, получится ли в итоге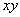 
.
Предостерегаю от мысли «Да чего тут решать, и так всё понятно». Добросовестно прорешивая примеры, вы не только отрабатываете тематическую задачу, но и шлифуете свою технику нахождения частных производных. И это тем более важно, поскольку я предлагаю вам не абы какие-то задачки, а связный, методически продуманный курс статей – чтобы полученные знания и навыки остались с вами надолго. Таким образом, наш урок вовсе не закончился – он в самом разгаре!
Решения и ответы в подвале.
Помимо частных производных 1-го порядка, в уравнении могут присутствовать и частные производные более высоких порядков, как правило – второго:
Проверить, удовлетворяет ли функция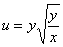 
уравнению 
Здесь вместо буквы «зет» использована буква «у», что является весьма распространённым вариантом обозначения функции.
Решение: сначала найдём частные производные 1-го порядка: 
Затем входящие в уравнение частные производные 2-го порядка: 
Подставим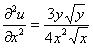 
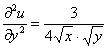
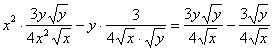
и 
в левую часть уравнения:
– в результате НЕ получена правая часть данного уравнения.
Ответ: данная функция не удовлетворяет данному уравнению.
Так действительно бывает!
Интересное задание для самостоятельного решения:
Проверить, удовлетворяет ли функция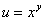 
уравнению 
Краткое решение и ответ в конце урока.
И заключительные примеры посвящены тому же заданию, но с функцией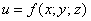 
трёх переменных. Следует отметить, что в «реальном» практическом примере вам вряд ли напишут, скольких переменных дана функция, и этот момент всегда следует прояснять самостоятельно:
Проверить, удовлетворяет ли функция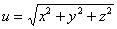 
уравнению 
Решение: найдём частные производные 1-го порядка функции трёх переменных: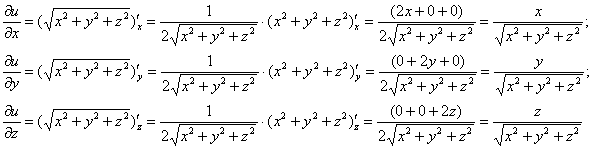 
Симметрия это не только красиво – но ещё и очень удобно!
Теперь важно не перепутать квадраты производных с производными второго порядка. Подставим найденные производные в левую часть уравнения: 
– получена правая часть данного уравнения.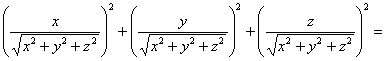
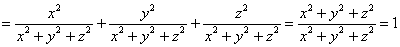
Ответ: дфуду
Вот так и рождаются новые ругательства =)
Симметрия по вашу душу:
Проверить, удовлетворяет ли функция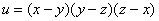 
уравнению 
Подумайте, как рациональнее оформить решение.
Дополнительные задания по теме можно найти в задачнике Рябушко (ИДЗ 10.2), ну а я в лучших традициях своего «раннего творчества» отпускаю вас пораньше =) Сейчас ещё раз перечитаю текст и постараюсь избавить его от излишней наукообразной лексики…, хотя наставление в середине статьи всё-таки оставлю, что делать – старею =)
Надеюсь, мои уроки удовлетворяют вашим ожиданиям, и после перемены я жду вас на странице Частные производные неявно заданной функции.
Пример 2: Решение: найдём производную: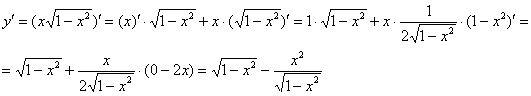 
Подставим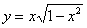 
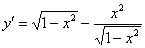
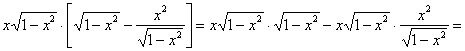
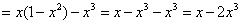
и 
в левую часть уравнения: 
– в результате получена правая часть данного уравнения.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 3: Решение: найдём производную: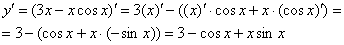 
Подставим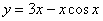 
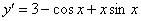
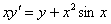
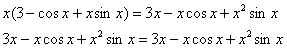
и 
в уравнение 
: 
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 5: Решение: используя свойства логарифмов, преобразуем функцию: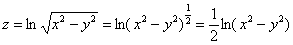 
Найдём частные производные первого порядка: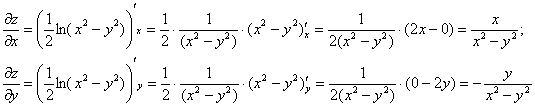 
Подставим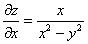 
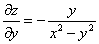
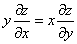
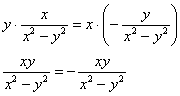
и 
в уравнение 
: 
Получено неверное равенство.
Ответ: данная функция не удовлетворяет данному уравнению.
Пример 6: Решение: найдём частные производные первого порядка: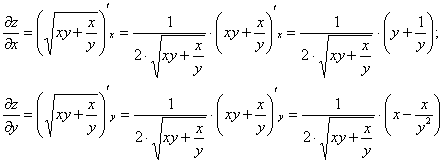 
Подставим функцию и найденные производные в левую часть уравнения: 
– получена правая часть данного уравнения.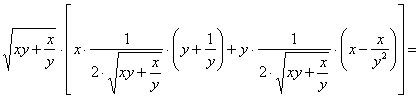
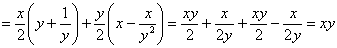
Ответ: данная функция удовлетворяет данному уравнению.
Пример 8: Решение: найдём частную производную по «икс»:
(т.к. константой считается «игрек», то производная берётся от степенной функции)
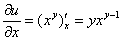
Найдём смешанную частную производную 2-го порядка:
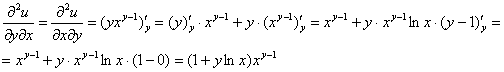
(т.к. константой считается «икс», то производная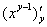 
берётся как производная от показательной функции)
Подставим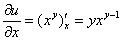 
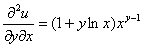
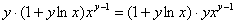
и 
в уравнение: 
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 10: Решение: преобразуем функцию: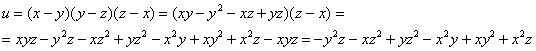 
Найдем частные производные первого порядка: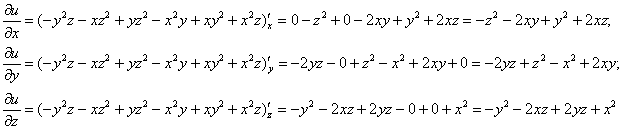 
Подставим найденные производные в уравнение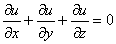 
:
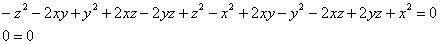
Получено верное равенство
Ответ: данная функция удовлетворяет данному уравнению.
Автор: Емелин Александр
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5