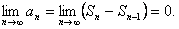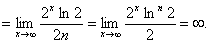доказать что гармонический ряд расходится
Необходимое условие сходимости ряда
Теорема: Если ряд сходится, то предел его общего члена равен нулю.
Доказательство: 
Расходимость гармонического ряда:
Гармонический ряд: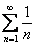 
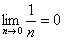
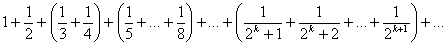
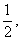
. Необходимое условие сходимости 
выполнено, однако 
Каждая из скобок превосходит 
потому частичные суммы неограниченно растут т.е. ряд расходится.
Стало быть, если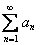 
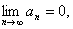
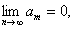
сходится, то 
но из того, что 
не следует сходимость ряда.
Следствие: Если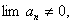 
то ряд расходится.
Примеры: 1)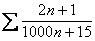 
расходится, т.к. 
2) 
расходится, т.к. 
(можно применить правило Лопиталя, получим) 
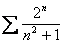
Ряд называют знакоположительным, если все его члены больше нуля, и знакоотрицательным, если все члены меньше нуля.
Знакоположительные и знакоотрицательные ряды называют знакопостоянными рядами. Если среди членов ряда конечное число членов имеет один знак, например, минус, а остальные члены другой знак, например, плюс, то отбросив частичную сумму, содержащую все слагаемые со знаком минус получим остаток ряда с положительными членами, т.к. остаток ряда определяет, сходится или расходится ряд, ряды с конечным числом членов одного знака можно рассматривать как знакопостоянные.
Знакопеременные ряды – ряды, содержащие бесконечное число как положительных, так и отрицательных слагаемых.
В знакопостоянных рядах последовательность частичных сумм монотонна, поэтому для сходимости ряда достаточна ограниченность последовательности частичных сумм.
Достаточные признаки сходимости для знакопостоянных рядов
Не ограничивая общности (см. свойство 1 для сходящихся рядов), будем формулировать признаки для знакопостоянных рядов.
Первый признак сравнения:
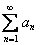
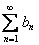
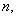
Пусть для членов рядов и 
выполнено условие: 
(вообще говоря, для всех 
начиная с какого-то номера, см. следствие из свойства 3 сходимости рядов), тогда:
а) если ряд с большими членами сходится, то и ряд с меньшими членами сходится;
б) если ряд с меньшими членами расходится, то и ряд с большими членами расходится.
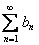
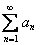
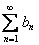
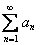
а) Если ряд сходится, то его частичные суммы возрастают и ограничены 
но частичные суммы ряда возрастают и не превосходят частичных сумм ряда , т.е. тоже ограничены, поэтому ряд сходится.
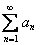
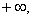
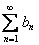
б) Если расходится, то его возрастающие частичные суммы должны стремиться в 
тогда и частичные суммы ряда неограниченно возрастают.
1) 
расходится т.к. 
, а — гармонический расходящийся ряд;
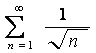
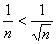
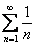
Чтобы распечатать файл, скачайте его (в формате Word).
Гармонический ряд
Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных числам натурального ряда:
Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних.
Содержание
Сумма первых n членов ряда
Отдельные члены ряда стремятся к нулю, нопредполагается чтосумма всех его членов расходится, т.е. что n-ное гармоническое число больше n-ного натурального. n-ной частичной суммой sn гармонического ряда называется n-ное гармоническое число, представляющее собой только сумму n первых членов гармонического ряда.:
Некоторые значения частичных сумм ( например для случая 1 слагаемого и 5-ти первых членов):
| S1 = 1; | S5 = 137/60 = приблизительно 2,283 |
Теоретико-числовые свойства частичных сумм: для любых n > 1 сумма первых n членов рядаSn будет дробным числом.
Формула Эйлера
В 1740 году Л. Эйлером было получено асимптотическое выражение для суммы первых n членов ряда. Теоретико-числовые свойства частичных сумм Для любых n>1
Сходимость ряда
Сходимость гармонического ряда можно продемонстрировать, сравнив его с числами натурального ряда: очевидно, что частичная сумма каждых n первых членов не может превышать такое же натуральное число n, которое равно числу членов гармонического ряда.
Рассмотрим известные доказательстване сходимости гармонического ряда
Доказательство Орема
Доказательство расходимости можно построить, группируя слагаемыетаким образом, чтобы сумма слагаемых в скобках была меньше 1/2. При этом получается ряд 1+1/2+1/2+. +1/2 +. :
Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).
Альтернативное доказательство расходимости
Предположим, что гармонический ряд сходится к сумме S:
В данном доказательстве также не учитывается тот факт, что каждому натуральному числу взаимооднозначно соответствует только один член гармонического ряда.
Частичные суммы
n-ая частичная сумма гармонического ряда, т.е. сумма только первых n членов ряда
Разница между различными гармоническими числами никогда не равна целому число и никакое гармоническое число, кроме 1, не является целым числом.
Связанные ряды
Ряд Дирихле
Обобщенным гармоническим рядом (или рядом Дирихле ) называют ряд, состоящий из членов гармонического ряда, возведенных в степень меньше или равную 1, или в степень большую 1. Считается, что Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1.
Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана от аргумента α.
Знакопеременный ряд
В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд
Его сумма равна натуральному логарифму 2:
Эта формула — частный случай Ряд Меркатора (англ.), ряда Тейлора для натурального логарифма.
Отметим, что если сходится гармонический ряд, то, естественно сходится и любой другой знакопеременный ряд, состоящий только из членов гармонического ряда.
Случайный гармонический ряд
«Истончённый» гармонический ряд
Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшаяся сумма сходится к числу Примечания
Расхождение гармонического ряда
Дорогой Юрий Степанович!)
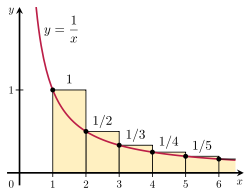
Почитайте про интегральный признак сходимости ряда.
Примените к данному ряду интегральный признак сходимости рядов, т.е. возьмите интеграл от 1/x, результатом будет функция ln(x), которая монотонно возрастает.
Это значит, что сумма частичного ряда с некоторым последним номером n пропорциональна натуральному логарифму от значения n.
А натуральный логарифм при стремлении x (то бишь n) в бесконечность также стремится в бесконечность)
Предлагаю Вам такое объяснение)))
А равенство, приведенное Вами и объяснения в Вашем источнике также вполне корректны, так как каждый член суммы слева больше (для первых трех) или равен (для четвертого) соответствующим членам суммы справа)
1\5+1\6+1\7+1\8>1\8+1\8+1\8+1\8 — Это верное неравенство)
Спасибо Вам огромное за интересный вопрос) Обращайтесь к нам еще!))
Гармонический ряд расходится потому, что:
1. Его частичная сумма примерно равна ln(n), а логарифм — функция неограниченная;
2. Любое рациональное число можно представить как египетскую дробь, то есть как сумму конечного числа членов гармонического ряда;
3. Можно выписать сколь угодно много наивных оценок, доказывающих расходимость гарм. ряда.
Вам мало различных доказательств? Тогда ищите — найдете еще.
«Его частичная сумма примерно равна ln(n)»
Да нет, примерно не равна:
где r = 0,5772. — постоянная Эйлера — Маскерони, а ln(n) — натуральный логарифм, е стремится к нулю при n, стремящемся к бесконечности.
Погрешность почти в 0.6 — это так, мелочь.
1. Предположим, что сумма гармонического ряда конечна и равна S.
2. Найдем такое n, что A=1+1/2+1/3+. +1/n>S.
3. S=A+1/(n+1)+1/(n+2)+. >A>S. Получили противоречие с предположением о сходимости ряда — значит он расходится.
Как найти «n» из пункта 2? Взять любую из оценок суммы подряд идущих членов — между степенями двойки, от n до 3n, и.т.д. Например
1/2+. +1/6>1;
1/7+. +1/21>1;
1/22+. +1/(22*3)>1
И.т.д. Складывая, получаем 1+. +1/6>2; 1+. +1/21>3; 1+. +1/66>4. Повторяя процедуру достаточное число раз, получим сумму, превосходящую S (для нормальных людей это самоочевидно, зануды могут воспользоваться аксиомой Архимеда).
Предлагаю на этом тему закрыть, по полочкам все уже разложено.
Если среднее гармоническое — это сложно, то единицы в оценках можно заменить на 2/3 без ущерба для дальнейшего, используя тривиальную оценку сумм: наименьшее слагаемое * количество слагаемых.
ДОКАЗАТЕЛЬСТВО сходимости гарм. ряда без интегралов.
По 2-му замечательному пределу
lim(1+1/n)^n=e.
Следовательно при любом n имеем (1+1/n)^n ln((n+1)/n),
1/n> ln(n+1)-lnn.
Отсюда 1>ln2
1/2>ln3-ln2
1/3>ln4-ln3
.
1/n>ln(n+1)-lnn
Cложив почленно эти неравенства, получим
Sn >ln(n+1)
Переходя к пределу при n, стремщемся к бесконечности, и принимая во внимание, что lim ln(n+1)=oo (бесконечности), получим, что и
limSn=oo (бесконечности)
т.е. гармонический ряд расходится.
1) » По 2-му замечательному пределу lim(1+1/n)^n=e.
Следовательно при любом n имеем (1+1/n)^n «
Из того, что последовательность чисел сходится к некоторому числу,
вовсе не следует, что каждый член последовательности меньше этого числа.
2) Автор темы написал, что логарифмов не знает.
Но их и не обязательно знать, чтобы понять расходимость гармонического ряда.
2) Что касается этого пункта, то мне кажется, стоит поощрить автора немного повысить свой уровень.Ведь логарифмы изучают в средн. школы. И без них нашему автору дальше шагу не ступить.
Интересно, а как у классиков? Классики тоже забывают
в нужном месте упомянуть и доказать возрастание последовательности?
У меня сейчас нет под рукой классиков, а было бы интересно это знать.
Как доказать что гармонический ряд расходится. Ряды для чайников
Как доказать что гармонический ряд расходится. Ряды для чайников
Введение
В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда :
1. Сумма первых n членов ряда
Отдельные члены ряда стремятся к нулю, но его сумма расходится. n-ной частичной суммой s n гармонического ряда называется n-ное гармоническое число:
1.1. Некоторые значения частичных сумм
1.2. Формула Эйлера
В 1740 году Л. Эйлером было получено асимптотическое выражение для суммы первых n членов ряда :
— формула Эйлера для суммы первых n членов гармонического ряда.
1.3. Теоретико-числовые свойства частичных сумм
2. Сходимость ряда
Гармонический ряд расходится очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10 43 элементов ряда).
Расходимость гармонического ряда можно продемонстрировать, сравнив его с телескопическим рядом:
частичная сумма которого, очевидно, равна:
2.1. Доказательство Орема
Доказательство расходимости можно построить, группируя слагаемые следующим образом:
Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).
2.2. Альтернативное доказательство расходимости
Предположим, что гармонический ряд сходится к сумме :
Тогда, перегруппируя дроби, получим:
Вынесем из второй скобки :
Заменим вторую скобку на :
Перенесём в левую часть:
Подставим обратно вместо сумму ряда:
Это равенство, очевидно, неверно, так как единица больше одной второй, одна треть больше одной четвёртой, и так далее. Таким образом, наше предположение о сходимости ряда ошибочно, и ряд расходится.
не равно 0, т.к. каждая из скобок положительная.
3. Частичные суммы
4. Связанные ряды
4.1. Ряд Дирихле
Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд
Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:
4.2. Знакопеременный ряд
Первые 14 частичных сумм знакочередующегося гармонического ряда (чёрные отрезки), показывающие сходимость к натуральному логарифму от 2 (красная линия).
В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд
Похожий ряд может быть получен из ряда Тейлора для арктангенса:
Это известно как ряд Лейбница.
4.3. Случайный гармонический ряд
Бирон Шмуланд из Университета Альберты рассмотрел свойства случайного ряда
4.4. «Истончённый» гармонический ряд
Сумма первых n членов ряда
Отдельные члены ряда стремятся к нулю, но его сумма расходится. n-ной частичной суммой s n гармонического ряда называется n-ное гармоническое число:
Некоторые значения частичных сумм
Формула Эйлера
Более точная асимптотическая формула для частичной суммы гармонического ряда:
Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена.
Теоретико-числовые свойства частичных сумм
Расходимость ряда
Гармонический ряд расходится очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10 43 элементов ряда).
Расходимость гармонического ряда можно продемонстрировать, сравнив его с телескопическим рядом :
частичная сумма которого, очевидно, равна:
Доказательство Орема
Доказательство расходимости можно построить, группируя слагаемые следующим образом:
Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).
Альтернативное доказательство расходимости
Связанные ряды
Ряд Дирихле
Обобщённым гармоническим рядом (или рядом Дирихле) называют ряд
Знакопеременный ряд
В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд
Похожий ряд может быть получен из ряда Тейлора для арктангенса :
Случайный гармонический ряд
В 2003 году изучены свойства случайного ряда
0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7 642 …,
«Истончённый» гармонический ряд
Напишите отзыв о статье «Гармонический ряд»
Примечания
Последовательности и ряды
(действия с числовыми рядами)
