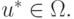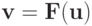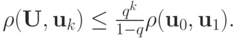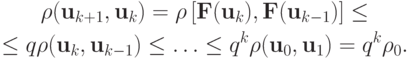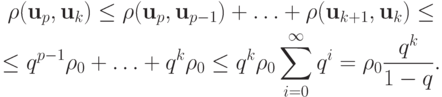доказать что отображение является сжимающим
Теория функций действительного переменного/Принцип сжимающиющихся отображений
> 
Всякое сжимающее отображение является непрерывным. Действительно, условие
\rho (x,y) 
Точка x называется неподвижной точкой отображения A, если имеет место равенство
Ax=x> 
Другими словами, неподвижная точка — это решение уравнения
Ax=x> 
x_<2>=Ax_<1>=A^<2>x_<0>>
x n = A x n − 1 = A n x 0 <\displaystyle
x_
x m = A m x 0 = A n ( A m − n x ) = A n x m − n <\displaystyle x_
По определению сжимающего отображения:
∑ k = 1 n − m α k − 1 = 1 − α n − m − 1 1 − α ≤ 1 1 − α <\displaystyle \sum _
Используем полученные соотношения:
A x = A ( lim n → ∞ x n ) = lim n → ∞ ( A x n ) = lim n → ∞ x n + 1 = x <\displaystyle Ax=A\left(\lim _
Существование неподвижной точки доказано.
Ax=x> 
Ay=y> 
По определению сжимающего отображения:
с другой стороны, по определению неподвижной точки:
\rho (Ax,Ay)=\rho (x,y)> 
Из этих двух соотношений можно вывести, что
x=y> 
Следует отметить, что доказательство принципа сжимающих отображений конструктивно: данная теорема не только доказывает существование единственного решения, но и указывает конкретный метод приближённого нахождения этого решения (называемый методом последовательных приближений или методом простой итерации).
Принцип сжимающих отображений может быть применён для доказательства существования и единственности решения различных видов уравнений. Ниже дан простейший пример применения принципа сжимающих отображений, ещё несколько примеров приведены в следующем разделе.
Пример [ править ]
Очевидно, что в этом случае f <\displaystyle
f> 
x_
сходится к решению уравнения
Рассмотрим теперь уравнение вида
F(x)=0> 
f(x)=x-\lambda F(x)>
и будем искать решение уравнения
x=f(x)> 
f ′ ( x ) = 1 − λ F ′ ( x ) <\displaystyle
f'(x)=1-\lambda F'(x)> 
то имеют место следующие неравенства
1 − λ K 2 ≤ f ′ ( x ) ≤ 1 − λ K 1 <\displaystyle 1-\lambda K_<2>\leq f'(x)\leq 1-\lambda K_<1>> 
Численное решение нелинейных алгебраических уравнений и систем
5.1. Сжимающие отображения. Итерации. Метод простых итераций (МПИ)
Рассмотрим системы нелинейных алгебраических уравнений, записанные в векторном виде.
Система нелинейных алгебраических уравнений
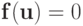 | ( 5.1) |
может быть также представлена в равносильном виде
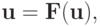 | ( 5.2) |
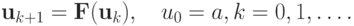 | ( 5.3) |
Приведем без доказательства одну из основных теорем функционального анализа.
Теорема (принцип сжимающих отображений). Всякое сжимающее отображение имеет в 
Более подробно о сжимающих отображениях и другие теоремы о неподвижных точках можно найти, например, в [5.1], [5.2], [5.3].
Теорема (о сжимающем отображении [5.1], [5.5].)
сходится к решению 
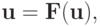
является сжимающим; при этом выполнено
По определению сжимающего отображения
В таком случае получим цепочку неравенств при p > k :
В соответствии с критерием Коши существования предела последовательности, последовательность < 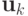
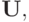
Принцип сжимающих отображений
Вопрос о существовании и единственности решений алгебраических, трансцендентных, дифференциальных и других типов уравнений можно сформулировать в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Одним из критериев существования и единственности неподвижной точки при такого рода отображениях является так называемый принцип сжимающих отображений.
Отображение 

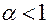




Точка 


Можно показать, что имеет место следующее утверждение.
Теорема (Принцип сжимающих отображений). Всякое сжимающее отображение, определенное в полном метрическом пространстве 
Принцип сжимающих отображений можно использовать для доказательства существования и единственности решений для уравнений различных типов. Следует отметить, что принцип сжимающих отображений позволяет не только доказать существование и единственность решения, но и дает метод нахождения приближенного решения. Этот метод называют методом итераций или методом последовательных приближений.
Рассмотрим применение этого метода к отысканию приближенного решения уравнения
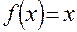
где функция 


с константой 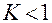

В этом случае 



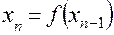
сходится к единственному корню уравнения (8.1).
Если функция 



где 
Пример 1. На промежутке 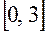

Записав данное уравнение в виде (8.1), получим

Легко проверяется, что производная 
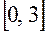
Пример 2. На промежутке 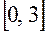

Как и в предыдущем примере запишем данное уравнение в виде

В этом примере производная 
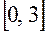

Геометрически метод итераций можно пояснить следующим образом. Построим на плоскости 





Отправляясь от некоторой точки 














Возможен также (рис.4) другой вид ломаной 


Если 
Пусть теперь требуется решить уравнение 



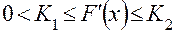
где 


где 
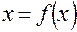

Так как 

Выберем теперь число 


Решая систему (8.5) двух уравнений относительно 


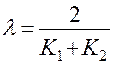
и заметим, что условие 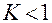
Пример. Требуется найти приближенное значение корня уравнения
на промежутке 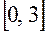
Легко проверяется, что 


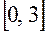

а тогда в соответствии с равенствами (8.6), получим


Введем в рассмотрение функцию
и используя метод итераций положим сначала 
То есть для получения искомого решения проделали 12 шагов.
Библиографический список
1. Вулих Б.З. Введение в функциональный анализ. ГИФМЛ, М, 1958.
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Изд-во «Наука». Гл. ред. физ-мат. лит. М. – 1972.
3. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений. Гос. Изд-во физ-мат. лит. М, 1962.
4. Треногин В.А. Функциональный анализ. Изд-во «Наука». Гл. ред. физ-мат. лит. М. – 1980.
5. Шилов Г.Е. Введение в теорию линейных пространств. Гос. Изд-во техн-теор. лит. М, 1956.
Предметный указатель
Глава 1. Линейные пространства. 5
§ 2. Определение линейного пространства. 7
§ 3. Свойства линейного пространства. 9
§ 4. Линейная зависимость. 12
§ 5. Базис и координаты.. 14
§ 7. Подпространства. 16
Глава 2. Евклидовы пространства. 19
§ 2. Определение евклидова пространства. 20
§ 3. Длина вектора. 22
§ 4. Неравенство Коши-Буняковского. 23
§ 5. Неравенство треугольника. 24
§ 6. Угол между векторами. 25
§ 7. Ортонормированный базис. 26
Глава 3. Линейные операторы.. 29
§ 1. Определение линейного оператора. 29
§ 2. Примеры линейных операторов. 33
§ 3. Действия над линейными операторами. 39
Глава 4. Преобразование координат. 43
§ 1. Замена базиса. 43
§ 2. Ортогональные преобразования. 46
§ 3. Матрица оператора при замене базиса. 48
Глава 5. Несовместные системы линейных уравнений и метод наименьших квадратов. 49
§ 1. Задача о проекции вектора и перпендикуляре к нему. 49
§ 2. Несовместные системы линейных уравнений. 50
§ 3. Метод наименьших квадратов. 54
Глава 6. Собственные векторы и собственные числа. 57
§ 1. Определение собственных векторов и собственных чисел. 57
§ 2. Вычисление собственных векторов и собственных чисел в конечномерном пространстве. 58
§ 3. Собственные векторы симметричных операторов. 62
Глава 7. Квадратичные формы и их приведение к каноническому виду. 64
§ 1. Приведение квадратичной формы к каноническому виду. 64
§ 2. Приведение двух квадратичных форм к каноническому виду. 73
§ 3. Малые колебания механических систем.. 78
Глава 8. Элементы теории метрических пространств. 82
§ 1. Определение метрического пространства. 82
§ 2. Сходимость. Полные метрические пространства. 84
§ 3. Принцип сжимающих отображений. 87
Библиографический список. 95
Предметный указатель. 96
Ольга Владимировна Афанасьева
Александр Алексеевич Потапенко
Функциональный анализ
В задачах управления
Редактор И.Н. Садчикова
Сводный темплан 2005 г.
Лицензия ЛР № 020308 от 14.02.97
№ 78.01.07.953.П.005641.11.03. от 24.11.2003 г.
Подписано в печать Формат 60´84 1/16
Б.кн.-журн. П.л. Б.л. РТП РИО СЗТУ
Северо-Западный государственный заочный технический университет
член Издательско-полиграфической ассоциации университетов России
191186, Санкт-Петербург, ул. Миллионная, 5
* Иногда апеллируя к привычным геометрическим представлениям, элементы линейного пространства называют не векторами, а точками; естественно, такое изменение названия не влечет никаких изменений в содержании изложенного.