доказать что плоскость пересекает отрезок ограниченный точками

Сборник задач по линейной алгебре и аналитической геометрии Учебное пособие (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

11.22.Доказать, что плоскость 3х-4у-2z+5=0 пересекает отрезок, ограниченный точками М1(3,-2,1) и М2(-2,5,2).

11.23. На оси Ох найти точку, равноудаленную от двух плоскостей:

11.24. На оси Оz найти точку, равноудаленную от точки М(1,-2,0) и от плоскости 3х-2у+6z-9=0.

11.25 Составить уравнения плоскостей, параллельных плоскости 2х-2у-z-3=0 и отстоящих от нее на расстоянии d=5.

11.26. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2х-14у+6z-1=0, 3х+5у-5z+3=0, в котором лежит начало координат.

11.27. Составить уравнение плоскости, которая делит пополам тупой двугранный угол, образованный двумя плоскостями: 3х-4у-z+5=0,

12. Уравнение прямой в пространстве.

12.1. Составить канонические уравнения прямой, проходящей через точку М(1,0,5) параллельно: 1) вектору , 2) прямой , 3) оси ОУ, 4) оси ОZ.

12.2. Составить канонические уравнения прямых, проходящих через точки: 1) А(1,3,4), В(2,5,-1); 2) А(3,1,0), В(-1,2,14); 3) А(8,-1,2), В(1,5,7); 4) А(1,8,4), В(3,3,3).

12.3. Составить параметрические уравнения прямой, проходящей через точку М(0,4,5) параллельно: 1) вектору , 2) прямой , 3) оси ОХ.

12.4. Составить параметрические уравнения прямой, проходящей через две данные точки: 1) А(7,3,2), В(1,4,10); 2) А(-1,-1,0), В(0,0,0); 3) А(4,0,11),

12.5. Через точки М1(-6,6,-5) и М2(12,-6,1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.

12.6. Даны вершины треугольника А(5,7,1), В(-3,3,9) и C(4,3,-7). Составить:

Параметрическое уравнение медианы, проведенной из вершины С. Каноническое уравнение биссектрисы внутреннего угла при вершине А. Параметрическое уравнение биссектрисы внешнего угла при вершине А. Каноническое уравнение высоты, опущенной из вершины В на сторону АС.

12.7. Параллельны ли следующие прямые?

12.8. Являются ли данные прямые перпендикулярными?

12.9. Вычислить угол между прямыми:

12.10. При каком следующие прямые

1) пересекаются, 2) параллельные, 3) скрещиваются, 4) совпадают.

12.11. Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями

12.12. Составить параметрические уравнения движения точки М(х, у,z), которая, имеет начальное положение М0(3,-1,-5), движется прямолинейно и равномерно в направлении вектора со скоростью V=21.

12.13. Составить уравнения движения точки М(х, у,z), которая двигаясь прямолинейно и равномерно, прошла расстояние от точки М1(-7,12,5) до точки М2(9,-4,-3) за промежуток времени от t1=0 до t2=4/

12.14. Точка М(х, у, z) движется прямолинейно и равномерно из начального положения М0(20,-18,-32) в направлении, противоположном вектору со скоростью V=26. Составить уравнение движения точки М и определить точку, с которой она совпадает в момент времени t=3.

12.15. Составить уравнения прямой, которая проходит через точку М1(-4,-5,3) и пересекает две прямые:

13. Взаимное расположение прямой и плоскости в пространстве.

13.1. Найти точку пересечения прямой и плоскости:

13.2. Составить уравнение плоскости, проходящей через точку М0(1,-1,-1) перпендикулярно прямой .

13.3. При каком значении m прямая параллельна плоскости .

13.4. При каком значении В прямая

параллельна плоскости .

13.5. При каких А и D прямая

лежит в плоскости .

13.6. При каких значениях А и С плоскость перпендикулярна к прямой .

13.7. При каких значениях m и В прямая

перпендикулярна к плоскости .

13.8. Найти точку Q симметричную точке Р(2,-5,7) относительно прямой, проходящей через точки М2(-2,-17,-8) и М1(5,4,6)

13.9. Найти проекцию точки Р(5,2,1) на плоскость .

13.10. На плоскости Оху найти такую точку Р, сумма расстояний от которой до точек А(-1,2,5) и В(11,-16,10) была бы наименьшей.

13.11. Точка М(х, уz) движется прямолинейно и равномерно из начального положения М0(15,-24,-16) со скоростью V=12 в направлении вектора . Убедившись, что траектория точки М пересекает плоскость найти:

1) точку их пересечения Р.

2) время, затраченное на движение точки М от М0 к Р.

3) длину отрезка М0Р.

13.12. Точка М(х, уz) движется прямолинейно и равномерно из начального положения М0(28,-30,-27) со скоростью V=12,5 по перпендикуляру, опущенному из точки М0 на плоскость . Составить уравнение движения точки М и определить:

1) точку Р пересечения ее траектории с этой плоскостью.

2) время, затраченное на движение точки М от М0 до Р.

3) длину отрезка М0Р.

13.13. Вычислить расстояние d от точки Р(2,3,-1) до следующих прямых:

13.14. Составить уравнение плоскости, проходящей через точку А(5,1,8) параллельно прямым

13.15.Составить уравнение плоскости, проходящей через прямую и точку (1,2,1).

13.16. Доказать, что прямые и лежат в одной плоскости и составить уравнения этой плоскости.

13.17 Найти проекцию точки С(3,-4,-2) на плоскость, проходящую через параллельные прямые и .

13.18. Найти точку Q, симметричную точке Р(3,-4,-6) относительно плоскости, проходящей через М1(-6,1,-5), М2(7,-2,-1) и М3(10,-7,1).

13.19. Найти точку Q, симметричную точке Р(-3,2,5) относительно плоскости, проходящей через прямые

13.20. Составить уравнение плоскости, проходящей через прямую перпендикулярно к плоскости 2х-3у-1=0.

13.21. Вычислить кратчайшее расстояние между двумя прямыми:

13.22. Определить, при каком значении D прямая пересекает 1)ось ОХ, 2)ось ОУ, 3)ось ОZ.

13.23. В пучке плоскостей . Найти плоскость, которая 1)проходит через точку М1(1,-2,3), 2)параллельна оси ОХ, 3)параллельна оси ОZ.

Источник

Доказать, что прямая не пересекает отрезка, ограниченного данными точками

Пожалуйста, максимально обоснуйте решение.

Доказать, что прямая, проходящая через вершину B и середину отрезка OC, делит сторону CD на отрезки 2 к 1
Здравствуйте. Наткнулся на вот такую вот задачу. Диагонали параллелограмма ABCD пересекаются в.

Доказать, что прямая параллельна плоскости
Доказать, что прямая (x+1)/2=(y+1)/-1=(z-3)/3 параллельна плоскости 2x+y-z=0, а прямая.

При каких значениях прямая пересекает ось Ox
Помогите, пожалуйста, решить При каких значениях D прямая 4x-6y+7z+D=0; 2x+5y-3z-10=0 пересекает.

Пересекает ли прямая окружность
Есть класс окружность. Нужно создать метод «добавить/удалить прямую сечения». Прямую задаём двумя.

Определить, пересекает ли прямая прямоугольник
Прямоугольник со сторонами, параллельным осям координат, задается координатами концов некоторой.

Определить пересекает ли прямая отрезок
Помогите пожалуйста реализовать с помощью PHP. Задача на логические операторы. Определить.

Определить пересекает ли прямая треугольник
Моё задание звучит так, найти ближайшее расстояние от прямой до треугольника(при этом нужно указать.

Источник

Геометрия/ условия пересикания плоскости отрезком

Alexey, точка на плоскости и нормальный вектор даны для того, чтобы определить уравнение плоскости. Уравнение плоскости — это закономерность, объединяющая все точки одной и той же плоскости. Посмотрите на иллюстрацию. Уравнение плоскости выражает координаты произвольной точки (x,y,z) через координаты нормального вектора (a,b,c) и константу, которую можно вычислить по координатам конкретной точки принадлежащей плоскости. Всё это равно НУЛЮ. Если взять конкретно любую точку, заведомо принадлежащую заданной плоскости, и подставить координаты точки в уравнение плоскости, то результат всегда будет равен нулю.

Не забывайте, что плоскость делит пространство на 2 полупространства. Если подставить в уравнение плоскости координаты точки НЕ принадлежащей плоскости, то: во-первых, результат никогда не будет равен нулю, во-вторых, знак результата однозначно зависит от полупространства, в которое попадёт выбранная точка.

✓ ОТРЕЗОК ПЕРЕСЕКАЕТ ПЛОСКОСТЬ, ЕСЛИ ЕГО КОНЦЫ ПРИНАДЛЕЖАТ РАЗНЫМ ПОЛУПРОСТРАНСТВАМ ОТНОСИТЕЛЬНО ЭТОЙ ПЛОСКОСТИ.

✓ ОТРЕЗОК ПРИНАДЛЕЖИТ ПЛОСКОСТИ, ЕСЛИ ОБА ЕГО КОНЦА ПРИНАДЛЕЖАТ ПЛОСКОСТИ.

Итак:
1. Выведите уравнение плоскости по точке и нормальному вектору.
2. Подставьте в это уравнение координаты каждого из концов отрезка по отдельности.
3. Результаты подстановки перемножьте.
4. Если произведение:
4а) равно 0, то один из концов отрезка принадлежит плоскости. Далее следует проверить, принадлежат ли плоскости оба конца отрезка.
4б) больше нуля, то отрезок целиком находится в одном полупространстве относительно заданной плоскости.
4в) меньше нуля, то отрезок пересекает плоскость. В этом случае придётся вывести уравнение прямой в пространстве заданной через две точки. Далее решаете систему уравнений: уравнение плоскости и уравнение прямой. Координаты точки пересечения отрезка и плоскости одновременно удовлетворяют и уравнению плоскости и уравнению прямой, то есть в обоих случаях подстановка даёт 0.

°√°

• Совет по поиску точки пересечения отрезка с плоскостью.

Вычислите три величины по координатам концов отрезка:
m = Δx, n = Δy, l = Δz.
Подставьте m,n,l в систему параметрических уравнений прямой. В качестве констант возьмите координаты любого конца отрезка.
Все три уравнения подставьте в уравнение плоскости. После упрощения получится уравнение с одним неизвестным — t. Решите его. Подстановкой t в параметрические уравнения найдёте точку пересечения отрезка и плоскости.

НИ ПУХА ВАМ, НИ ПЕРА!
🙂

Alexey, по-моему Вы запутались. Вам следовало дисциплинированно и пунктуально следовать плану.
Попробуем разобраться в вашем примере.

1. Дано: отрезок AB, точка M(3;5;4), нормаль υ(0;1;0).
✓ Плоскость с нормалью υ, содержащая точку M, описывается уравнением

0·x + 1·y + 0·z – (0·3 + 1·5 + 0·4) = 0,

упрощённо y –5 = 0 или y = 5. Получилась плоскость перпендикулярная оси OY и пересекающая её в точке (0;5;0).
*ПОЯСНЕНИЕ*. Уравнение получается из общего a·x + b·y + c·z – (a·Xm + b·Ym + c·Zm) = 0 путём подстановки в него заданных параметров: вектора υ и точки M. Если υ(a;b;c) = υ(0;1;0), то a = 0, b = 1, c = 0. Логично. Так же Xm, Ym, Zm — это координаты точки M, следовательно Xm = 3, Ym = 5, Zm =4. Здесь x, y и z — это неизвестные нам величины. ⟨ПЕРЕНОШУ ДАЛЕЕ⟩

2. Подставлять в полученное уравнение плоскости следует именно координаты точек A и B. Координаты подставляются на место неизвестных величин — переменных x, y и z.
Для точки A имеем: x = 0, y =0, z =0. Подстановка: 0·0 + 1·0 + 0·0 – (0·3 + 1·5 + 0·4) = –5.

✓ ВАЖНО. При подстановке ни в коем случае нельзя приравнивать левую часть уравнения нулю, реальное значение получившегося выражения следует ВЫЧИСЛИТЬ. Значение выражения будет равно нулю ТОЛЬКО в том случае, если подставленный конец отрезка (в примере это точка A) принадлежит заданной плоскости. Если значение выражения отлично от нуля, значит … ⟨ПЕРЕНОШУ ДАЛЕЕ⟩

⟨ПЕРЕНЕСЕНО ИЗ ПРЕДЫДУЩЕГО⟩
Если значение выражения отлично от нуля, значит подставленный конец отрезка НЕ принадлежит заданной плоскости. Вычисленное значение вырвжения следует запомнить, т. к. оно участвует в дальнейших вычислениях.

*ПОЯСНЕНИЕ*. Вам, Alexey, следует запомнить, что именно значение выражения, получаемого путём подстановки координат конкретной точки в уравнение заданной плоскости, определяет, в какое полупространство относительно заданной плоскости попадает заданная точка. Точнее, достаточно одного только знака этого числа (в приведённом выше примере получилось число –5, отрицательное).

Для точки B имеем: x = 1, y =0, z =0. Подстановка: 0·1 + 1·0 + 0·0 – (0·3 + 1·5 + 0·4) = –5. Это число так же не равно 0, значит точка B не принадлежит заданной плоскости. ⟨ПЕРЕНОШУ ДАЛЕЕ⟩

⟨ПЕРЕНЕСЕНО ИЗ ПРЕДЫДУЩЕГО⟩

3. Не напрасно мы запоминали два значения вычисленные выше. Теперь перемножаем их.

✓ Откровенно говоря, достаточно перемножить только знаки (в программе это выражается значениями –1, 0 и +1).

ВЫВОД: полученное произведение строго БОЛЬШЕ НУЛЯ, следовательно весь отрезок AB лежит в одном полупространстве относительно заданной плоскости. В данном примере искать точку пересечения отрезка с плоскостью бессмысленно.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

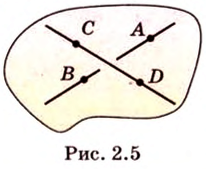
Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

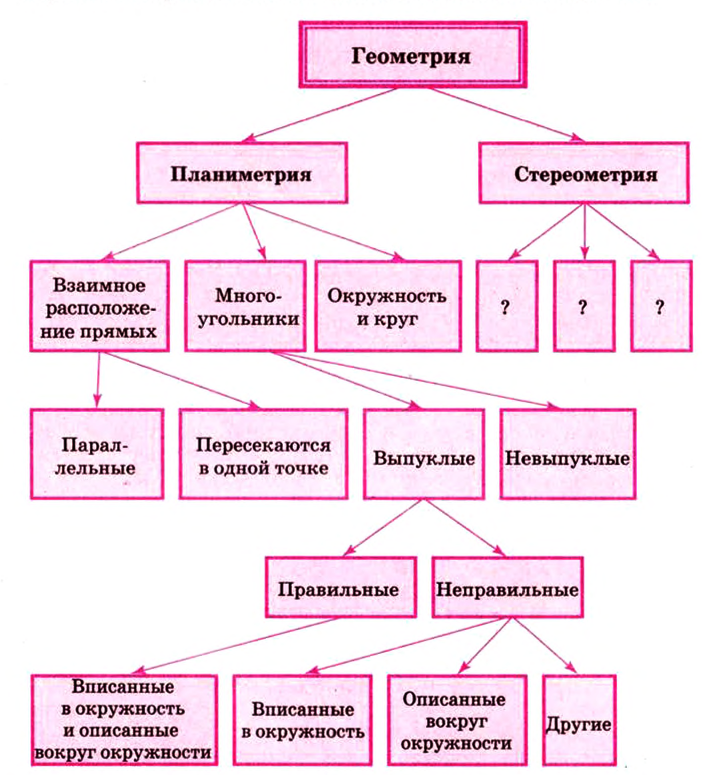
Содержание:

Стереометрия:

Что такое стереометрия

Схематически это выглядит так:

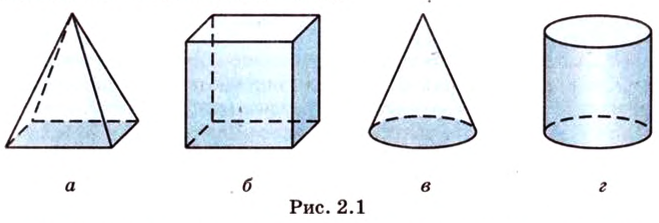
Фигуры, которые изучаются в стереометрии, называются геометрическими или пространственными. На рисунке 2.1 изображены некоторые пространственные фигуры: пирамида, параллелепипед, конус, цилиндр.

Напомним структуру логического построения планиметрии:

В стереометрии рассматривают более одной плоскости. Пространство состоит из бесконечного количества плоскостей, прямых и точек. Поэтому все аксиомы планиметрии имеют место и в стереометрии. Однако при этом некоторые из них приобретают другой смысл. Так, аксиома I, в планиметрии утверждает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Именно в таком понимании эта аксиома применялась в процессе построения геометрии на плоскости. Теперь эта аксиома утверждает вообще существование точек, не лежащих на данной прямой, в пространстве. Из нее непосредственно не вытекает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Это требует уже специального доказательства.

Аксиомы стереометрии

Формулирование некоторых аксиом планиметрии как аксиом стереометрии требует уточнения. Это касается, например, аксиом .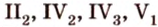

Приведем эти уточнения.

Понятно, что с увеличением количества основных фигур появляются новые аксиомы об их свойствах:

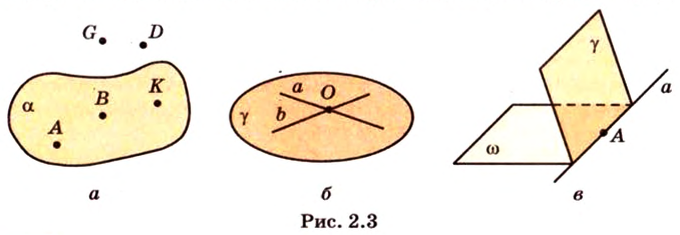
Аксиома 1 указывает на то, что любая плоскость все пространство не исчерпывает. Существуют точки пространства, которые ей не принадлежат.

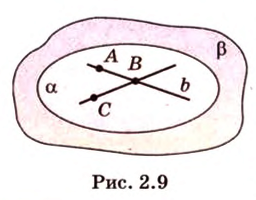
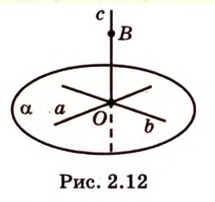
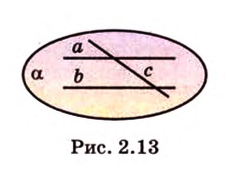
Аксиома 2 утверждает, что две прямые, пересекающиеся в пространстве, всегда определяют одну плоскость. Из аксиомы 3 следует, что если две различные плоскости имеют общую точку, то они имеют множество общих точек, образующих прямую, которая содержит эту точку.

Итак, используя рисунок 2.3, аксиомы можно записать:

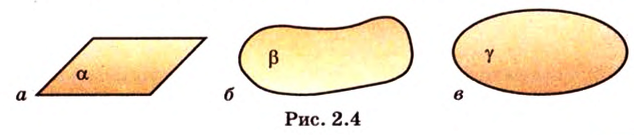
Плоскости изображают по-разному. На рисунке 2.4 показаны некоторые примеры различных изображений плоскостей.

Далее в стереометрии мы будем использовать все определяемые понятия планиметрии, дополнять их новыми, собственно стереометрическими, формулировать и доказывать свойства пространственных фигур.
Как видим, логическое построение планиметрии и стереометрии одинаково, отличаются они лишь некоторым содержанием основных понятий, аксиом, определений, теорем.

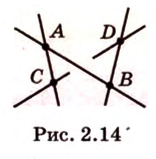
Пример №1

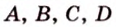
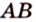
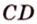
Точки не лежат на одной плоскости. Докажите, что прямые и не пересекаются.

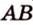
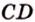
Докажем методом от противного. Допустим, что прямые и пересекаются (рис. 2.5).

Тогда, по аксиоме II₃, через них можно провести плоскость, которой принадлежат эти прямые. Это означает, что точки 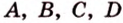также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые и не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.

Следствия из аксиом стереометрии

Проанализировав все сказанное ранее, можно утверждать, что логическое построение геометрии имеет следующий вид:

Важное место в геометрии занимают аксиомы. Они выражают наиболее существенные свойства основных геометрических фигур. Все остальные свойства геометрических фигур устанавливаются рассуждениями, опирающимися на аксиомы или ранее доказанные утверждения, которые опираются на аксиомы. Такие рассуждения называют доказательствами. Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими из них являются утверждения для основных фигур стереометрии. Они называются следствиями из аксиом стереометрии. Рассмотрим теоремы, которые являются следствиями из аксиом стереометрии.

Теорема 1

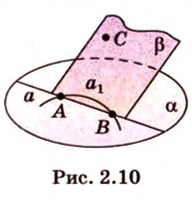
Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.

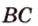
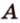
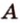
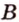
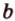
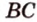
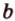
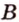
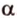
Пусть — данная прямая и — точка, не принадлежащая ей (рис. 2.9). Через точки и проведем прямую . Прямые и различны и пересекаются в точке . По аксиоме II₃ через них можно провести плоскость . Докажем, что она единственная, методом от противного.

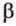
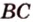
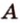
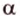
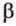
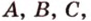
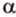
Допустим, что существует другая плоскость , которая содержит прямую и точку . Тогда, согласно аксиоме II4, плоскости и пересекаются по общей прямой, которой принадлежат точки что противоречит условию. Предположение неверно. Плоскость — единственная. Теорема доказана.

Теорема 2
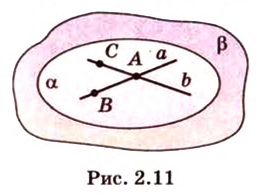
Если две точки прямой принадлежат плоскости, то и вея прямая принадлежит этой плоскости.

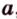
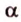
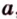
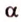
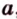
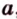
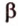
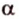
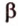
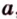
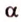
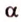
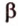
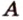
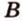
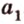
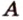
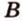
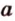
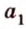
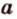
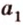
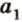
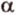
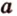
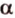
Пусть заданы прямая , плоскость и точки А и В прямой , принадлежащие (рис. 2.10). Выберем точку С, которая не принадлежит прямой . Через точку С и прямую проведем плоскость . Если и совпадут, то прямая принадлежит плоскости . Если же плоскости и различны и имеют две общие точки и , то они пересекаются по прямой , содержащей эти точки. Поэтому через две точки и проходят две прямые и , что противоречит аксиоме принадлежности I₂. Поэтому и — совпадают. Однако поскольку , принадлежит плоскости , то и прямая также принадлежит .

Теорема 3

Через три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

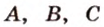
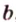
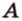
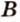
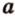
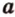
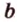
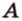
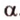
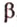
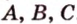
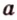
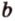
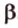
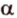
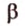
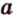
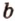
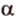
Пусть — заданные точки (рис. 2.11). Проведем через точки и прямую , а через точки и — прямую . Прямые и различны и имеют общую точку . Через них можно провести плоскость . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость , содержащая точки . Тогда, по теореме 2, прямые и принадлежат плоскости . Поэтому плоскости и имеют две общие прямые и , которые пересекаются, что противоречит аксиоме II₃. Итак, плоскость — единственная. Теорема доказана.

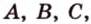
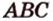
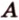
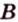
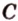
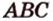
Отметим, если плоскость определена тремя точками, которые не лежат на одной прямой, например то в таком случае пользуются обозначением: (). Читается: «плоскость, заданная точками , и », или сокращенно «плоскость ».

Пример №2

Можно ли через точку пересечения двух данных прямых провести третью прямую, которая бы не лежала с ними в одной плоскости?

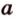
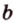
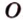
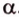
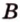
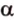
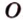
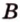
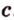
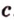
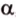
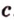
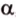
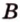
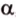
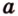
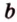
Через прямые и (рис. 2.12), которые имеют общую точку , можно провести плоскость . Возьмем точку , которая не принадлежит . Через точки и проведем прямую . Прямая не лежит на плоскости , так как если бы прямая принадлежала плоскости , то и точка принадлежала бы плоскости . Поэтому через точку пересечения прямых и можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.

Очевидно, что точки плоскости задают прямые, которые будут принадлежать этой самой плоскости. Если же взять точку пересечения двух прямых на плоскости и точку вне плоскости, то через любые две точки пространства можно провести прямую. Эта прямая будет иметь только одну общую точку с плоскостью, а значит, будет ее пересекать.

Пример №3

Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.

Пример №4

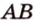
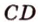
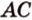
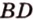
Докажите, что если прямые и не лежат в одной плоскости, то прямые и также не лежат в одной плоскости.

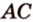
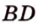
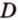
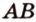
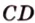
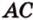
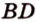
Докажем методом от противного. Допустим, что прямые и лежат в одной плоскости (рис. 2.14). Тогда точки принадлежат этой плоскости, а следовательно, прямые и принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые и не принадлежат одной плоскости, что и требовалось доказать.

Пример №5

Сколько всего существует различных плоскостей, проходящих через прямую и точку в пространстве?

Если в пространстве даны прямая и точка, лежащая на ней, то ими определяется множество плоскостей, поскольку через прямую проходит множество различных плоскостей.
Если же точка не лежит на прямой, то по следствию из аксиом стереометрии такую плоскость можно построить только одну.

Ответ. Бесконечно много или одна.

Взяв вне этой прямой произвольную точку, мы всякий раз будем иметь другую плоскость, не совпадающую с ранее построенной. Таких плоскостей множество.
Через данную точку вне прямой можно провести либо прямую, которая пересекает данную прямую, либо прямую, параллельную данной. Оба случая задают одну плоскость.

Сечения

Анализируя окружающий мир и систематизируя его предметы по форме, мы убеждаемся, что много из них «усечены» или «склеены». Разъединив их, получим поверхность, которую называют их сечением.

С сечениями мы сталкиваемся в разнообразных ситуациях: в быту, в столярничестве, токарстве и т.д. Решением задач на сечения геометрических фигур или других тел занимаются в черчении и конструкторской практике. Сечения выполняют для пространственных геометрических фигур.

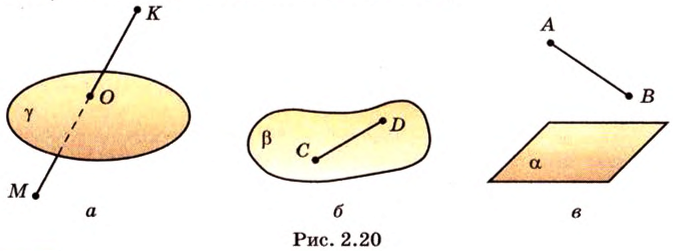
Каждая плоскость разбивает пространство на два полупространства, а концы отрезка могут лежать в различных полупространствах (рис. 2.20, а) относительно некоторой плоскости, на плоскости (рис. 2.20, б) или в одном полупространстве (рис. 2.20, в).

Если ни одна из двух точек не принадлежит плоскости, а отрезок, соединяющий их, имеет с этой плоскостью общую точку, то говорят, что данные точки лежат по разные стороны относительно плоскости, или отрезок пересекает плоскость. Если же как минимум две точки пространственной геометрической фигуры лежат по разные стороны плоскости, то говорят, что плоскость эту фигуру пересекает, такую плоскость называют секущей.

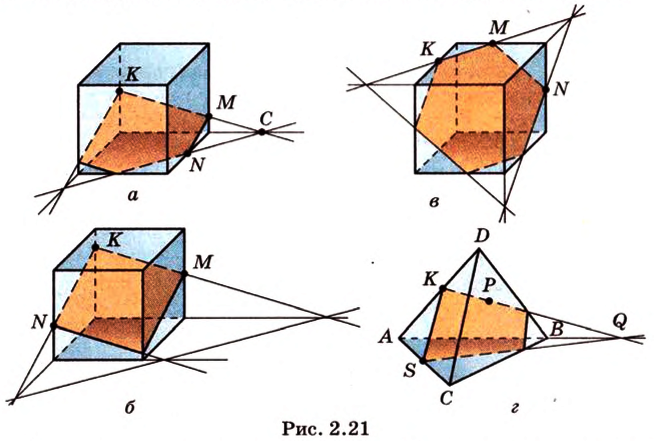
Фигура, которая состоит из всех общих точек геометрической фигуры и секущей плоскости, называется сечением геометрической фигуры. На рисунке 2.21 сечения изображены цветом.

Если плоскость грани многогранника и плоскость сечения имеют две общие точки, то они пересекаются по прямой, проходящей через эти точки. Эту прямую называют линией пересечения данных плоскостей.
Плоскость сечения многогранника имеет общие прямые с плоскостями граней многогранника. Прямую, по которой плоскость сечения пересекает плоскость любой грани многогранника, называют следом плоскости сечения. Следов столько, сколько плоскостей граней пересекает плоскость сечения.

При построении сечения следует помнить:

Рассмотрим примеры построения сечения многогранника секущей плоскостью.

Пример №6

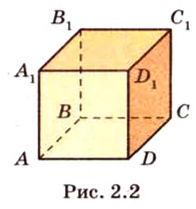
Постройте сечение куба плоскостью, проходящей через середины ребер с общей вершиной.

Построение

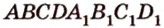
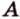
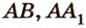
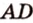
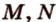
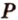
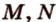
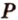
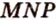
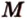
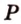
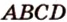
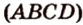
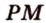
Пусть — заданный куб (рис. 2.22). Выберем одну из вершин, например , являющуюся общей для трех ребер и . Обозначим на этих ребрах точки и соответственно, являющиеся их серединами. Точки и не лежат на одной прямой, а поэтому определяют секущую плоскость (). Точки и — общие точки плоскости сечения и грани , поэтому , — сторона сечения.
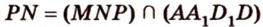
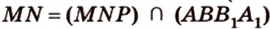
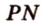
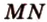
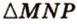
Аналогично и , поэтому и — две другие стороны сечения. Таким образом, — искомое сечение.

Пример №7

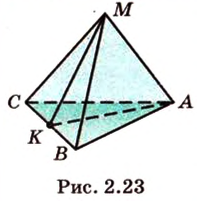
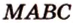
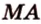
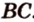
Постройте сечение пирамиды плоскостью, которая проходит через ребро и середину ребра .

Построение

Пример №8

Постройте сечение пирамиды плоскостью, проходящей через три точки, которые лежат соответственно на ребрах , .

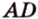
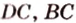
Построение

Рассмотрим случай, когда ни одна из прямых, проходящих через эти точки, не будет параллельна сторонам граней.

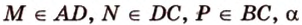
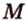
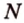
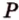
Пусть — секущая плоскость, проходящая через заданные точки , и . Построим сечение, выполняя последовательно шаги:

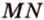
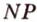
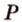
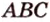
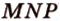
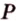
Мы нашли две стороны фигуры сечения: отрезки и (рис. 2.24, а). Точка — общая точка двух плоскостей () и (). Такие плоскости (по аксиоме II₄) пересекаются по прямой, проходящей через точку . Для построения такой прямой нужна вторая точка.

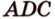
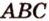
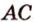
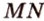
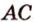
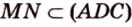
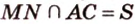
3. Плоскости () и () пересекаются по прямой . по условию не параллельна и , поэтому (рис. 2.24, б).
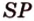
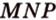
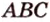
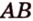
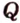
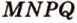
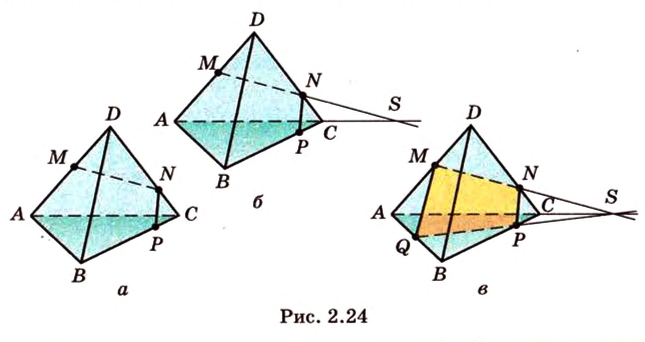
4. Прямая — линия пересечения плоскостей () и (). Пересечение этой прямой с ребром дает точку , которая является вершиной сечения. Таким образом, четырехугольник — искомое сечение (рис. 2.24, в).

Пример №9

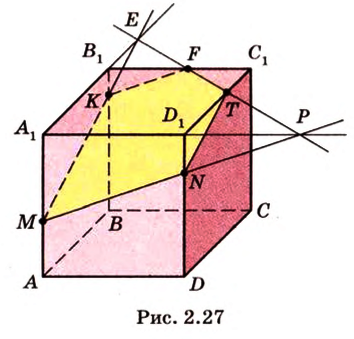
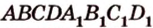
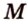
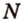
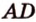
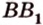
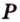
Постройте сечение прямоугольного параллелепипеда плоскостью, проходящей через середины и ребер и и точку пересечения диагоналей грани (рис. 2.25, а).

Построение

Обозначим секущую плоскость 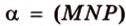. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.

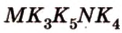
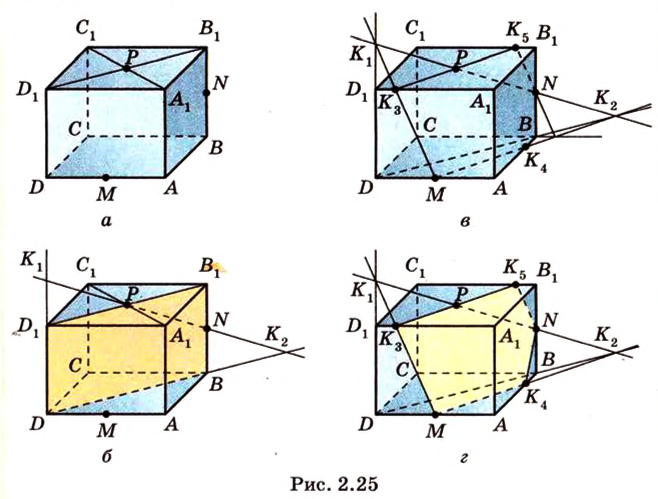
Таким образом, пятиугольник — искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.

Пример №10

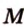
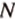
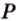
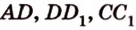
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам .

Построение

Секущая плоскость 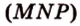) (рис. 2.26).

Пример №11

Постройте сечение куба плоскостью, проходящей через точки К, М, Т, которые принадлежат соответственно ребрам , .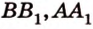

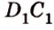
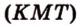
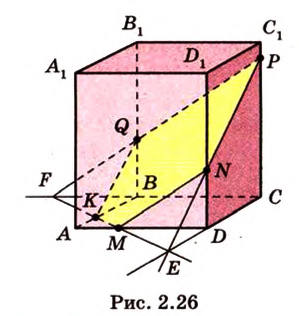
Секущая плоскость (рис. 2.27).

Пример №12

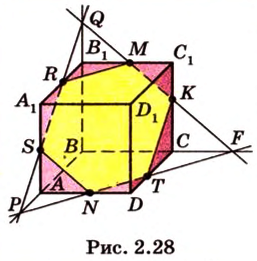
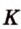
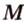
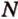
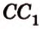
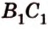
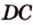
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам ,, .

Построение

Секущая плоскость 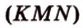(рис. 2.28).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник