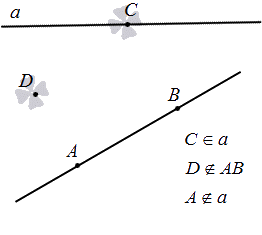
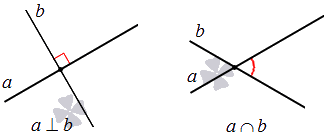
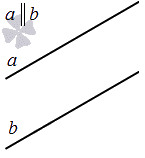
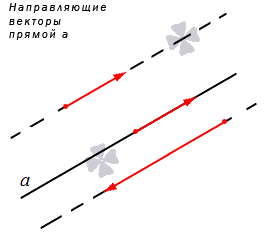
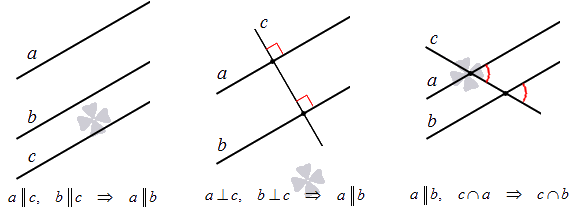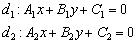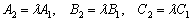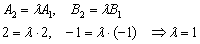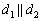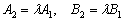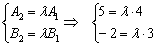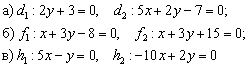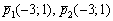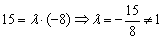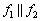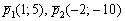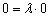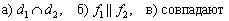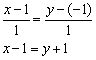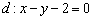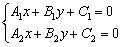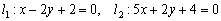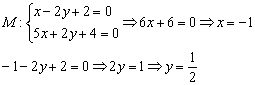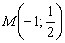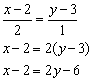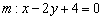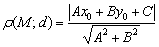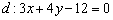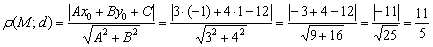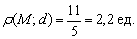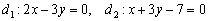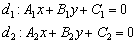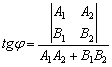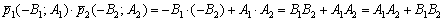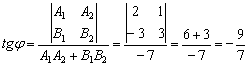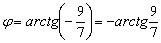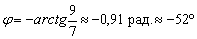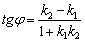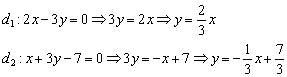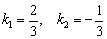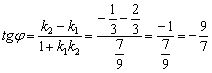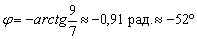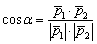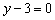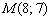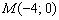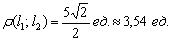доказать что прямые совпадают

О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции ( А ₁В₁ ∩ С ₁D₁ Þ АВ ∩ СD ).

3. Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

Две прямые на плоскости могут быть параллельны.

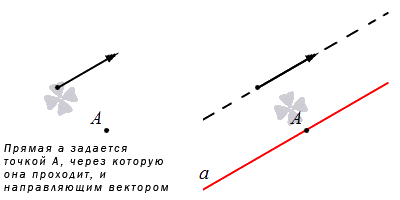
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

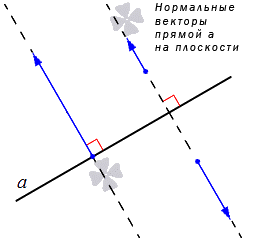
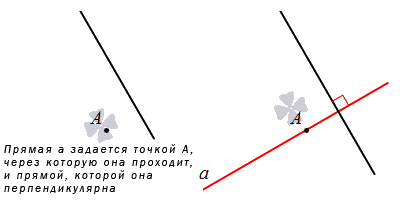
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

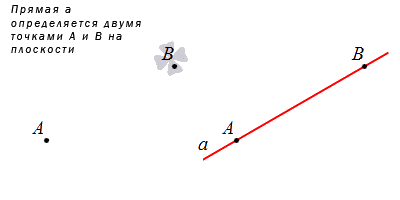
Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

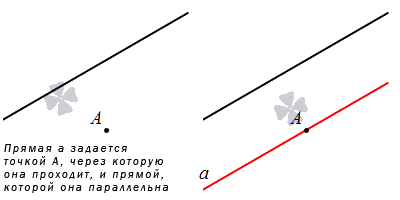
Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

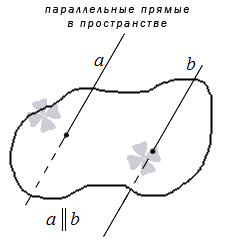
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

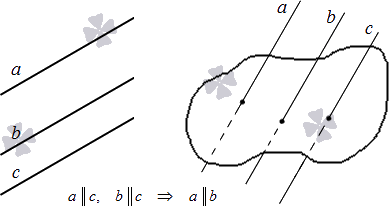
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

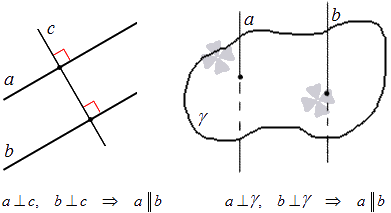
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Простейшие задачи с прямой на плоскости.
Взаимное расположение прямых. Угол между прямыми

Продолжаем рассматривать эти бесконечные-бесконечные прямые. На уроке Уравнение прямой на плоскости мы познакомились с основными видами уравнений, направляющим вектором прямой и её вектором нормали. Данная статья является логическим продолжением темы, и в ней будут разобраны следующие типовые задачи, для опытных путешественников сразу кликабельное оглавление:

О-о-о-о-о… ну и жесть, словно вам сам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.

Взаимное расположение двух прямых

Рассмотрим две прямые, заданные уравнениями в общем виде:

Тот случай, когда зал подпевает хором. Две прямые могут:

2) быть параллельными: ;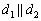

3) или пересекаться в единственной точке: .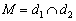

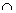
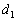
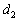
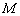
Справка для чайников: пожалуйста, запомните математический знак пересечения , он будет встречаться очень часто. Запись обозначает, что прямая пересекается с прямой в точке .

Как определить взаимное расположение двух прямых?

Начнём с первого случая:

Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

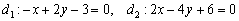
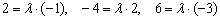
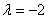
Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.

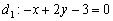
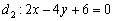
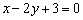
Действительно, если все коэффициенты уравнения умножить на –1 (сменить знаки), и все коэффициенты уравнения сократить на 2, то получится одно и то же уравнение: .

Второй случай, когда прямые параллельны:

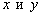
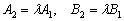
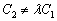
Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных пропорциональны: , но .

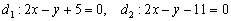
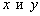
В качестве примера рассмотрим две прямые . Проверяем пропорциональность соответствующих коэффициентов при переменных :

Однако совершенно очевидно, что .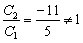

Вывод:

И третий случай, когда прямые пересекаются:

Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных 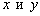НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Так, для прямых 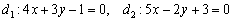составим систему:

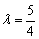
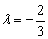
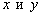
Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность, который мы рассматривали на уроке Понятие линейной (не) зависимости векторов. Базис векторов. Но существует более цивилизованная упаковка:

Выяснить взаимное расположение прямых:

Решение основано на исследовании направляющих векторов прямых:

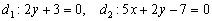
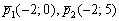
а) Из уравнений найдём направляющие векторы прямых: .

Вычислим определитель, составленный из координат данных векторов: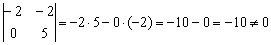
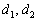
, значит, векторы не коллинеарны и прямые пересекаются.

На всякий случай поставлю на распутье камень с указателями:

1) Если мало что понятно, начните со статьи Векторы для чайников.
2) Если не понятно, как находить направляющие векторы прямых, прошу посетить урок Уравнение прямой на плоскости.
3) Если неясно, причём тут определитель, вам сюда – Понятие линейной (не) зависимости векторов. Базис векторов.

Остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)

б) Найдем направляющие векторы прямых :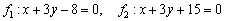

Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.

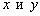
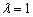
Очевидно, что коэффициенты при переменных пропорциональны, при этом .

Выясним, справедливо ли равенство :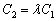

Таким образом,

в) Найдем направляющие векторы прямых :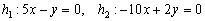

Вычислим определитель, составленный из координат данных векторов: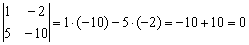
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.

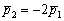
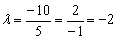
Коэффициент пропорциональности «лямбда» нетрудно усмотреть прямо из соотношения коллинеарных направляющих векторов . Впрочем, его можно найти и через коэффициенты самих уравнений: .

Теперь выясним, справедливо ли равенство 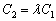. Оба свободных члена нулевые, поэтому:

Полученное значение 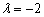удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ:

Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно буквально в считанные секунды. В этой связи не вижу смысла предлагать что-либо для самостоятельного решения, лучше заложим ещё один важный кирпич в геометрический фундамент:

Как построить прямую, параллельную данной?

За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.

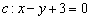
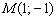
Прямая задана уравнением . Составить уравнение параллельной прямой, которая проходит через точку .

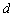
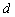
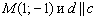
Решение: Обозначим неизвестную прямую буквой . Что о ней сказано в условии? Прямая проходит через точку . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».

Вытаскиваем направляющий вектор из уравнения :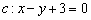

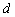
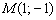
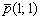
Уравнение прямой составим по точке и направляющему вектору :

Ответ:

Геометрия примера выглядит незатейливо:

Аналитическая же проверка состоит в следующих шагах:

1) Проверяем, что у прямых 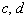один и тот же направляющий вектор (если уравнение прямой не упрощено должным образом, то векторы будут коллинеарны).

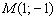
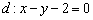
2) Проверяем, удовлетворяет ли точка полученному уравнению .

Аналитическую проверку в большинстве случаев легко выполнить устно. Посмотрите на два уравнения, и многие из вас быстро определят параллельность прямых безо всякого чертежа.

Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница всяких загадок.

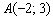
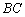
Составить уравнение прямой, проходящей через точку , параллельную прямой , если

Существует рациональный и не очень рациональный способ решения. Самый короткий путь – в конце урока.

С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому рассмотрим задачу, которая хорошо знакома вам из школьной программы:

Как найти точку пересечения двух прямых?

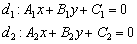
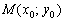
Если прямые пересекаются в точке , то её координаты являются решением системы линейных уравнений

Как найти точку пересечения прямых? Решить систему.

Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.

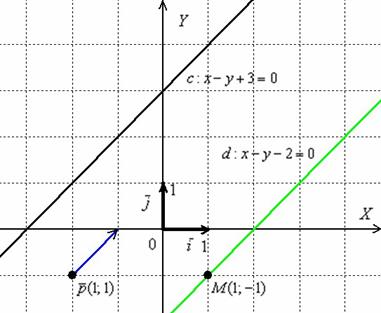
Найти точку пересечения прямых

Решение: Существуют два способа решения – графический и аналитический.

Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа: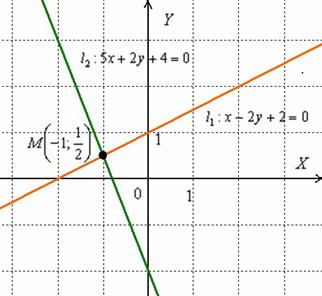

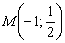
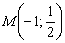
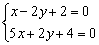
Вот наша точка: . Для проверки следует подставить её координаты в каждое уравнение, они должны подойти и там, и там. Иными словами, координаты точки являются решением системы . По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.

Графический способ, конечно, неплох, но существует заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.

Поэтому точку пересечения 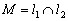целесообразнее искать аналитическим методом. Решим систему:

Для решения системы использован метод почленного сложения уравнений. Чтобы наработать соответствующие навыки, посетите урок Как решить систему уравнений?

Ответ:

Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы.

Найти точку пересечения прямых 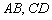в том случае, если они пересекаются.

Это пример для самостоятельного решения. Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что нужно:
1) Составить уравнение прямой .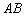
2) Составить уравнение прямой .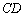
3) Выяснить взаимное расположение прямых .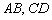
4) Если прямые пересекаются, то найти точку пересечения.

Разработка алгоритма действий типична для многих геометрических задач, и я на этом буду неоднократно заострять внимание.

Полное решение и ответ в конце урока:

Ещё не стоптана и пара башмаков, как мы подобрались ко второму разделу урока:

Перпендикулярные прямые. Расстояние от точки до прямой.
Угол между прямыми

Начнём с типовой и очень важной задачи. В первой части мы узнали, как построить прямую, параллельную данной, а сейчас избушка на курьих ножках развернётся на 90 градусов:

Как построить прямую, перпендикулярную данной?

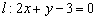
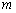
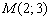
Прямая задана уравнением в декартовой системе координат. Составить уравнение перпендикулярной прямой , проходящей через точку .

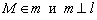
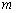
Решение: По условию известно, что . Неплохо бы найти направляющий вектор прямой . Поскольку прямые перпендикулярны, фокус прост:

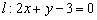
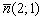
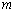
Из уравнения «снимаем» вектор нормали: , который и будет направляющим вектором прямой .

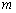
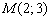
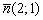
Уравнение прямой составим по точке и направляющему вектору :

Ответ:

Развернём геометрический этюд:

М-да… Оранжевое небо, оранжевое море, оранжевый верблюд.

Аналитическая проверка решения:

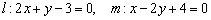
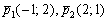
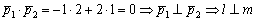
1) Из уравнений вытаскиваем направляющие векторы и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны: .

Кстати, можно использовать векторы нормали, это даже проще.

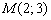
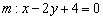
2) Проверяем, удовлетворяет ли точка полученному уравнению .

Проверку, опять же, легко выполнить устно.

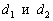
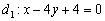
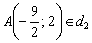
Найти точку пересечения перпендикулярных прямых , если известно уравнение в декартовой системе координат и точка .

Это пример для самостоятельного решения. В задаче несколько действий, поэтому решение удобно оформить по пунктам.

Наше увлекательное путешествие продолжается:

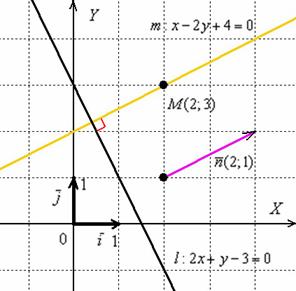
Расстояние от точки до прямой

Перед нами прямая полоса реки и наша задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение по перпендикуляру. То есть, расстояние от точки до прямой – это длина перпендикулярного отрезка.

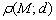
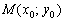
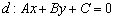
Расстояние в геометрии традиционно обозначают греческой буквой «ро», например: – расстояние от точки «эм» до прямой «дэ».

Расстояние от точки до прямой , заданной в декартовой системе координат, выражается формулой

Найти расстояние от точки 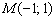до прямой

Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:

Ответ:

Выполним чертёж: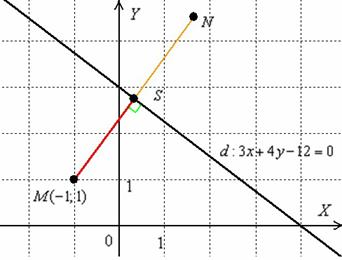

Найденное расстояние от точки до прямой – это в точности длина красного отрезка. Если оформить чертёж на клетчатой бумаге в масштабе 1 ед. = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.

Рассмотрим ещё одно задание по этому же чертежу:

Как построить точку, симметричную относительно прямой?

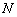
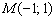
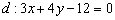
Задача состоит в том, чтобы найти координаты точки , которая симметрична точке относительно прямой . Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:

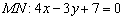
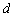
1) Находим прямую , которая перпендикулярна прямой .

2) Находим точку пересечения прямых: .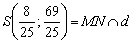

Оба действия подробно разобраны в рамках данного урока.

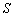
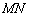
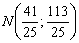
3) Точка является серединой отрезка . Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим .

Не лишним будет проверить, что расстояние 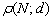тоже равно 2,2 единицам.

Трудности здесь могут возникнуть в вычислениях, но в вышке здорово выручает микрокалькулятор, позволяющий считать обыкновенные дроби. Неоднократно советовал, посоветую и снова.

Как найти расстояние между двумя параллельными прямыми?

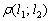
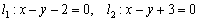
Найти расстояние между двумя параллельными прямыми , заданными в декартовой системе координат.

Это очередной пример для самостоятельного решения. Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце урока, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать.

Угол между двумя прямыми

Что ни угол, то косяк: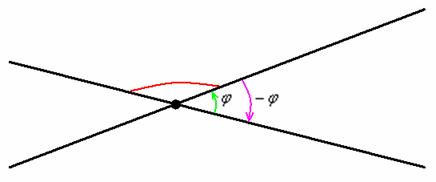

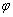
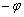
В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом между пересекающимися прямыми. А считается таковым его «зелёный» сосед или противоположно ориентированный «малиновый» угол .

Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4 углов.

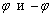
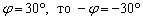
Чем отличаются углы ? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если .

Зачем я это рассказал? Вроде бы можно обойтись и обычным понятием угла. Дело в том, что в формулах, по которым мы будем находить углы, запросто может получиться отрицательный результат, и это не должно застать вас врасплох. Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке).

Как найти угол между двумя прямыми? Существуют две рабочие формулы:

Найти угол между прямыми

Решение и Способ первый

Рассмотрим две прямые, заданные общими уравнениями в декартовой системе координат:

Если прямые не перпендикулярны, то ориентированный угол 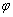между ними можно вычислить с помощью формулы:

Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых:

Если 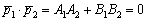, то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.

Исходя из вышесказанного, решение удобно оформить в два шага:

1) Вычислим скалярное произведение направляющих векторов прямых: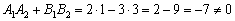
, значит, прямые не перпендикулярны.

2) Угол между прямыми найдём по формуле:

С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса (см. Графики и свойства элементарных функций):

Ответ:

В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора.

Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация: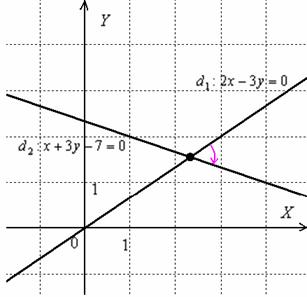

Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи первым номером идёт прямая 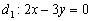и «открутка» угла началась именно с неё.

Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты взять из второго уравнения , а коэффициенты взять из первого уравнения . Короче говоря, начать нужно с прямой .

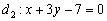
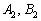
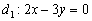
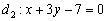
Утаивать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.

Для проверки решения можно взять транспортир и измерить угол.

Способ второй

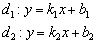
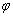
Если прямые заданы уравнениями с угловым коэффициентом (декартовы координаты) и не перпендикулярны, то ориентированный угол между ними можно найти с помощью формулы:

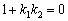
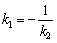
Условие перпендикулярности прямых выражается равенством , откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых: , которая используется, в частности при нахождении уравнения нормали.

Алгоритм решения похож на предыдущий пункт. Но сначала перепишем наши прямые в нужном виде:

Таким образом, угловые коэффициенты:

1) Проверим, будут ли прямые перпендикулярны:
, значит, прямые не перпендикулярны.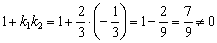

2) Используем формулу:

Ответ:

Второй способ уместно использовать тогда, когда уравнения прямых изначально заданы с угловым коэффициентом. Следует отметить, что если хотя бы одна прямая параллельна оси ординат, то формула не применима вообще, поскольку для таких прямых угловой коэффициент не определён (см. статью Уравнение прямой на плоскости).

Есть и третий способ решения. Идея состоит в том, чтобы вычислить угол между направляющими векторами прямых с помощью формулы, рассмотренной на уроке Скалярное произведение векторов:

Здесь уже речь идёт не об ориентированном угле, а «просто об угле», то есть результат заведомо будет положительным. Загвоздка состоит в том, что может получиться тупой угол (не тот, который нужен). В этом случае придётся делать оговорку, что угол между прямыми – это меньший угол, и из «пи» радиан (не из 180 градусов!) вычитать получившийся арккосинус.

Желающие могут прорешать задачу третьим способом. Но я рекомендую всё-таки придерживаться первого подхода с ориентированным углом, по той причине, что он широко распространён.

Найти угол между прямыми 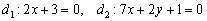, заданными в декартовой системе координат.

Это пример для самостоятельного решения. Попробуйте решить его двумя способами.

Как-то заглохла по ходу дела сказка…. Потому что нет никакого Кащея Бессмертного. Есть я, причём, не особо запаренный. Если честно, думал, статья значительно длиннее выйдет. Но все равно возьму недавно приобретенную шапочку с очками и пойду купаться в сентябрьской озёрной воде. Отлично снимает усталость и негативную энергетику.

И помните, Бабу-Ягу никто не отменял =)

Пример 3: Решение: Найдём направляющий вектор прямой :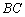

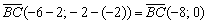
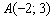
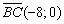
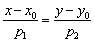
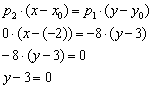
Уравнение искомой прямой составим по точке и направляющему вектору . Так как одна из координат направляющего вектора нулевая, уравнение перепишем в виде:

Ответ:

Пример 5: Решение:
1) Уравнение прямой составим по двум точкам :

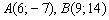
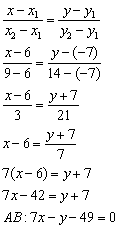
2) Уравнение прямой составим по двум точкам :

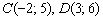
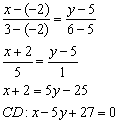
3) Соответствующие коэффициенты при переменных 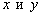не пропорциональны: , значит, прямые пересекаются.
4) Найдём точку :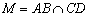

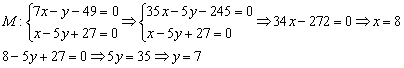
Примечание: здесь первое уравнение системы умножено на 5, затем из 1-го уравнения почленно вычтено 2-е.
Ответ:

Пример 7: Решение:
1) Найдём нормальный вектор прямой: .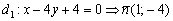
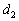
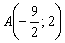
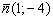
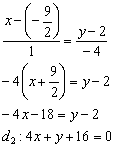
2) Составим уравнение прямой по точке и направляющему вектору :

3) Найдём точку пересечения прямых :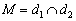

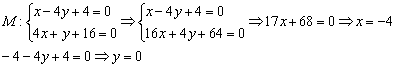
Примечание: второе уравнение умножено на 4, затем уравнения сложены почленно.
Ответ:

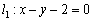
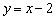
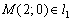
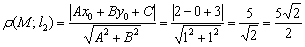
Пример 9: Решение: Расстояние между параллельными прямыми найдём как расстояние от точки до прямой. Для этого достаточно найти одну точку, принадлежащую любой из прямых. В целях удобного подбора точки перепишем уравнение в виде уравнения с угловым коэффициентом: . Точка . Вычислим расстояние:

Последним действием числитель и знаменатель умножен на 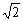– чтобы избавиться от иррациональности в знаменателе.
Ответ:

Пример 11: Решение:
Способ первый
1) Вычислим скалярное произведение направляющих векторов прямых: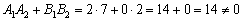
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы: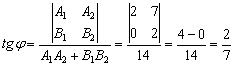

Таким образом: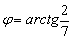

Ответ: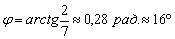
Способ второй применить нельзя, так как прямая 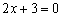параллельна оси ординат, и её угловой коэффициент не определён.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник