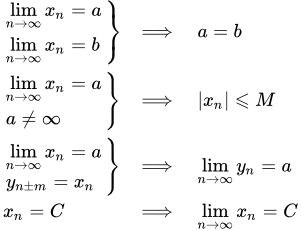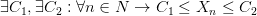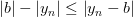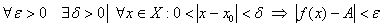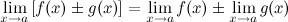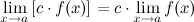доказать что сходящаяся последовательность ограничена

Основные свойства конечных пределов последовательностей

Свойства и теоремы

Свойство окрестности сходящейся последовательности
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Доказательство ⇓

Теорема единственности предела числовой последовательности
Если последовательность имеет предел, то он единственный.
Доказательство ⇓

Теорема об ограниченности последовательности, имеющей конечный предел
Если последовательность имеет конечный предел, то она ограничена.
Доказательство ⇓

Влияние конечного числа элементов на сходимость
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Доказательство ⇓

Доказательство свойств и теорем

При доказательстве свойств, мы будем использовать определение предела последовательности:
.

Свойство окрестности сходящейся последовательности

Все свойства ⇑ Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Тогда первые N элементов последовательности могут находиться где угодно. То есть за пределами окрестность могут находиться не более N элементов последовательности – конечное число или пустое множество.

Первая часть доказана.

Пусть теперь за пределами любой окрестности точки a находится конечное число элементов последовательности или пустое множество. Пусть N есть наибольший номер элемента, находящегося за пределами окрестности. Тогда все элементы последовательности с номерами принадлежат этой окрестности. Это означает, что точка a является пределом последовательности.

Свойство окрестности последовательности, не сходящейся к числу a

Теорема единственности предела числовой последовательности

Все свойства ⇑ Если последовательность имеет предел, то он единственный.

Теорема об ограниченности последовательности, имеющей конечный предел

Все свойства ⇑ Если последовательность имеет конечный предел, то она ограничена.

Теорема о пределе постоянной последовательности

Влияние конечного числа элементов на сходимость

Все свойства ⇑ Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.

Хотя здесь мы рассматриваем только конечные пределы, но доказательство этой теоремы повторяется один в один, если включить в рассмотрение и бесконечные пределы. Поэтому рядом с формулами, применимыми только для конечных пределов, мы будем приводить универсальные формулы, пригодные как для конечных, так и для бесконечных пределов. Их мы будем помечать звездочкой. При первом чтении раздела их можно пропустить.

Тем самым мы доказали, что добавление или удаление первых элементов не влияет на сходимость последовательности. Докажем, что изменение первых m элементов также не влияет на сходимость. Для доказательства удалим первые m элементов у исходной последовательности. Получим промежуточную последовательность, сходимость которой такая же, как у исходной. Затем добавим в промежуточную последовательность первые m элементов с произвольными значениями. Получим последовательность, у которой, по отношению к исходной, изменены первые m элементов. Сходимость такой последовательности такая же как и у промежуточной, а поэтому такая же как и у исходной.

Источник

Сходящиеся последовательности

Последовательность, у которой существует предел, называется сходящейся. Последовательность не являющаяся сходящейся называется расходящейся.

В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.

Можно, также, дать еще одно определение сходящейся последовательности: Последовательность называется сходящейся, если существует такое число а, что для любого положительного числа e можно указать номер N такой, что при n³ N все элементы x n этой последовательности удовлетворяют неравенству:

Некоторые свойства сходящихся последовательностей:

ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.

ТЕОРЕМА: Сходящаяся последовательность ограничена.

Доказательство: Пусть — сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:

ТЕОРЕМА: Сумма сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей <х n >и .

Доказательство: Пусть а и b – соответственно пределы последовательностей <х n >и . Тогда:

ТЕОРЕМА: Разность сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей <х n >и .

Доказательство: Пусть а и b – соответственно пределы последовательностей <х n >и .Тогда:

ТЕОРЕМА: Произведение сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей <х n >и .

ЛЕММА: Если последовательность сходится и имеет отличный от ноля предел b, то, начиная с некоторого номера, определена последовательность , которая является ограниченной.

ТЕОРЕМА: Частное двух сходящихся последовательностей и при условии, что предел отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .

.

Так как последовательность ограничена, а последовательность бесконечно мала, то последовательность бесконечно малая. Теорема доказана.

Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.

ТЕОРЕМА: Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравентству x n³ b (x n£ b), то и предел а этой последовательности удовлетворяет неравенству а³ b (a£ b).

Элементы сходящейся последовательности могут удовлетворять строгому неравенству x n >b, однако при этом предел а может оказаться равным b. Например, если x n =1/n, то x n >0, однако .

.

.

Следствие 2: Если все элементы сходящейся последовательности находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте.

Это выполняется, так как а£ x n£ b, то a£ c£ b.

Итак, мы показали неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.

, и того, что .

(m, n = 1, 2, 3, … ),

,…

должна либо расходиться к , причем предел этой последовательности будет равен ее нижней грани.

,

тогда существует конечный предел

,

(n = 1, 2, 3, … ).

(*)

сходится, ибо в силу неравенства (*) он мажорируется сходящимся рядом:

запишем целое число n по двоичной системе:

.

Применяя теорему (1) для данных:

s 0 =0, s 1 =, s m-1 =, s m =, …, p n0 =0, p n1 =, …, p n, m-1 =,

, p n, m+1 =0, …,

заключаем, что . Наконец, в силу (*) имеем:

.

Если общий член ряда, не являющегося ни сходящимся, ни расходящимся в собственном смысле, стремится к нулю, то частичные суммы этого ряда расположены всюду плотно между их нижним и верхним пределами lim inf и lim sup.

Разобьем числовую прямую на l интервалов точками

.

Существуют в сколь угодно большом удалении конечные последовательности , произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу.

, …

заполняет замкнутый интервал (длина которого равна нулю, если эта последовательность стремится к пределу).

Числовая последовательность, стремящаяся к , имеет наименьший член.

Какое бы число мы ни задали, слева от него будет находиться лишь конечное число членов последовательности, а среди конечного множества чисел существует одно или несколько наименьших.

Сходящаяся последовательность имеет либо наибольший член, либо наименьший, либо и тот и другой.

При совпадении верхней и нижней граней рассматриваемой последовательности теорема тривиальна. Пусть поэтому они различны. Тогда по крайней мере одна из них отличается от предела последовательности. Она и будет равна наибольшему, соответственно наименьшему, члену последовательности.

Пусть числовые последовательности

обладают тем свойством, что

, .

Тогда существует бесконечно много номеров n, для которых одновременно выполняются неравенства

l n s n >l n-1 s n-1, l n s n >l n-2 s n-2, … l n s n >l 1 s 1,

Будем называть l m “выступающим” членом последовательности, если l m больше всех последующих членов. Согласно предположению в первой последовательности содержится бесконечно много выступающих членов; пусть это будут:

,…

,

(*)

отсюда заключаем, что

Если числовая последовательность ,… стремится к и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³ 1, что n отношений

все не больше А, а бесконечное множество отношений

,…

Имеем . Пусть минимум последовательности

u=1, 2, …, n; v=1, 2, 3, …; n=0 исключено в силу предложений относительно А.

.

.

,

Пусть, далее, l 1 >A>0. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства

.

Если А® 0, то также n® 0.

Тогда . Последовательность

все положительны: коль скоро А меньше наименьшего из них, соответствующий А номер n больше или равен s. Точки (n, L n ) должны быть обтянуты теперь бесконечным выпуклым сверху полигоном.

Источник

Ограниченность сходящейся последовательности

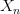
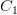
Последовательность называется ограниченной снизу, если существует такое число , что все члены последовательности удовлетворяют условию , т. е.:

Последовательность 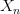называется ограниченной сверху, если:

Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, т. е. последовательность 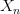называется ограниченной, если:

это можно записать и так:

Таким образом, последовательность называют ограниченной, если множество ее значений ограничено.

Теорема: ( об ограниченности сходящейся последовательности)

Если последовательность имеет предел, то она ограничена.

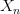
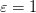
Пусть последовательность имеет предел, равный а. По определению предела для найдем номер N такой, что при всех имеет место неравенство . Так как модуль суммы не превосходит суммы модулей, то:

.

Поэтому при всех выполняется неравенство:

.

Положим , тогда при всех , т. е. последовательность ограничена.

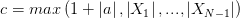
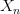
Замечание: В силу предыдущей теоремы всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся! Например, последовательность ограничена, но не является сходящейся.

Замечание: Если условие не выполняется, т. е.

,

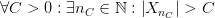
то говорят, что последовательность 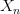не ограничена.

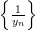
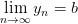
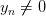
Пример: Доказать, что последовательность является ограниченной, если , и , для всех .

Так как , то . По заданному числу в силу определения предела последовательности найдется номер такой, что:

.

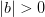
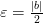
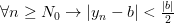
Используя неравенство для модуля разности

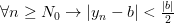
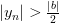
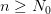
и неравенство , получаем , откуда . И поэтому для всех справедливо неравенство .

Пусть C = max , для всех выполняется неравенство , т. е. – ограниченная последовательность.

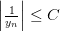
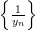
8 Основные свойства сходящихся последовательностей.

Свойства сходящихся последовательностей:

Основные свойства сходящихся последовательностей

1. Если все элементы бесконечно малой последовательности <х_n> равны одному и тому же числу с, то с = 0.

2. Сходящаяся последовательность имеет только один предел.

3. Сходящаяся последовательность ограничена.

4. Сумма (разность) сходящихся последовательностей <х_n> и <у_n> есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей <х_n> и <у_n>.

5. Произведение сходящихся последовательностей <х_n> и <у_n> есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей <х_n> и <у_n>

6. Частное двух сходящихся последовательностей <х_n> и <у_n> при условии, что предел последовательности <у_n>отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей <х_n> и <у_n>.

7. Если элементы сходящейся последовательности <х_n> удовлетворяют неравенству x_n ≥ b (х_n ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ b (а ≤ b).

8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность.

9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Справедлива следующая теорема (основная теорема теории пределов): если то: ; ; при условии, что b ≠ 0 и для всех n.

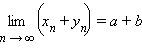
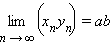
9 Подпоследовательности и их пределы. Лемма больцано-вейерштрасса.

Подпоследовательности

Определение.

Пусть задана некоторая последовательность < > и

есть строго возрастающая последовательность натуральных чисел.Тогда последовательность

называется подпоследовательностью последовательности < >.

Пример.
Пусть задана последовательность

Запишем некоторые ее подпоследовательности:

;

;

;
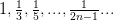
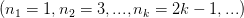
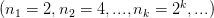
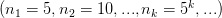
Но последовательность

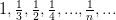
уже не является подпоследовательностью последовательности .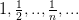

Определение.
Будем писать

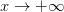
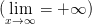
и говорить, что последовательность < > стремится к плюс бесконечности, если для каждого числа найдется номер , такой что при любом
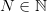
Аналогично даются определения для случая ,

Теорема Больцано — Вейерштрасса, или лемма Больцано — Вейерштрасса о предельной точке — фундаментальная теорема математического анализа, гласящая, что из любой ограниченной последовательности точек пространства 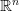можно выделитьсходящуюся подпоследовательность. Т. Б. — В., используется при доказательстве многих теорем анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема названа в честь чешского математикаБернарда Больцано и немецкого математика Карла Вейерштрасса, которые независимо друг от друга вывели ее формулировку и доказательство.

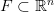
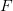
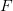
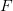
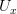
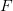
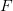
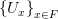
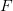
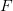
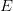
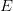
Формулировка.Любое бесконечное ограниченное множество имеет по крайней мере одну предельную точку. Доказательство. Пусть множество является бесконечным и ограниченным множеством. Предположим, что оно не имеет предельных точек. Следовательно, оно является замкнутым. Поскольку еще и ограничено, то, по теореме Гейне – Бореля, компактно. Для каждой точки построим такую окрестность , в которой нет других точек из , кроме (если бы для какой-то точки такой окрестности не было, то эта точка была бы предельной для ). Тогда семейство образуетоткрытое покрытие компактного множества . Пользуясь компактностью , выберем из него некое конечное подпокрытие, иными словами. конечный набор шаров, в каждом из которых содержится лишь по одной точке из множества . Но это противоречит тому, что множество бесконечно.
Замечание. Предельная точка, существование которой утверждается в данной теореме, вообще говоря, не обязана принадлежать множеству .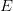

10 Определение пределов функции по коши и гейне.

Предел функции по Гейне: число называется пределом функции в точке , если для любой последовательности точек (принадлежащих и отличных от ), которая сходится к точке , соответствующая последовательность значений функции сходится к .

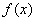
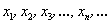
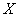
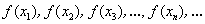
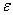
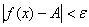
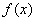
Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность). По мотивам предыдущего параграфа, запись означает, чтонекоторое значение функции находится внутри «эпсилон»-окрестности.

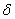
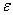
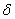
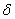
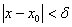
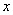
Теперь найдём -окрестность, которая соответствует заданной -окрестности(мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз). Обратите внимание, что значение выбираетсяпо длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определенииважен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши: число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой),существует -окрестность точки , ТАКАЯ, что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки).

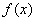
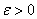
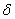
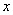
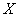
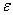
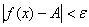
Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая 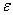-окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание: если вам потребуется сформулировать только определение по Гейне или только определение по Коши, пожалуйста, не забывайте о существенномпредварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки ». Я обозначил это единожды в самом начале и каждый раз не повторял.

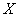
11 Свойства пределов функции.

1° Предел суммы/разности двух функций равен сумме/разности их пределов:

2° Предел произведения двух функций равен произведению их пределов:

3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

4° Константу можно выносить за знак предела:

5° Предел степени с натуральным показателем равен степени предела:

Источник