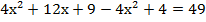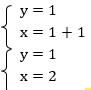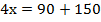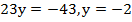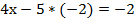доказать что выражение кратно 6

Доказательство кратности и уравнение

Существует обратная задача – разложить многочлен на множители, она решается также с помощью формул сокращенного умножения.

Пример 6: доказать что число кратно 25:

Очевидно, что если мы будем выполнять все вычисления, это будет сложно и долго, но если заметить формулу, то работа значительно упрощается. Итак, мы видим разность кубов. Распишем выражение:

В результате преобразований мы получили выражение, один из множителей которого равен 25, очевидно, что это выражение кратно 25.

Пример 7: решить уравнение:

Напомним, что решить уравнение – означает найти такие значения х, которые обращают выражение в верное числовое равенство. Распишем в уравнении квадрат суммы и разность квадратов:

Соберем неизвестные слева, а свободные члены справа и приведем подобные:

Из полученного элементарного уравнения найдем значение х:

Запишем еще несколько формул, которые можно вывести:

– куб суммы (разности)

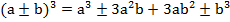
Чтобы вывести данные формулы, нужно выполнить умножение скобок, и вы убедитесь в их справедливости.

Итоги урока

Вывод: мы рассмотрели формулы сокращенного умножения, записали вид основных из них и некоторые доказали. Мы рассмотрели примеры различной сложности, чтобы окончательно закрепить данный материал.

1. Преобразовать выражение в многочлен:

а) (а – 2)(а + 2); б) (7а + 8в)²; в) (с³ – 0,1)².

2. Решить уравнение:

3. Упростить выражение и найдите его значение:

Урок 5:Повторение. Разложение многочленов на множители.

На данном уроке мы вспомним все изученные методы разложения многочлена на множители, рассмотрим примеры к ним.

1. Методы разложения многочленов на множители.

Напомним, что многочлен есть алгебраическая сумма одночленов, а одночлен – это произведение чисел и степеней.

Вспомним способы разложения многочлена на множители.

1. В каждом члене многочлена может быть общий множитель, отсюда первый способ – метод вынесения общего множителя за скобки, то есть такого множителя, который присутствует во всех членах многочлена. Рассмотрим пример 1, вынесем общий множитель за скобки, для этого определим, какие переменные представлены во всех членах, и вынесем их в минимальной степени:

;

Напомним, что, перемножив вынесенный множитель на скобку, можно проверить правильность вынесения.

В обоих членах есть скобка , в одном в первой, а в другом во второй степени, вынесем минимальную ее степень – первую:

2. Метод группировки. Не всегда в многочлене можно вынести общий множитель. В таком случае нужно его члены разбить на группы таким образом, чтобы в каждой группе можно было вынести общий множитель, и постараться разбить так, чтобы после вынесения множителей в группах появился общий множитель у всего выражения, и можно было бы продолжить разложение. Рассмотрим пример 3:

;

Сгруппируем первый член со вторым, третий с четвертым и вынесем общие множители в группах:

У выражения появился общий множитель. Вынесем его:

;

3. Применение формул сокращенного умножения. Рассмотрим пример 4:

Мы расписали заданный многочлен по известной формуле разности кубов.

Комментарий: мы увидели в заданном многочлене формулу суммы кубов и разложили его.

4. Метод выделения полного квадрата. Он базируется на формулах квадрата суммы и квадрата разности. Напомним их:

– формула квадрата суммы (разности);

Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Рассмотрим пример 6:

;

Итак, первое выражение – это , а второе должно быть , но не хватает удвоенного произведения. Прибавим и вычтем его:

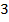
Свернем полный квадрат разности:

;

Преобразуем полученное выражение, применяя формулу разности квадратов, напомним, что разность квадратов двух выражений есть произведение суммы на их разность:

;

Напомним, что, перемножив скобки, можно проверить правильность разложения.

Подведение итогов урока

Вывод: мы вспомнили все изученные методы разложения многочленов на множители и рассмотрели примеры. Вспомнили определение и некоторые свойства алгебраических дробей, решили несколько типовых задач, с ними связанных.

1. Вынести общий множитель за скобки:

а) 8х – 8у; б) 5ху – 7х; в) 25х³ – 10х² + 5х;

2. Решить уравнение:

а) (7х – 10)(х + 5) = 0; б) 12у² – 60у = 0; в) х³ + х² – 4х – 4 = 0.

3. Докажите, что выражение:

а) 5¹³ – 5¹¹ делится на 24; б) 125³ + 625² делится на 6.

4. Разложите на множители способом группировки:

а) 3(а + с) + х(а + с); б) 6х – 6у + ах – ау;

Урок 6: Повторение. Сис­те­мы двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми.

1. Определение системы уравнений с двумя переменными

На­пом­ним, что из себя пред­став­ля­ет си­сте­ма двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми. Это си­сте­ма вида:

Из пер­во­го урав­не­ния можно по­лу­чить ли­ней­ную функ­цию, в слу­чае если : . Гра­фик дан­но­го урав­не­ния – пря­мая линия.

Bто­рое ли­ней­ное урав­не­ние:

, из него также можно по­лу­чить ли­ней­ную функ­цию, при усло­вии, что : . Гра­фик дан­но­го урав­не­ния – также пря­мая линия.

За­пи­шем си­сте­му в дру­гом виде:

Мы знаем, что мно­же­ством ре­ше­ний пер­во­го урав­не­ния яв­ля­ет­ся мно­же­ство точек, ле­жа­щих на со­от­вет­ству­ю­щей ему пря­мой, ана­ло­гич­но и для вто­ро­го урав­не­ния мно­же­ство ре­ше­ний – это мно­же­ство точек на дру­гой пря­мой. Две пря­мые могут пе­ре­се­кать­ся – и тогда у си­сте­мы будет един­ствен­ное ре­ше­ние, един­ствен­ная пара чисел х и у будет удо­вле­тво­рять од­но­вре­мен­но обоим урав­не­ни­ям. Это про­ис­хо­дит, если . Две пря­мые также при неко­то­рых зна­че­ни­ях чис­лен­ных па­ра­мет­ров могут быть па­рал­лель­ны, в таком слу­чае они ни­ко­гда не пе­ре­се­кут­ся и не будут иметь ни одной общей точки, зна­чит в этом слу­чае си­сте­ма не будет иметь ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия: и . Кроме того, две пря­мые могут сов­па­дать, и тогда каж­дая точка будет ре­ше­ни­ем обоих урав­не­ний, а зна­чит си­сте­ма будет иметь бес­чис­лен­ное мно­же­ство ре­ше­ний. Для этого долж­ны вы­пол­нять­ся усло­вия: и .

2. Спо­соб под­ста­нов­ки

На дан­ном урав­не­нии можно про­де­мон­стри­ро­вать сразу несколь­ко спо­со­бов ре­ше­ния си­стем урав­не­ний.

1 спо­соб – спо­соб под­ста­нов­ки: вы­ра­зим во вто­ром урав­не­нии х и под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

Под­ста­вим най­ден­ное зна­че­ние у во вто­рое урав­не­ние и най­дем зна­че­ние х:

3. Спо­соб ал­геб­ра­и­че­ско­го сло­же­ния

2 спо­соб – спо­соб ал­геб­ра­и­че­ско­го сло­же­ния: вы­пол­ним сло­же­ние урав­не­ний:

Из по­лу­чен­но­го урав­не­ния най­дем х:

Те­перь вы­чтем из пер­во­го урав­не­ния си­сте­мы вто­рое:

Таким об­ра­зом, мы по­лу­чи­ли ре­ше­ние си­сте­мы двумя спо­со­ба­ми, и это ре­ше­ние – точка с ко­ор­ди­на­та­ми (2; 1).

4. Си­сте­мы урав­не­ний с одним ре­ше­ни­ем

В дан­ном слу­чае удоб­нее при­ме­нить спо­соб ал­геб­ра­и­че­ско­го сло­же­ния, вы­чтем из вто­ро­го урав­не­ния пер­вое. По­лу­ча­ем:

Под­ста­вим зна­че­ние у во вто­рое урав­не­ние и най­дем х:

В дан­ной си­сте­ме нет пе­ре­мен­ных с оди­на­ко­вы­ми ко­эф­фи­ци­ен­та­ми, но мы можем их урав­нять са­мо­сто­я­тель­но, для этого вы­пол­ним пре­об­ра­зо­ва­ния:

Вы­пол­ним сло­же­ние урав­не­ний:

Под­ста­вим по­лу­чен­ное зна­че­ние у в пер­вое урав­не­ние и опре­де­лим зна­че­ние х:

5. Си­сте­мы, име­ю­щее бес­ко­неч­ное мно­же­ство или не име­ю­щие ре­ше­ний

Раз­де­лим вто­рое урав­не­ние на два:

Вы­чтем из пер­во­го урав­не­ния вто­рое:

Оче­вид­но, что по­лу­чен­ное вы­ра­же­ние не за­ви­сит от зна­че­ний пе­ре­мен­ных си­сте­мы и не яв­ля­ет­ся вер­ным чис­ло­вым ра­вен­ством, зна­чит, си­сте­ма не имеет ре­ше­ний. В дан­ном слу­чае ре­ко­мен­ду­ет­ся гра­фи­че­ски до­ка­зать, что си­сте­ма не имеет ре­ше­ний, для этого из урав­не­ний за­пи­сать ли­ней­ные функ­ции, по­стро­ить их и по­ка­зать, что пря­мые па­рал­лель­ны.

Оче­вид­но, что, если раз­де­лить вто­рое урав­не­ние на два, по­лу­чим пер­вое урав­не­ние:

Мы по­лу­чи­ли два оди­на­ко­вых урав­не­ния, зна­чит, чтобы до­ве­сти ре­ше­ние си­сте­мы до конца, можем оста­вить одно: ; это ли­ней­ное урав­не­ние с двумя пе­ре­мен­ны­ми, гра­фик его – пря­мая линия, и оно имеет бес­чис­лен­ное мно­же­ство ре­ше­ний, а зна­чит и си­сте­ма имеет бес­чис­лен­ное мно­же­ство ре­ше­ний. Чтобы за­пи­сать ре­ше­ния, вы­ра­зим у: , таким об­ра­зом, дадим ответ: х – любое число,

Гра­фи­че­ская ил­лю­стра­ция (рис. 1):

6. Под­ве­де­ние ито­гов урока

Вывод: мы рас­смот­ре­ли си­сте­мы двух ли­ней­ных урав­не­ний с двумя пе­ре­мен­ны­ми, ва­ри­ан­ты и спо­со­бы их ре­ше­ния. Мы вспом­ни­ли неко­то­рые тер­ми­ны, по­ня­тия и свой­ства и ре­ши­ли при­ме­ры для за­креп­ле­ния тех­ни­ки.

1. Решите систему тремя способами: сложением, подстановки, графическим:

2. Сколько решений имеет система:

3. Решите систему любым способом:

Урок 7:Алгебраические дроби. Арифметические операции над алгебраическими дробями.Основные понятия.

На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется по части торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.

1. Определение и примеры алгебраических дробей

Рациональные выражения делятся на целые и дробные выражения.

Определение.Рациональная дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.

Примерырациональных выражений: – дробные выражения; – целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя – .

Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Алгебра

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Понятие делимости и ее основные свойства

Напомним суть операции деления. Она является обратной для операции умножения. Пусть есть три числа, a, b и c, причем для них справедливо соотношение

В таком случае говорят, что a является произведением b и c. Тогда результатом деления числа a на b называют число с.

Если в результате деления числа а на b получилось целое число с, то говорят, что а делится на b.

Так, число 30 делится на 6, потому что при делении 30 на 6 получается целое число 5:

Иногда в математике используют выражение «делится нацело». Оно означает тоже самое, что и просто слово «делится». Например, 81 делится нацело на 3:

Порою в математике используют чуть более сложное определение делимости:

Видно, что оно похоже на определение операции деления. Его удобно использовать при доказательстве некоторых свойств делимости.

Понятие делимости определено только для целых чисел. Например, при делении 12,5 на 2,5 получается целое число:

однако никто не говорит, что 12,5 делится на 2,5.

Если число а делится на b, то b называют делителем числа a, а также говорят, что а – кратно b, или а является кратным b.

Рассмотрим несколько примеров:

Очевидно, что у каждого числа есть бесконечное количество кратных ему чисел. Так, числу 7 кратны числа 7, 14, 21, 28 и т.д.Ряд можно продолжать бесконечно, просто умножая 7 на каждое следующее натуральное число:

А вот количество делителей ограничено. Так, число 15 делится только на 1, 3, 5, 15, а также на –1, –3, –5 и –15. Есть одно исключение – ноль делится на любое целое число (кроме нуля), а потому имеет бесконечное число делителей. Стоит уточнить, что часто под делителями натурального числа понимают только другие натуральные числа, то есть отрицательные делители не учитывают.

Теперь рассмотрим некоторые свойства делимости чисел (для удобства будем пронумеровывать правила, чтобы было легче ссылаться на них).

Действительно, при делении целого числа на себя получается единица:

Ноль является исключением, поскольку деление на ноль не допускается в алгебре.

При делении на единицу число не меняется:

поэтому, если а – целое, то после деления на единицу оно останется целым.

Приведем пример. 128 делится на 16:

В свою очередь 16 делится на 4:

Значит, и 128 делится на 4:

Теперь докажем это свойство более строго. Если а делится на b, а b делится нацело на c, то, по определению делимости, должны существовать такие целые m и k, для которых выполняются равенства:

Подставим второе равенство в первое

Так как произведение целых чисел k и m само является целым, то, опять-таки по определению делимости, а делится нас.

Тоже самое доказательство поясним на конкретных числах.

Пусть 210 делится нацело на 30, а 30 делится на 6. Тогда требуется доказать, что 210 делится на 6 (не выполняя самого деления). 210 можно представить в виде

в свою очередь 30 можно записать как

Теперь подставим вторую запись в первую:

150 = 30•7 = (6•5)•7 = 6•(5•7)

Так как числа 5 и 7 целые, то целым является и их произведение, следовательно, 150 делится на 6.

24 2 :12 2 = 576:144 = 4

Докажем строго это свойство. По определению можно записать равенство

Возведем правую и левую часть равенства в степень n:

а n = (сb) n = c n b n

Делимость суммы чисел

Существуют свойства, которые позволяют определить делимость суммы, даже не вычисляя ее.

Например, числа 3, 6, 9, 12, 15, 18 делятся на 3, поэтому и их сумма должна быть кратна 3:

3 + 6 + 9 + 12 + 15 + 18 = 63

Докажем это для случая с тремя слагаемыми. Пусть числа а, b и с делятся на р. Тогда можно записать выражения

Упростим сумму слагаемых, вынеся множитель p за скобки:

а + b + c = tр + sp + wp = p(t + s + w)

Ясно, что сумма целых чисел t + s + w сама является целой. Следовательно, сумма а + b + c делится на р (по определению).

Естественно, что обратное утверждение ошибочно. Из того факта, что сумма чисел делится на число, не следует, что на него делятся и слагаемые. Например, сумма 5 + 11 + 17 делится на 3:

Однако по отдельности 5, 11 и 17 на тройку не делятся.

Доказанный признак делимости суммы можно использовать при решении некоторых задач.

Пример. Докажите, не используя калькулятор, что число 736263 делится на 737.

Решение. Представим число 736263 как сумму:

736263 = 737000 – 737 = 737000 + (– 737)

Очевидно, что оба слагаемых делятся на 737:

Значит, и их сумма, то есть 736263, делится на 737.

В данном случае мы представили 736263 как сумму положительного и отрицательного числа. Однако делать это было необязательно, так как верно следующее правило:

Доказательство этого факта производится абсолютно также, как и доказательство для суммы чисел.

Следующее свойство помогает доказать неделимость чисел:

Пусть даны числа 40, 44, 48, 52 и 53. Все они, кроме числа 53, кратны 4. Значит, их сумма недолжна делиться на 4 (из-за единственного слагаемого 53). Действительно

40 + 44 + 48 + 52 + 53 = 237

Доказать это очень просто. Покажем это на примере 3 слагаемых. Пусть а и b кратны с, а d ему не кратно. Тогда сумму а, b и d можно представить так:

Поделим эту сумму на с:

((a + b) + d) = (а + b):c + d:с

Ясно, что величина (а + b):c будет целым числом. По условию d:c – дробное число, ведь d не делится на с. Однако сумма дробного и целого числа всегда является также дробным числом. Следовательно, сумма а + b + d не делится на с.

Это свойство очень полезно, так как с его помощью доказываются почти все признаки делимости чисел.

Аналогично можно доказать, что если разность двух чисел не делится на c, если одно из этих двух чисел делится, а второе не делится на с. Например, разность

не кратна 17, так как 17000000 делится на 17, а 16 – нет.

Однако нельзя сформулировать каких-либо правил для тех случаев, когда уже два и более слагаемых не делятся на какое-то число. Так сумма 22 + 44 делится на 6, хотя по отдельности ни 22, ни 44 не кратны 6.

Пример. Делится ли на 29 сумму чисел 58, 290, 2900, 20 и 9?

На первый взгляд, здесь есть два слагаемых, не кратных 29 – это 20 и 9, поэтому сразу ответить на вопрос задачи не получится. Преобразуем сумму, сложив отдельно слагаемые, не кратные 29:

58 + 290 + 2900 + 20 + 9 = 58 + 290 + 2900 + (20 + 9) =

Теперь у нас получилась сумма, где все слагаемые кратны 29, значит, и вся сумма делится на 29.

Пример. Кратна ли 31 сумме слагаемых 310, 62, 620, 93, 11, 10 и 12?

Решение. Здесь есть три слагаемых, не кратных 31: 11, 10 и 12. Сделаем из них одно слагаемое, преобразовав выражение:

310 + 62 + 620 + 93 + 11 + 10 + 12 = 310 + 62 + 620 + 93 + (11 + 10 + 12) =

= 310 + 62 + 620 + 93 + 33

Получили сумму, в которой все слагаемые, кроме 33, кратны 31. Значит, вся сумма не делится на 31.

Делимость произведения чисел

Следующее свойство касается уже делимости произведения чисел.

Приведем пример. Число 35 делится на 5, поэтому и произведение 35 и, скажем, 7 также делится на 5:

Докажем этот факт. Пусть даны числа а и b, причем а кратно с. Тогда можно записать, что

где p какое-то целое число. Произведение а и b можно представить так:

Так как произведение целых чисел p и b также является целым, то получили, что произведение а•b кратно с.

Проиллюстрируем это же доказательство на конкретном примере. Пусть есть произведение чисел 30 и 8 (30•8 = 240). Известно, что 30 делится на 6. Докажем, что и произведение 30•8 кратно шести. По определению делимости можно записать, что:

Подставим это равенство в произведение:

Так как произведение 5•8, очевидно, целое, то по определению делимости 30•8 делится нацело на 6.

Покажем это на примере 33 и 36. 33 кратно 11, а 36 делится на 12. Из этого следует, что произведение 33•36 делится на 11•12. Проверим это:

Докажем это свойство делимости произведения. Пусть а делится на с, а b кратно d. Тогда можно записать равенства

где p и k – какие-то целые числа. Тогда произведение аb будет выглядеть так:

Это значит, что ab делится на cd, так как произведение pk является целым числом.

Рассмотрим, как на координатной прямой располагаются кратные числа. Числа, кратные 2, показаны красным цветом:

Каждое следующее кратное получается при добавлении к предыдущему двойки:

Видно, что среди двух соседних чисел одно обязательно делится на 2.

Теперь посмотрим на расположение чисел, кратных 3 (отмечены зеленым цветом):

Здесь работает тот же принцип. Первым кратным является ноль, а каждое следующее кратное получается добавлением к предыдущему тройки:

Также можно увидеть, что среди трех последовательных чисел одно обязательно будет кратно 3.

Наконец, посмотрим на расположение чисел, кратных 4 (синий цвет):

Здесь можно отметить, что среди любых 4 последовательно идущих чисел (например, 11, 12, 13, 14) ровно одно будет делиться на 4.

Обобщая всё это, можно сформулировать такое правило:

Из этого, в свою очередь, следует следующее утверждение:

Действительно, если хоть один множитель произведения кратен n, то и всё произведение будет кратно n. А среди n последовательных множителей найдется тот, который кратен n.

С помощью этого утверждения можно сразу сказать, что, например, произведение 2522•2523•2524 кратно 3.

Теперь рассмотри несколько задач, в которых используются описанные свойства.

Пример. Делится ли выражение 3 11 + 9 6 + 27 3 на 111?

Представим все слагаемые как степени тройки:

3 11 + 9 6 + 27 3 = 3 11 + (3 2 ) 6 + (3 3 ) 3 = 3 11 + 3 2•6 + 3 3•3 =

= 3 11 + 3 12 + 3 9 = 3 9 (3 2 + 3 3 + 1) = 3 9 (9 + 27 + 1) = 3 9 •37

Далее преобразуем выражение, «забрав» одну тройку у 3 9 и «передав» ее 37:

3 9 •37 = 3 8 •3•37 = 3 8 •(3•37) = 3 8 •111

Итак, исходное выражение можно представить как произведение, причем один из множителей будет кратен 111. Значит и всё выражение делится на 111.

Пример. Имеет ли уравнение

66х 5 + 9х 3 + 36х + 40 = 0

целый корень, который НЕ является делителем числа 40?

Решение. Предположим, что такой корень существует, обозначим его как k. Тогда при его подстановке в уравнение получим верное равенство:

66k 5 + 9k 3 + 36k+ 40 = 0

Теперь поделим обе части уравнения на k:

66k 4 + 9k 2 + 36 + 40/k = 0

Кстати, для приведенного выше уравнения можно доказать, что у него и вовсе отсутствуют целые корни. Попробуйте это сделать самостоятельно.

Прежде, чем рассмотреть следующую задачу, напомним уже известные нам три факта о сумме четных и нечетных чисел:

Пример. Докажите, что разность квадратов двух нечетных чисел делится на 8.

Решение. Известно, что любое нечетное число можно представить в виде

где n – какое-то целое число:

Обозначим первое нечетное число как 2m + 1, а второе как 2р + 1, тогда разность их квадратов, используя формулу сокращенного умножения, можно записать так:

(2m + 1) 2 – (2р + 1) 2 = (2m + 1 + 2р + 1)(2m + 1 – (2р + 1)) =

= (2m + 2p + 2)(2m – 2p) = 2(m + p + 1)•2(m – p) =

Далее следует рассмотреть два случая:

1) Предположим, что m и p являются одновременно либо четными, либо нечетными. Математики говорят в таком случае, что числа m и p имеют одинаковую четность. Тогда разность (m – p) также будет четной, то есть она делится на 2. Получаем, что в произведении

первый множитель делится на 4, а третий – на 2. Тогда и всё произведение, по правилу 8, делится на 4•2 = 8.

2) Теперь предположим, что одно из чисел m и p является нечетным, а другое четным. То есть они имеют разную четность. Тогда сумма (m + p) будет нечетной, а сумма (m + p + 1), наоборот, четной. Получается, что в произведении

первый множитель делится на 4, а второй – на 2. И тогда, снова по правилу 8, всё это произведение должно делиться на 4•2 = 8.

Пример. Есть ли на графике уравнения

2х + 6у = 11

хотя бы одна точка, имеющая целочисленные координаты?

Поделим исходное уравнение на 2:

Предположим, что существует точка с целыми координатами х и у, лежащая на графике этого уравнения. Если подставим ее координаты в уравнение, то в левой части получим, очевидно, какое-то целое число. В правой же части стоит дробное число 5,5. Получается противоречие, значит, точки с целочисленными координатами не существует.

Ответ: такой точки нет.

Деление с остатком

Сейчас мы знаем, что при делении чисел может получиться дробный ответ:

Однако в младшей школе, когда дробные числа ещё не были изучены, использовалось деление с остатком:

Остаток должен быть меньше, чем делитель. Если вычесть из делимого остаток, то получится число, кратное делителю:

Если же остаток получился равным нулю, то имеет место деление без остатка.

Сформулируем строгое определение для операции «деление с остатком»:

Число 75 можно представить как

поэтому результатом деления 75 на 10 будет

Условие 0 ⩽d 2 = 16n 2 = 4•4n 2 + 0 (остаток от деления на 4 равен 0)

(4n + 1) 2 = 16n 2 + 8n + 1 = 4(4n + 2n) + 1 (остаток равен 1)

(4n + 2) 2 = 16n 2 + 16n + 4 = 4(4n 2 + 4n + 1) + 0 (остаток 0)

(4n + 3) 2 = 16n 2 + 24n + 9 = 4(4n 2 + 6n + 2) + 1 (остаток 1)

Получается, что при делении квадрата любого числа на 4 получается либо остаток, равный 1, либо нулевой остаток (то есть имеет место деление нацело).

Принцип Дирихле

Иногда при решении задач, связанных с делимостью чисел, помогает использование принципа Дирихле. Звучит он так:

Формулировка довольно сложная, поэтому для простоты часто используют пример с голубями и клетками:

Посмотрите на рисунок, где изображены 10 голубей и 9 клеток:

Действительно, здесь не получится распределить птиц по клеткам так, чтобы в каждом была не более чем одна птица. Однако на этом принцип Дирихле не исчерпывается. Что можно сказать о случае, когда животных меньше, чем клеток? Ясно, что одна из них останется пустой.

На рисунке показан случай, когда есть 7 голубей и 9 клеток:

Пусть есть поле, разбитое на 4 квадрата. На нем размещено 9 кругов:

Ясно, что в одной из клеток будет более 1 кружочка. Но более того, в одном из них обязательно окажется более 2 кругов! Действительно, даже если в каждом квадрате находилось бы ровно 2 фигуры, то тогда их общее количество равнялось бы 4•2 = 8, а их 9. Но также ясно, что хотя бы в одном квадрате будет менее 3 кругов.

Здесь мы приходим к связи между принципом Дирихле и делением с остатком. Если поделить 9 на 4, то получим 2 и в остатке 1:

2 – это неполное частное. Получается, что отношение 9/4 находится как бы между числами 2 и 3:

60 = 2•30 = 2•2•15 = 2 2 •15

144 = 2•72 = 2•2•36 = 2•2•2•18 = 2•2•2•2•9 = 2 4 •9

64 = 2•32 = 2•2•16 = 2•2•2•8 = 2•2•2•2•4 = 2•2•2•2•2•2 = 2 6 •1

Если же число нечетное, то его можно записать как произведение нечетного числа и двойки в нулевой степени:

Получается, что любое натуральное число z можно представить в виде

где n – неотрицательное целое число, а k – нечетное число, которое, очевидно, не больше самого z.

Представим в таком виде все числа от 1 до 10000. При этом в качестве нечетного числа k мы сможем использовать только те 5000 нечетных чисел, которые не больше 10000. Теперь выберем 5001 число. В силу принципа Дирихле ясно, что хотя бы у двух из них число k будет совпадать. Но если у двух чисел это число k совпадает, то одно из них обязательно делится на другое!

Действительно, пусть одно число представимо как 2 n •k,а второе как 2 m •k, причем n>m. Тогда получаем

то есть при делении 2 n •k на 2 m •k получается целое число – какая-то степень двойки. Например, число 144 представимо как

поэтому 144 делится на 36:

Так как число k может принимать только 5000 значений (именно столько нечетных чисел находится между 1 и 10000), а нам надо сформировать множество из 5001 числа, то по принципу Дирихле мы в любом случае выберем два числа с одинаковым k. Одно из них будет делиться нацело на другое, поэтому сформировать требуемое множество не удастся.

Признаки делимости

На практике очень часто требуется быстро оценить, делится ли число на какое-либо другое число, не выполняя при этом саму операцию деления. Для ряда чисел существуют признаки делимости, которые позволяют произвести такую оценку.

Простейшим является признак делимости на 2:

Например, на 2 делятся числа:

Не кратны двойке числа, заканчивающиеся нечетной цифрой:

Теперь докажем признак делимости чисел на 2. Любое десятичное число можно представить как сумму нескольких десятков и единиц, например:

123456789 = 12345678•10 + 9

В общем случае эта запись будет выглядеть так:

где a – какое-то целое число

Ясно, что слагаемое 10а делится на 2, так как один из множителей этого произведения (10) кратен 2. Поэтому если b четное, то все слагаемые в сумме делятся на 2, следовательно, вся сумма кратна 2. Если же b – нечетная цифра, то получаем сумму, в которой ровно одно слагаемое не делится на 2, а значит, и вся сумма не кратна 2.

Далее рассмотрим признак делимости на 5:

Это значит, что на 5 делятся лишь числа, оканчивающиеся нулем или пятеркой, например:

Доказательство этого признака почти совпадает с предыдущим. Любое число можно переписать как сумму

первое слагаемое 10а делится на 5. Если и b (а это и есть последняя цифра) будет делиться на 5, то, по правилу 4, и вся сумма кратна пяти. Если же b не делится нацело на 5, то в силу правила 6 сумма на пять не делится.

Далее узнаем, как быстро определить, делится ли число на 4:

Приведем следующие примеры чисел, делящихся нацело на 4:

Доказательство этого признака построено на том, что целые числа можно переписать как сумму нескольких сотен и единиц:

123456789 = 1234567•100 + 89

В общем случае эта запись выглядит так:

где b – это число из двух последних цифр. И снова можно утверждать, что слагаемое 100а кратна 4, а значит, именно отделимости b на 4 зависит, будет ли и вся сумма кратна 4.

Так как 100 кратно ещё и 25, то абсолютно аналогично доказывается следующее утверждение:

То есть 25 кратны только те числа, которые оканчиваются на 00, 25, 50 или 75:

Доказательство аналогично доказательству для делимости на четверку.

Далее мы узнаем, какие числа кратны 8:

Так, будут кратны 8 следующие числа:

Если же последние три цифры не кратны 8, то и всё число не кратно восьмерке:

Для доказательства утверждения будем записывать числа как сумму тысяч и единиц:

1356845 = 1356•1000 + 845

В общем случае такое представление будет выглядеть так:

где b состоит из трех последних цифр числа. Слагаемое 1000а делится на 8 при любом значении а, поэтому делимость всей суммы 1000а + b на 8 зависит исключительно от того, кратно ли b восьми.

Еще раз проясним момент, почему иногда мы смотрим только на одну последнюю цифру, а иногда на 2 или даже 3 цифры. Любые целые числа можно при необходимости разложить на сумму десятков, сотен или тысяч и единиц:

6563 = 656•10 + 3 (это разложение используется для проверки делимости на 2)

6563 = 65•100 + 63 (используется для проверки делимости на 4)

6563 = 6•1000 + 563 (используется для проверки делимости на 8)

Слагаемое, содержащее 10, делится на 2, поэтому для проверки делимости на эти числа достаточно проверить одну последнюю цифру. Однако 10 не делится на 4, поэтому для четверки такой способ НЕ подходит. Зато на 4 делится 100, поэтому можно проверить две последние цифры. Наконец, 100 не делится нацело на 8, зато на восьмерку делится 1000, поэтому здесь проверяют три последние цифры

К сожалению, для числа 3 похожий метод (проверка последних цифр) НЕ подходит. Вместо этого необходимо проверять сумму всех цифр:

Так, кратны трем будут числа:

Не кратны трем будут числа, у которых цифры в сумме не делятся нацело на 3:

Теперь докажем признак делимости на 3. Все числа можно представлять как сумму различных степеней двойки

256 = 2•100 + 5•10 + 6•1 = 2•10 2 + 5•10 1 + 6•10 0

4567 = 4•10 3 + 5•10 2 + 6•10 1 + 7•10 0

Собственно, на этом и основана десятичная система счисления. Рассмотрим для примера шестизначное число, которое состоит из цифр abcdef. Его можно представить так:

abcdef = a•10 5 + b•10 4 + c•10 3 + d•10 2 + e•10 1 + f =

= a•100000 + b•10000 + c•1000 + d•100 + e•10 + f =

=99999a + a + 9999b + b + 999c + c + 99d + d + 9e + e + f =

= (99999a + 9999b + 999c + 99d + 9e) + (a + b + c + d + e + f)

Получили сумму двух слагаемых. Первое из них,

(99999a + 9999b + 999c + 99d + 9e)

очевидно, делится на 3, так как числа, состоящие из одних 9, кратны 3:

Второе же слагаемое,

как раз и представляет собой сумму цифр исходного числа. Именно от его кратности тройке зависит, будет ли всё число делиться на 3.

Так как числа, состоящие исключительно из девяток, делятся не только на 3, но и на 9, то абсолютно аналогично доказывается признак делимости на 9:

Так, кратны 9 числа:

Отметим, что существует ещё много признаков делимости для таких чисел, как 7, 11, 13, 17 и т. д, но они достаточно сложные и не очень нужны на практике. Однако есть одно важное правило

Например, если число кратно 3 и 5, то оно делится и на 3•5 = 15, например:

Этот факт следует из того, что любое составное число раскладывается на простые множители. Например, разложение числа 105 выглядит так:

Естественно, что среди простых множителей окажутся именно те числа, на которые делится разлагаемое число. Вспомним уже изученное правило, что если в произведении есть множители, кратные m и n, то всё произведение кратно и mn. Из этого следует, что число делится на произведение простых чисел исключительно в том случае, когда оно кратно каждому из этих простых чисел.

Это свойство помогает сформулировать ещё несколько правил делимости:

Рассмотрим отдельно деление на десять. Число кратно двум, если оно оканчивается цифрами 0, 2, 4, 6 или 8. На 5 же оно делится, если в конце стоит 0 или 5. Получается, что число может одновременно делиться и на 2, и на 5 исключительно в том случае, если его последняя цифра – ноль.

Ещё раз уточним, что каждый из приведенных признаков делимости может использоваться только для своего числа. Ни в коем случае нельзя, например, при проверке делимости 9 использовать признаки делимости на 2 или 10.

Источник