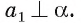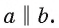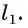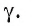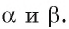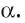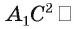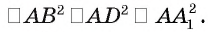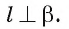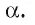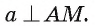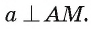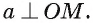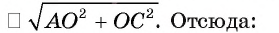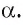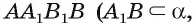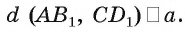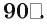доказательство что прямая перпендикулярна плоскости
Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости
Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.
Перпендикулярные прямая и плоскость – основные сведения
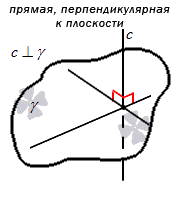
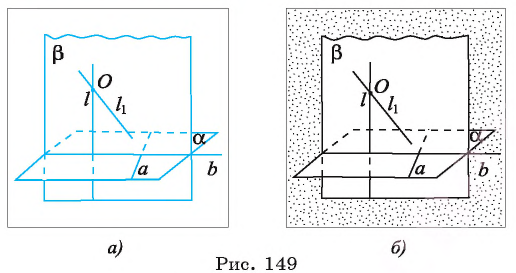
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.
Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.
Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.
При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.
Перпендикулярность прямой и плоскости – признак и условия перпендикулярности
Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.
Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.
При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.
Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.
Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.
Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.
Необходимо произвести проверку выполнимости условия. Получаем, что
Ответ: прямая и плоскость перпендикулярны.
Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.
Ответ: прямая и плоскость не перпендикулярны.
Содержание:
Перпендикулярность прямой и плоскости:
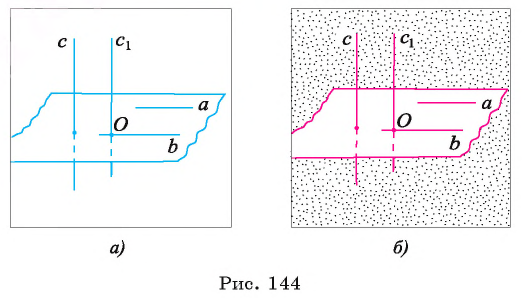
Определение. Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.
Если прямая а перпендикулярна плоскости
Представление о части прямой, перпендикулярной плоскости, дает прямая пересечения поверхностей стен комнаты по отношению к плоскости пола. Колонны здания расположены перпендикулярно по отношению к плоскости фундамента.
В дальнейшем понадобится следующая теорема о перпендикулярности двух параллельных прямых третьей прямой.
Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
Пусть а и b — параллельные прямые и 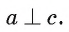
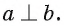
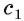
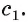
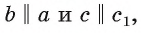
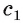
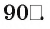
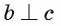
Теперь докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью плоскости.
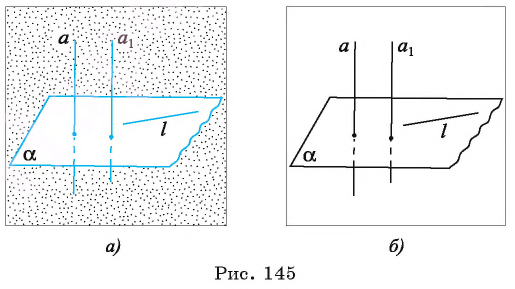
Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Пусть прямые а и 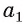
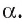
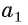
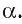
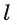
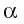
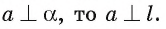
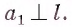
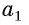
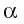
Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
Пусть прямые а и b перпендикулярны плоскости 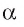
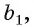
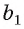
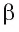
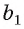
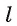
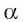
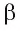
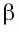
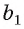
Для установления факта перпендикулярности прямой и плоскости достаточно проверить перпендикулярность прямой только двум пересекающимся прямым, лежащим в этой плоскости. Это вытекает из следующей теоремы.
Признак перпендикулярности прямой и плоскости
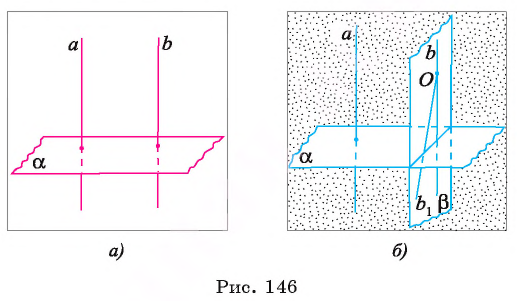
Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Пусть прямая а перпендикулярна прямым р и q, лежащим в плоскости 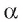
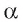
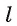
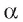
Рассмотрим первый случай, когда прямая а проходит через точку О. Проведем через точку О прямую 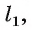
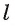
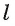
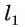
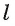
Заметим, что 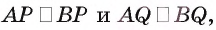



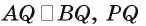
Треугольники APL и BPL равны (так как 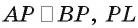


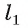
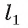
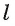
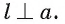
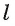
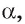
Если прямая а не проходит через точку О, тогда проведем через точку О прямую 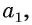
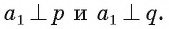
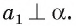
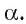
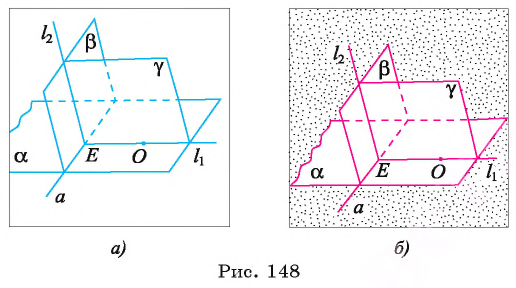
Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
I. Докажем существование плоскости.
Пусть а — данная прямая, а точка О — произвольная точка пространства. Докажем, что существует плоскость, проходящая через точку О и перпендикулярная прямой а.
1)Рассмотрим плоскость 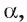
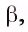
2)В плоскости а через точку О проведем прямую 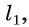
3)Через точку Е в плоскости 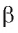
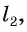
4)Плоскость 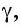
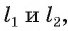
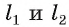
II. Докажем единственность плоскости.
Допустим, что через точку О проходит еще одна плоскость 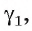
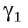
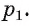
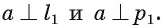
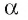
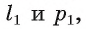
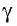
Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
I.Докажем существование прямой.
Пусть дана плоскость а и точка О — произвольная точка пространства. Докажем, что существует прямая, проходящая через точку О и перпендикулярная плоскости 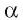
1)Проведем в плоскости 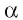
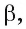
2)Обозначим буквой b прямую, по которой пересекаются плоскости
3)В плоскости 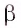
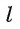
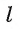
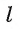
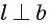
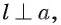
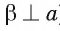
II.Докажем единственность плоскости.
Предположим, что через точку О проходит еще одна прямая 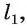
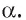
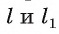
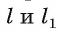
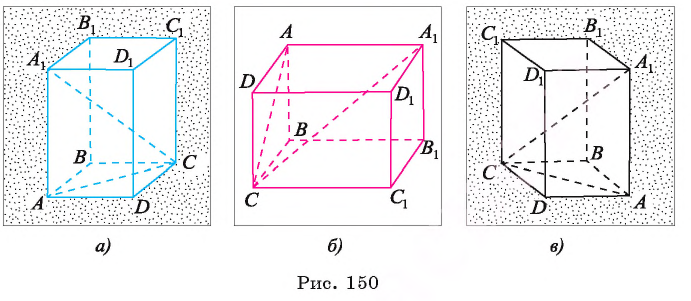
Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину.
Пусть 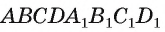
Из условия следует, что 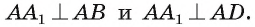
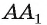
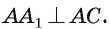
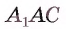
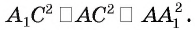
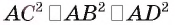
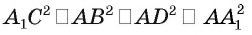
Следствие. Диагонали прямоугольного параллелепипеда равны.
Пример:
Докажите, что если прямая перпендикулярна одной из двух параллельных плоскостей, то эта прямая перпендикулярна и другой плоскости.
Пусть плоскости 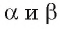
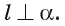
Перпендикуляр и наклонная
Пусть точка А не лежит на плоскости 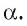
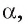
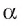
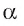
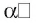
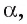
Например, если 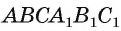
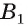
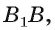
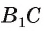
Теорема о трех перпендикулярах
Докажем теорему, которая играет важную роль при решении многих задач.
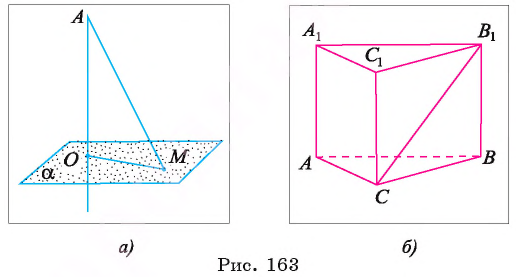
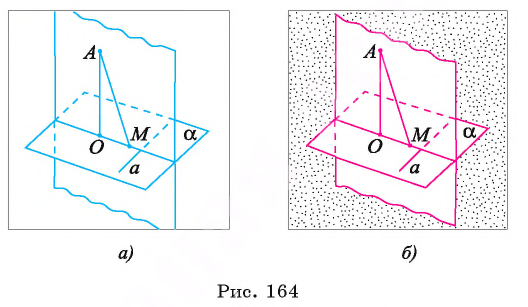
Теорема 1 (о трех перпендикулярах). Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной.
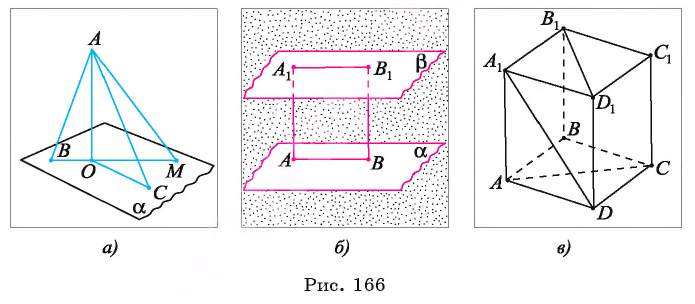
Пусть АО и AM — соответственно перпендикуляр и наклонная к плоскости 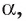
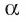
Прямая а перпендикулярна плоскости ОАМ, так как она перпендикулярна двум пересекающимся прямым OA и ОМ этой плоскости ( 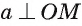
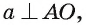
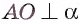
Теорема 2. Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость.
Пусть АО и AM — соответственно перпендикуляр и наклонная, проведенные из точки А к плоскости 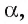
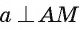
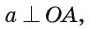
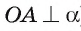
Пример №1
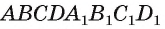
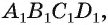
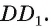
1) 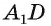
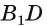
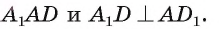
2) 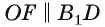
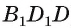
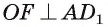
Теорема 3. Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:
1)две наклонные, имеющие равные проекции, равны;
2)из двух наклонных больше та, проекция которой больше.
Пусть АО — перпендикуляр к плоскости 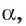
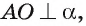
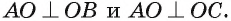
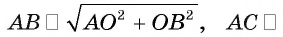
Значит, из всех расстояний от точки А до различных точек плоскости 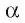
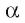
Определение. Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
Расстояние от точки А до прямой 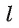
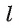
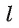
Пусть 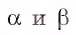
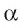
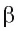
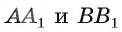
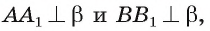
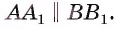
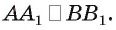
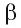
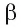
Определение. Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
Расстояние между параллельными плоскостями 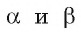
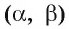
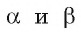
Аналогично, каждая точка прямой, параллельной некоторой плоскости, находится на одном и том же расстоянии от этой плоскости.
Определение. Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
Расстояние между прямой 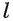
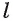
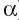
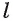
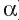
Если две прямые скрещивающиеся, то через каждую из них проходит единственная плоскость, параллельная другой.
Определение. Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.
Расстояние между скрещивающимися прямыми а и b обозначается d (а, b) (читают: « Расстояние между прямыми а и b »).
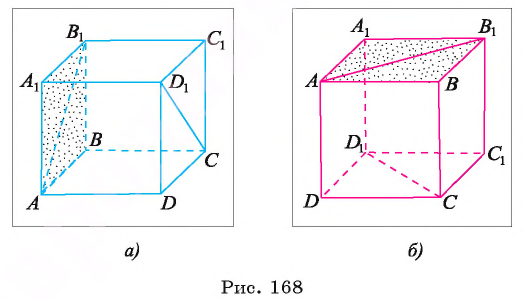
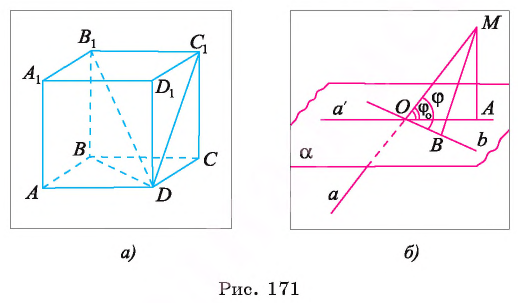
Например, в прямоугольном параллелепипеде 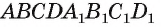
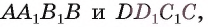
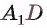
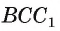
Пример №2
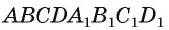
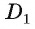
Решение:
1)Заметим, что 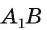
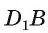
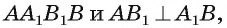
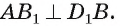
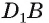
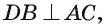
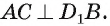
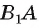
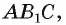
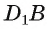
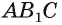
2)Так как 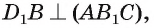
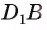
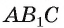
3)Строим точку 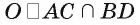
4)Точка 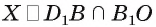
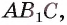
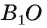
Пример №3
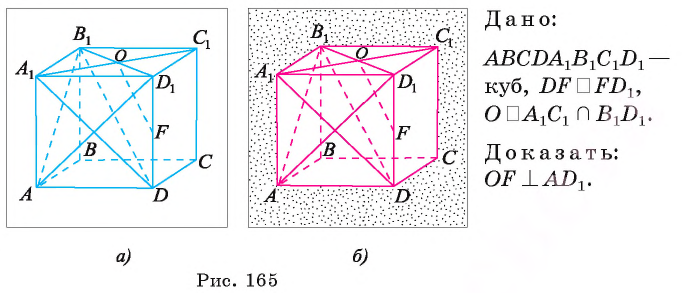
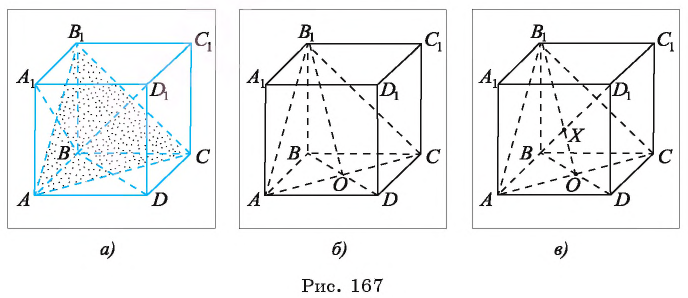
Дан куб 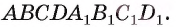
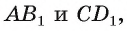
Решение:
1)Рассмотрим плоскость, проходящую через прямую 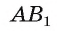
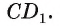
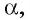
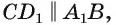
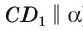
2)Расстояние между прямыми 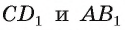
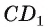
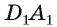
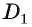

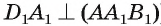
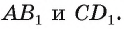
Угол между прямой и плоскостью
Ортогональная проекция прямой
Пусть в пространстве даны плоскость 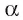
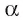
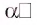
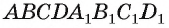
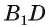
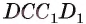
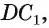
Дадим определение угла между прямой и плоскостью, при этом воспользуемся понятием ортогональной проекции прямой на плоскость.
Если прямая перпендикулярна плоскости, то ее ортогональная проекция на эту плоскость есть точка пересечения этой прямой с плоскостью. В этом случае угол между прямой и плоскостью считается равным
Угол между прямой и плоскостью
Рассмотрим понятие угла между прямой и плоскостью.
Определение. Углом между прямой, не перпендикулярной плоскости, и плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость.
Теорема. Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.
Пусть прямая а пересекает плоскость 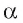
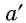
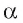
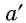
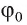
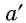
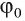
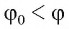
Если прямые а и b не перпендикулярны, то из точки 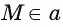

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.