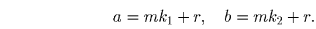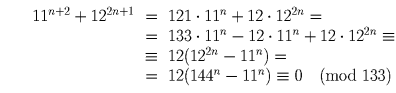докажите что 2343 4323 делится на 66
Докажите что 2343 4323 делится на 66
Задача 1:
Докажите, что a ≡ b (mod m) тогда и только тогда, когда a – b делится на m.
Решение:
Пусть a ≡ b (mod m). Обозначим одинаковый для a и b остаток при делении на m через r. Тогда
Отсюда a – b = m(k 1 – k 2 ) делится на m.
Задача 2:
Если a ≡ b (mod m) и c ≡ d (mod %)%m, то a + c ≡ b + d (mod %)%m.
Решение:
Так как a – b делится на m и c – d делится на m, то (a – b) + (c – d) = (a + c) – (b + d) делится на m, что и требовалось доказать.
Задача 3:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то a – c ≡ b – d (mod %)%m.
Задача 4:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то ac ≡ bd (mod %)%m.
Решение:
ac – bd = ac – bc + bc – bd = (a – b)c + b(c – d) делится на m, что и требовалось доказать.
Задача 5:
Если a ≡ b (mod %)%m, n – натуральное число, то a n ≡ b n (mod %)%m.
Задача 6:
Докажите, что n² + 1 не делится на 3 ни при каком целом n.
Решение:
Ясно, что каждое целое число n сравнимо по модулю 3 либо с 0, либо с 1, либо с 2.
Если n ≡ 0 (mod %)%3, то n² ≡ 0 (mod 3) – (умножение сравнений) и n² + 1 ≡ 1 (mod %)%3 – (сложение сравнений).
Если n ≡ 1 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Если n ≡ 2 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Таким образом, ни в одном случае мы не получим n² + 1 ≡ 0 (mod %)%3.
Задача 7:
Найдите остаток от деления 6¹ºº на 7.
Решение:
Заметим, что 6 ≡ – 1 (mod %)%7. Возводя это сравнение в сотую степень, получаем 6¹ºº ≡ ( – 1)¹ºº (mod %)%7, то есть 6¹ºº ≡ 1 (mod %)%7.
Задача 8:
Докажите, что 30 99 + 61¹ºº делится на 31.
Решение:
30 99 ≡ ( – 1) 99 ≡ – 1 (mod 31) 61¹ºº ≡ ( – 1)¹ºº ≡ 1 (mod 31).
Задача 9:
а) 43¹º¹ + 23¹º¹ делится на 66.
б) a n + b n делится на a + b, если n – нечетное число.
Решение:
б) a n + b n = (a + b)(a n – 1 – a n – 2 b + … + ( – 1) n – 1 b n – 1 )
Задача 10:
Докажите, что 1 n + 2 n + … + (n – 1) n делится на n при нечетном n.
Решение:
Указание: Рассмотрите сумму симметричных слагаемых.
Задача 11:
Докажите, что существует бесконечно много натуральных чисел, не представимых в виде суммы трех точных кубов.
Решение:
Рассмотрите числа вида 8k + 7.
Задача 12:
Докажите, что ни одно из чисел вида 10 3n + 1 нельзя представить в виде суммы двух кубов натуральных чисел.
Решение:
Куб натурального числа сравним по модулю 7 либо с 0, либо с 1, либо с – 1 – проверьте! Поэтому сумма двух кубов сравнима с одним из следующих чисел: – 2, – 1, 0, 1, 2. Заметим, что 10 ≡ 3 (mod %)%7, а 10³ ≡ – 1 (mod %)%7. Поэтому 10 3n + 1 сравнимо либо с 3, либо с – 3 по модулю 7.
Задача 13:
Докажите, что среди 51 целого числа найдутся два, квадраты которых дают одинаковые остатки при делении на 100.
Решение:
Используйте тождество x² – y² = (x – y)(x + y).
Задача 14:
Назовем натуральное число n удобным, если n² + 1 делится на 1000001. Докажите, что среди чисел 1, 2, …, 1000000 четное число удобных.
Решение:
Если x – удобное число, то и 1000001 – x – также удобное.
Задача 15:
а) Может ли квадрат натурального числа оканчиваться на 2?
б) Можно ли, используя только цифры 2, 3, 7, 8 (возможно, по несколько раз), составить квадрат натурального числа?
Решение:
Задача 16:
Какое число нужно добавить к числу (n² – 1)¹ººº (n² + 1)¹ºº¹, чтобы результат делился на n?
Решение:
Например, – 1 или n – 1.
Задача 17:
Найдите остаток от деления на 7 числа 10¹º + 10¹ºº + 10¹ººº + … + 10¹ºººººººººº.
Решение:
Задача 18:
Сколько существует натуральных чисел n, меньших 10000, для которых 2 n – n² делится на 7?
Решение:
Задача 19:
Обозначим через k произведение нескольких (больше одного) первых простых чисел. Докажите, что число а) k – 1; б) k + 1 не является точным квадратом.
Решение:
а) k – 1 = 3p + 2, а по модулю 3 квадраты могут давать лишь остатки 0 или 1.
б) k + 1 = 4q + 3, а по модулю 4 квадраты могут давать лишь остатки 0 или 1.
Задача 20:
Существует ли такое натуральное n, что n² + n + 1 делится на 1955?
Решение:
Нет. n² + n + 1 не может даже делиться на 5.
Задача 21:
Докажите, что 11 n + 2 + 12 2n + 1 делится на 133 при любом натуральном n.
Решение:
Задача 22:
Пусть n – натуральное число такое, что n + 1 делится на 24. Докажите, что сумма всех натуральных делителей n делится на 24.
Решение:
Докажите, что сумма делителей делится и на 3, и на 8.
Задача 23:
а) a 1 = a 2 = 1. Докажите, что ни один из членов последовательности не делится на 4.
б) Докажите, что a n – 22 – составное число при любом n > 10.
Решение:
Докажите что 2343 4323 делится на 66
Задача 1: Разделите с остатком а) – 15 на 7; б) – 224 на 9.
Задача 2: Пусть x = 100k – 16, k – целое. Чему равны частное и остаток при делении x на а) 100; б) 5?
Задача 3: Делимое и делитель увеличили в три раза. Как изменятся неполное частное и остаток?
Задача 4: Докажите, что остаток от деления простого числа на 30 – простое число или единица.
Задача 5: Найдите остаток от деления
1999 2000 2001 + 2001³ на 7;
Задача 6: Найдите остаток от деления 9¹ºº на 8.
Задача 7: Найдите остаток от деления 12¹ºº на 13.
Задача 8: Найдите остаток от деления 2 7 + 2 8 + 2 9 + 2¹º на 5.
Задача 9: Найдите остаток при делении на 7 числа 100¹ºº – 30¹ºº.
Задача 10: Найдите две последние цифры числа 1999²ººº;
Задача 11: Докажите, что
а) произведение 4 последовательных целых чисел;
б) разность квадратов двух простых чисел, больших 3,
Задача 12: Докажите, что если a + 1 делится на 3, то 4 + 7a делится на 3.
Задача 13: Пусть n и m – натуральные числа, причем m ≠ 1. Известно, что 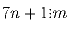
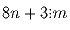
Задача 14: Докажите, что из любых n целых чисел можно выбрать одно или несколько с суммой, кратной n.
Задача 15: Найдите остаток от деления 5 7 – 7 5 на 3.
Задача 16: Докажите, что 23 43 + 43²³ делится на 66.
Задача 17: Найдите последнюю цифру числа 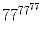
Задача 18: Найдите две последние цифры числа 16²ººº.
Задача 19: Докажите, что если a + 2 делится на 11 и 35 – b делится на 11, то a + b делится на 11.
Задача 20: Назовем автобусный билет с шестизначным номером счастливым, если сумма цифр его номера делится на 7. Могут ли два билета подряд быть счастливыми?
Задача 21: Шайка разбойников отобрала у купца мешок с монетами. Каждая монета стоит целое число грошей. Оказалось, что какую монету не отложи, оставшиеся монеты можно поделить между разбойниками так, что каждый получит одинаковую сумму. Докажите, что число монет без одной делится на число разбойников в шайке.
Докажите что 2343 4323 делится на 66
Докажите, что
а) 2 41 + 1 делится на 83;
б) 2 70 + 3 70 делится на 13;
в) 2 60 – 1 делится на 20801.
Решение
а) 2 9 = 512 ≡ 14 (mod 83), 2 18 ≡ 196 ≡ 30, 2 36 ≡ 900 ≡ 70 ≡ –13, 2 41 ≡ –13·32 ≡ –416 ≡ –1.
б) 2 70 + 3 70 = 4 35 + 9 35 делится на 4 + 9 = 13.
в) 20801 = 11·31·61.
Первый способ. 2 60 – 1 делится на 2 10 – 1 = (2 5 – 1)(2 5 + 1) = 31·33. Это число делится на 31 и на 11. Кроме того, 2 6 ≡ 3 (mod 61), 2 30 ≡ 243 ≡ –1,
2 60 ≡ 1.
Второй способ. Согласно малой теореме Ферма (см. задачу 60736) 2 60 – 1 делится на 61, 2 30 – 1 делится на 31, 2 10 – 1 делится на 11. Поэтому
2 60 – 1 делится на все эти числа.
Замечания
В п. а) школьники, знакомые с квадратичными вычетами могут рассуждать так: (2 41 – 1)(2 41 + 1) = 2 82 – 1 делится на 83 по малой теореме Ферма. Двойка не является квадратичным вычетом по модулю 83, поэтому 2 41 – 1 на 83 не делится. Значит, на 83 делится 2 41 + 1.
Источники и прецеденты использования
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 4 |
| Название | Арифметика остатков |
| Тема | Деление с остатком. Арифметика остатков |
| параграф | |
| Номер | 2 |
| Название | Делимость |
| Тема | Теория чисел. Делимость (прочее) |
| задача | |
| Номер | 04.027 |