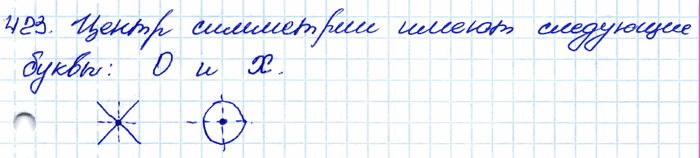докажите что биссектриса угла является его осью симметрии
Геометрия 8 класс Атанасян Задачи 399-423
Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
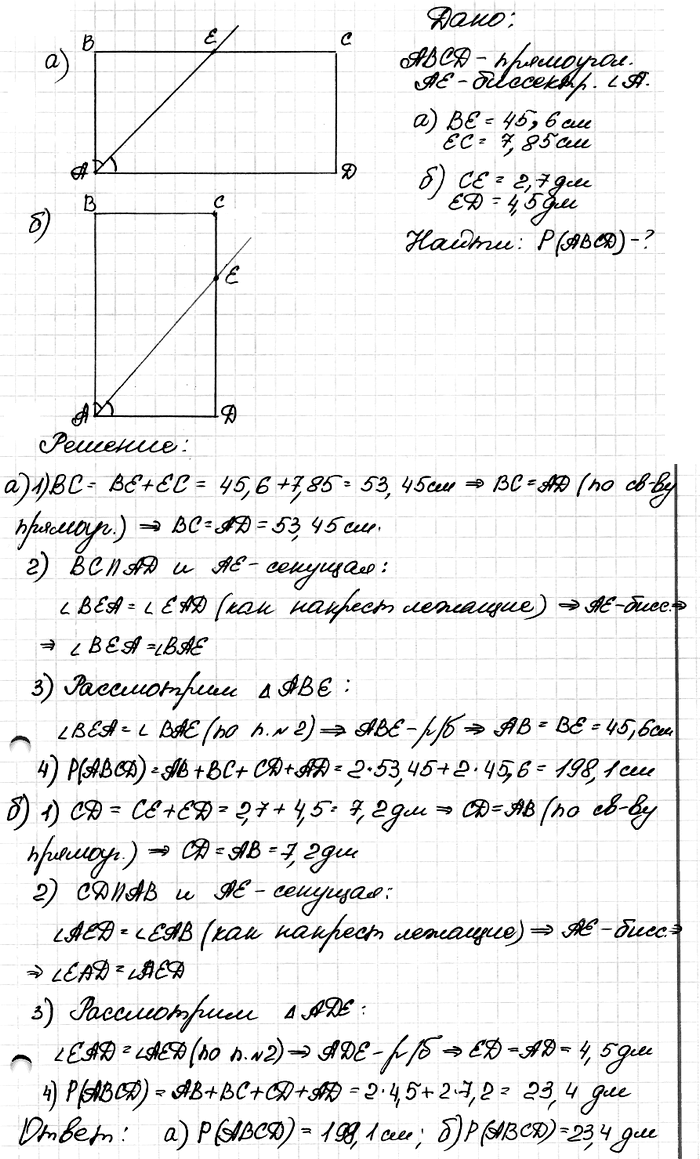
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
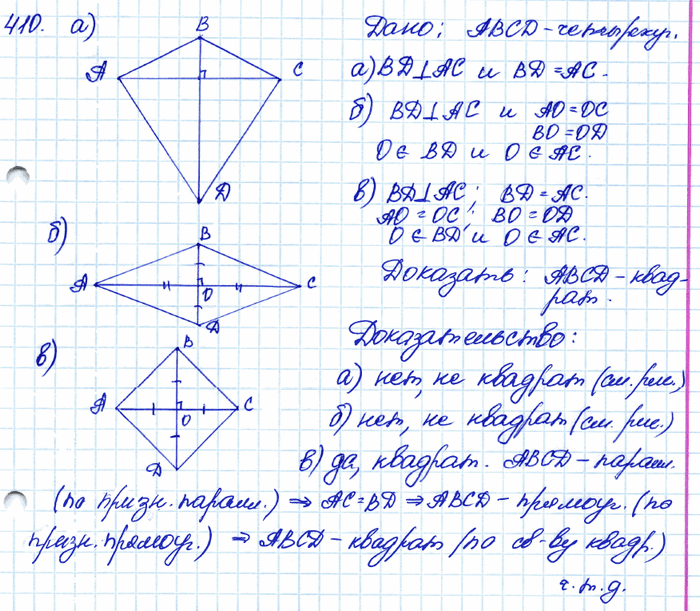
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.