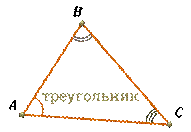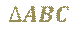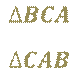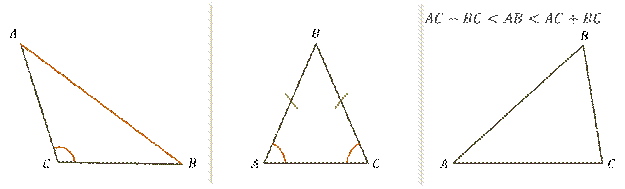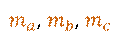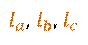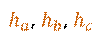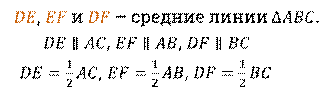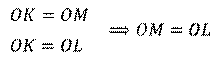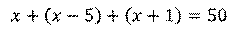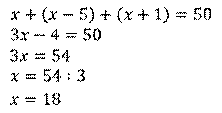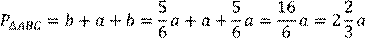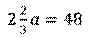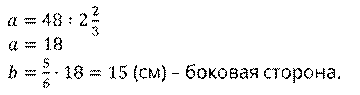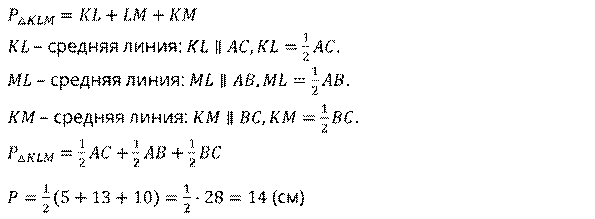докажите что медианы треугольника пересекаются в одной точке
Треугольник. Элементы треугольника
Урок 52. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Треугольник. Элементы треугольника»
· назвать элементы треугольника;
· доказать, что медианы треугольника пересекаются в одной точке;
· доказать, что биссектрисы треугольника также пересекаются в одной точке;
· доказать, что высоты или прямые, содержащие высоты, пересекаются в одной точке.
Треугольник – это одна из самых замечательных и самых важных фигур в геометрии.
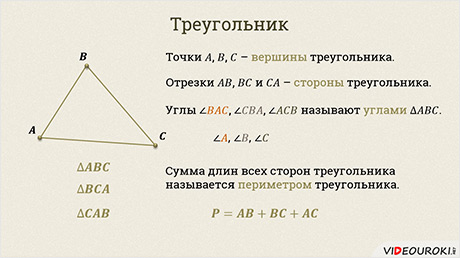
Итак, давайте отметим три точки А, В и С, которые не лежат на одной прямой, и соединим их отрезками. В результате получим геометрическую фигуру, которая и называется треугольником.
Точки 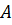
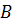
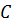
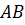
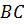
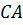
Треугольник, который мы с вами построили, обозначают так:
И говорят «треугольник А Б Ц».
Поменяв буквы местами, этот же треугольник можно обозначить и таким образом:
Углы 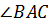
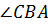
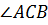

Кстати, углы треугольника можно обозначать и одной латинской буквой: например, ∠𝐴, ∠𝐵, ∠𝐶.
Сумма длин всех сторон треугольника называется периметром треугольника. Т.е. периметр нашего треугольника равен 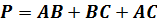
Различают следующие виды треугольников:
— в зависимости от величины углов:
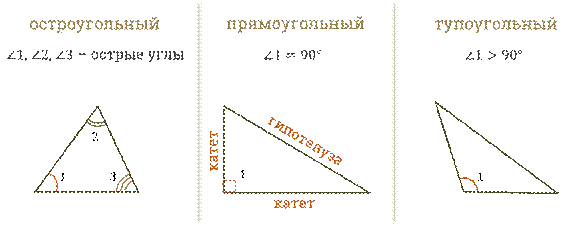
остроугольный (все углы треугольника острые, т.е. меньше 90 о );
прямоугольный (один из углов треугольника прямой, т.е. равен 90 о );
Нужно помнить, что стороны прямоугольного треугольника имеют специальные названия. Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
И третий вид треугольников: тупоугольный (один из углов треугольника тупой, т.е. больше 90 о ).
Затем, треугольники различают в зависимости от величины сторон:
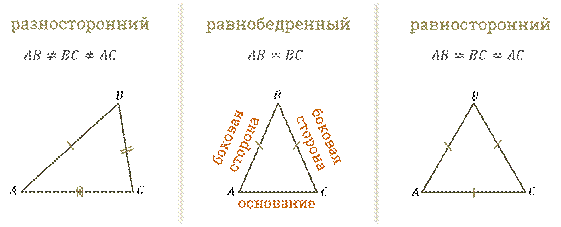
разносторонний (все стороны разной длины);
равнобедренный (две стороны равны и называются боковыми, а третья сторона – основанием);
и равносторонний (все стороны равны между собой).
Во всяком треугольнике против большей стороны лежит больший угол; против равных сторон – равные углы. Любая сторона треугольника меньше суммы и больше разности двух других сторон.
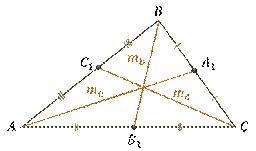
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Любой треугольник имеет три медианы. Например, возьмём треугольник 
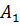
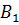
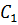
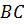
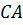
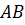
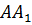
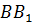
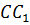
Медианы, проведённые из вершин 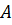
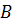
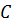

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны.
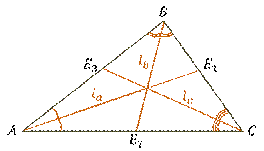
Любой треугольник имеет три биссектрисы. Возьмём некоторый треугольник 
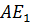
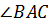
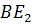
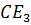
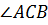
Биссектрисы, проведённые из вершин 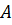
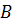
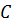

Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону.
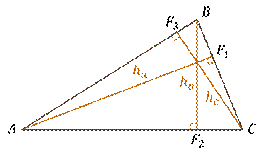
Каждый треугольник имеет три высоты. Изобразим треугольник 
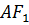
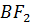
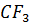
Высоты, проведённые из вершин 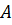
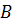
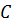

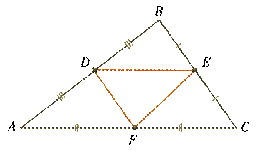
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Поскольку в любом треугольнике три стороны, то треугольник имеет три средние линии. Средняя линия треугольника, соединяющая две данные стороны, параллельна третьей стороне, а её длина равна половине этой стороны.
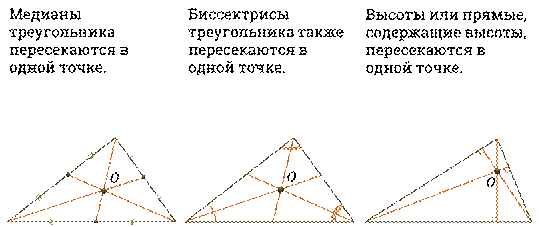
Отметим свойства, которыми обладают медианы, биссектрисы и высоты треугольника.
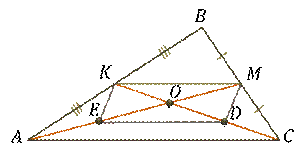
Медианы треугольника пересекаются в одной точке.
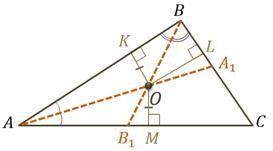
Биссектрисы треугольника также пересекаются в одной точке.
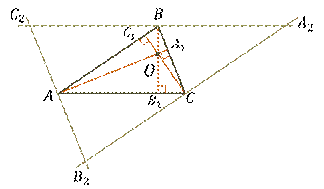
Высоты или прямые, содержащие высоты, пересекаются в одной точке.
Докажем каждое из этих свойств по очереди.
Итак, три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 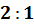
Доказательство. Рассмотрим треугольник 
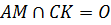
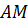
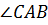
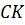
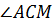
Тогда отрезок 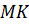

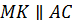
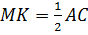
Обозначим середины отрезков 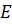
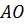
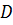
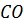
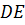
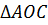
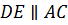
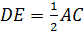
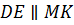
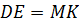
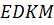
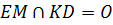
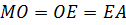
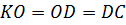
Но тогда 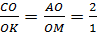
Что и требовалось доказать.
Биссектрисы треугольника пересекаются в одной точке.
Доказательство. Рассмотрим треугольник 
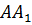
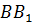
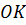
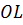
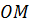
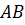
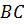
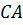
Ранее мы с вами доказали теорему о свойстве точек биссектрисы неразвёрнутого угла. Из этой теоремы следует, что
Т.е. точка О равноудалена от сторон угла 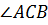
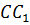

Что и требовалось доказать.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Докажем это утверждение. Рассмотрим произвольный треугольник 
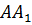
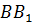
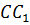
Для этого проведём через каждую вершину треугольника 
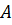
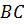
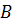
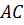
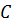
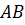
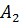
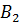
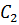
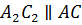
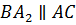
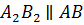
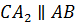
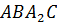
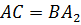
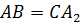
Следовательно, четырёхугольник 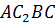
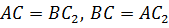
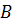
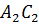
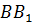
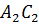
Аналогично точка 𝐴 является серединой отрезка 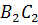
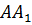
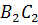
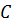
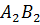
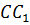
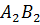
Мы знаем, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Значит, и наши серединные перпендикуляры 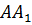
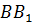
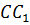
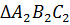


Что и требовалось доказать.
А теперь рассмотрим решения нескольких задач.
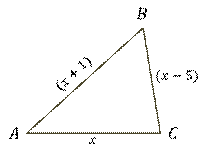
Периметр треугольника равен 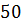
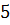
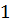
Пусть одна сторона треугольника равна 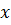
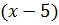
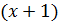
Решим это уравнение. Получим,
Тогда имеем одна сторона треугольника 18 см, вторая 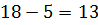
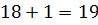
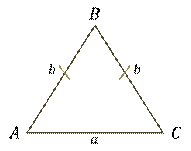
В равнобедренном треугольнике найти неизвестные стороны, если отношение боковой стороны к основанию равно 
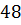
Пусть а – основание, 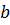
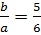
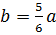
Заменим 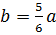
Составим уравнение. Решим его. Тогда получим, что
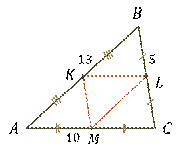
Дан треугольник, стороны которого соответственно равны 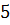
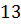
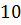
Пусть дан треугольник 
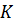
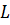
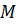
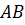
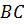
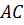
На этом уроке мы говорили о треугольниках. Рассмотрели их элементы. А также доказали, что медианы треугольника пересекаются в одной точке. Биссектрисы треугольника также пересекаются в одной точке. Высоты или прямые, содержащие высоты, пересекаются в одной точке.