докажите что пересечение двух выпуклых фигур выпукло

Докажите что пересечение двух выпуклых фигур выпукло

ВЫПУКЛЫЕ МНОГОГРАННИКИ. ТЕОРЕМА ЭЙЛЕРА

Обычно в школьных курсах геометрии дается следующее определение многогранника.
Определение. Многогранником называется тело, поверхность которого состоит из конечного числа многоугольников.
При этом понятия тела и поверхности, хотя и имеют наглядный смысл, нуждаются в уточнении. Причем их строгие определения используют основные понятия топологии: внутренняя и граничная точка, внутренность и граница, открытость, замкнутость, связность, ограниченность.
Напомним, что окрестностью U _r (A) точки A пространства радиуса r называется фигура, стоящая из всех точек пространства, удаленных от точки A на расстояние, меньшее r. Таким образом,

Точка A пространства называется внутренней точкой фигуры Ф, если у нее существует окрестность, целиком содержащаяся в этой фигуре.
Точка A пространства называется внешней точкой фигуры Ф, если у нее существует окрестность, не содержащая точек фигуры Ф, т.е. целиком лежащая в дополнении к этой фигуре.
Точка A пространства называется граничной точкой фигуры Ф, если она не является ни внутренней, ни граничной точкой этой фигуры, т.е. в любой ее окрестности если как точки фигуры Ф, так и точки, не принадлежащие этой фигуре.
Внутренностью фигуры Ф называется фигура, состоящая из всех внутренних точек этой фигуры.
Фигура Ф называется открытой, если каждая ее точка является внутренней или, что то же самое, фигура Ф совпадает со своей внутренностью.
Границей фигуры Ф называется фигура, состоящая из всех граничных точек этой фигуры.
Фигура Ф называется замкнутой, если все ее граничные точки принадлежат Ф.
Фигура Ф называется ограниченной, если она целиком содержится в некоторой окрестности.
Фигура Ф называется линейно связной, если любые две ее точки можно соединить кривой, целиком содержащейся в этой фигуре.
Фигура Ф называется выпуклой, если любые две ее точки можно соединить отрезком, целиком содержащейся в этой фигуре.
Ясно, что выпуклая фигура является линейно связной. Обратное неверно.
Открытая линейно связная фигура называется областью.
Телом называется ограниченная область вместе со своей границей. Граница тела называется также его поверхностью.
Примерами тел являются куб, параллелепипед, пирамида, шар, цилиндр, конус и др.
Среди общих свойств фигур нам понадобятся следующие.

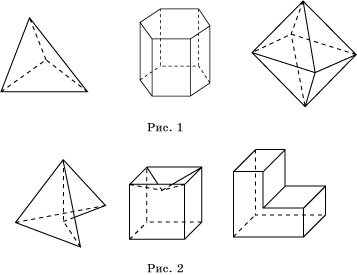
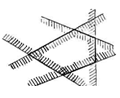
Примеры выпуклых и невыпуклых многогранников приведены на рисунках 1 и 2, соответственно.

Теорема 1. Все грани выпуклого многогранника являются выпуклыми многоугольниками.

Действительно, грань многогранника можно представить как пересечение многогранника и плоскости, содержащей эту грань. После этого остается только воспользоваться свойством 2.

Заметим, что обратное утверждение неверно. А именно, из того, что гранями многогранника являются выпуклые многоугольники, не следует выпуклость самого многогранника. Попробуйте привести примеры таких многогранников.

Поэтому для многогранника справедливо требуемое равенство.
Дадим еще одно доказательство теоремы Эйлера. Рассмотрим какую-нибудь сферу, содержащую данный многогранник, и из внутренней точки многогранника спроектируем его поверхность на эту сферу. Образы ребер многогранника образуют сетку (граф) на сфере. Стянем одно из ребер этой сетки в его вершину. При этом число вершин и ребер уменьшится на единицу, а В – Р + Г не изменится. Будем повторять эту операцию для ребер с двумя вершинами. В результате мы придем к сетке из петель с одной общей вершиной. Будем теперь убирать петли до тех пор, пока не останется одна петля. При этом каждый раз число вершин не меняется, а число ребер и граней уменьшается на единицу. Следовательно В – Р + Г не меняется. Для одной петли на сфере очевидно имеют место равенства В = 1, Р = 1, Г = 2 и, следовательно, имеем равенство В – Р + Г = 2.

Отметим, что равенство Эйлера выполняется не только для выпуклых многогранников, но и для многогранников, поверхность которых гомеоморфна сфере.

На рисунке 3, а, б изображены многогранники, для которых равенство Эйлера не выполняется.

Многогранник на рисунке 3, а получен вырезанием маленького куба внутри большого куба. Для этого многогранника выполняется равенство В – Р + Г = 4. Многогранник на рисунке 3, б получен вырезанием в кубе сквозного прямоугольного отверстия. Для этого многогранника выполняется равенство В – Р + Г = 0.

Задача. Приведите примеры невыпуклых многогранников, поверхности которых гомеоморфны сфере.

Задача. Приведите пример многогранника, поверхность которого не гомеоморфна сфере, но для которого выполняется равенство В – Р + Г = 2.

Рассмотрим несколько следствий теоремы Эйлера о выпуклых многогранниках.

Следствие 2. В любом выпуклом многограннике имеется грань с числом сторон, меньшим шести.

Следствие 3. Для любого выпуклого многогранника имеет место формула

Еще одной важной теоремой о выпуклых многогранниках является теорема Коши, доказанная им в 1813 г. и называемая теоремой о жесткости выпуклого многогранника. Она утверждает, что если два выпуклых многогранника, имеют соответственно равные грани, составленные одинаковым образом, то эти многогранники равны. При этом, слова «составленные одинаковым образом» означают, что если две грани одного многогранника имеют общее ребро, то и соответствующие им грани другого многогранника также имеют общее ребро.

Доказательство этой теоремы можно, например, найти в книгах [2], [3].

Для невыпуклых многогранников указанное в теореме Коши свойство перестает быть верным.

Задача. Приведите примеры двух неравных многогранников, имеющих соответственно равные грани, составленные одинаковым образом.

Источник

Немного о выпуклых фигурах.

Помимо круга, квадрата, треугольников, существует масса других геометрических фигур. Дать всем им название не представляется возможным. Поэтому, как в биологии, где растения и животных разделяют на классы, геометрические фигуры разделяют на классы фигур, похожих между собой. Посмотрим, как это делается в «Словаре русского языка» СИ. Тут наше терпение лопается, поскольку линии могут быть самыми разнообразными. Будет ли треугольник выпуклым? Из приведенных «определений» ничего определенного сказать нельзя.

В математике понятие выпуклой фигуры имеет четко определенный смысл; Теперь ясно, что треугольник — выпуклое тело, а четырехугольники бывают как выпуклые, так и не выпуклые. А какие теоремы можно доказать по данной теме? Таких теорем много. Вот две простейшие.

Общая часть двух выпуклых фигур сама является выпуклой. Доказательство этого утверждения совсем простое: возьмем две точки А и В, принадлежащие как первой, так и второй. Но так как они выпуклые, то отрезок, соединяющий точки А и В, принадлежит и первой и второй, значит, он принадлежит их общей части.

Вторая теорема доказывается более сложно, но факт, содержащийся в ней, гораздо неожиданнее. Требование выпуклости здесь очень важно. Ведь четыре фигуры, из которых только одна выпуклая, таковы, что у любых трех найдется общая точка, и в то же время нет точки, общей всем четырем данным телам.

Если рассмотреть набор данных геометрических тел такой, что каждые две имеют общую точку, то мы не можем гарантировать наличие общей точки для всех их.

Для выпуклых тел в пространстве теорема верна, но с небольшой поправкой: набор выпуклых тел имеет общую точку, если любые четыре тела имеют общую точку.

Эта теорема была сформулирована и доказана в 20-х годах нашего столетия, когда выяснилась важная роль выпуклых тел в приложениях математики к разным областям знаний, особенно к экономике, даже люди, которым интересна погода могут использовать это в своих исследованиях.

Источник

§ Аннотация

Комплект учебно-методических материалов

к учебному модулю: «Моделирование многогранников в компьютерной системе « Maple »» (в рамках дисциплины «Элементарная математика»)

Специальность 032100 “Математика»/ Квалификация «Учитель математики»

Смирнов В.А., заведующий кафедрой элементарной математики, д.ф.-м.н., профессор

конспекта лекций по учебному модулю

Тема : М ногогранники и их свойства.

Основные вопросы, рассматриваемые на лекции:

1. Определение многогранника и его элементов.

2. Внутренние и граничные точки. Внутренность и граница.

3. Открытые и замкнутые фигуры и их свойства.

4. Выпуклые фигуры и их свойства.

5. Тела и поверхности.

Краткое содержание лекционного материала

В учебниках геометрии многогранниками называются тела, поверхности которых состоят из конечного числа многоугольников, назы­ваемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.

При этом понятия тела и его поверхности нуждаются в уточнении. Хотя они имеют наглядный смысл, их строгое определение довольно сложно и использует начальные понятия такого раздела математики, как топология. К ним относятся: внутренняя, внешняя и граничная точки, внутренность, граница, открытость, замкнутость, связность, ограниченность. Рассмотрим эти понятия и их свойства более подробно.

Точка A называется внутренней точкой фигуры Ф, если существует шар с центром в точке A, целиком содержащийся в фигуре Ф.

Точка B называется называется внешней точкой фигуры Ф, если существует шар с центром в точке B, не содержащий точек фигуры Ф.

Точка C называется граничной точкой фигуры Ф, если она не является ни внутренней ни внешней точкой этой фигуры, т.е. в любом шаре с центром в точке C имеются как точки фигуры Ф, так и точки, не принадлежащие фигуре Ф.

Итак, для любой точки по отношению к фигуре Ф есть только три возможности: быть внутренней, внешней или граничной точкой.

Внутренностью фигуры Ф называется фигура, состоящая из всех ее внутренних точек. Будем обозначать ее вн( Ф). Ясно, что фигура вн( Ф) содержится в фигуре Ф.

Фигура Ф называется открытой, если она совпадает со своей внутренностью, т.е. Ф = вн( Ф). Таким образом, у открытой фигуры все точки являются внутренними.

В качестве примера рассмотрим фигуру, состоящую из всех точек, удаленных от данной точки O на расстояние меньшее R. Обозначим ее U( O, R) и докажем, что она является открытой. Для этого нужно доказать, что каждая ее точка является внутренней.

Пусть A – произвольная точка фигуры U( O, R). Обозначим через d расстояние от A до O и рассмотрим шар V с центром в точке A и радиусом r = ( R – d). Если точка X принадлежит этому шару, то расстояние от нее до A меньше или равно r и, следовательно, меньше R – d. В силу неравенства треугольника, расстояние от X до O меньше или равно сумме расстояний от X до A и от A до O, т.е. меньше чем R – d + d = R. Это означает, что точка X принадлежит фигуре U( O, R). Поскольку X – произвольная точка шара V, то V содержится в U( O, R). Следовательно, A – внутренняя точка фигуры U( O, R). Что и требовалось доказать.

Доказательство. Пусть Ф₁ и Ф₂ – открытые фигуры, Ф – их пересечение. Если A принадлежит Ф, то она принадлежит как Ф₁ так и Ф₂. Из открытости этих фигур следует, что существуют шары с центром в этой точке и радиусами R₁ и R₂ соответственно, целиком содержащиеся в этих фигурах. Обозначим через R наименьший из этих радиусов. Тогда шар с центром в точке A и радиусом R будет содержаться как в фигуре Ф₁ так и в фигуре Ф₂. Значит, он будет содержаться в пересечении Ф и, следовательно, точка A является внутренней точкой фигуры Ф. Поскольку A – произвольная точка фигуры Ф, то Ф – открытая фигура.

Границей фигуры Ф называется фигура, состоящая из всех ее граничных точек. Будем обозначать ее гр( Ф).

Фигура Ф называется замкнутой, если она содержит свою границу. Таким образом, замкнутая фигура содержит все свои граничные точки.

Нетрудно доказать, что сфера S( O, R) с центром в точке O и радиусом R является границей фигуры U( O, R), рассмотренной выше, а шар с центром в точке O и радиусом R является замкнутой фигурой.

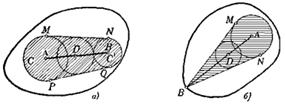
На рисунке 6 представлены выпуклые и невыпуклые фигуры.

Свойство 3. П ересечение двух выпуклых фигур является выпуклой фигурой.

Фигура Ф называется линейно связной, если любые две ее точки можно соединить ломаной, целиком содержащейся в этой фигуре. Ясно, что выпуклая фигура связна.

Открытая связная фигура называется областью. Например, фигура U( O, R), рассмотренная выше, является областью.

Фигура Ф называется ограниченной, если она целиком содержится в некотором шаре. Например, шар, куб являются ограниченными фигурами.

Наконец, дадим определения тела и его поверхности.

Телом называется ограниченная область вместе со своей границей. Граница тела называется его поверхностью.

Тема: Выпуклые многогранники и их свойства.

Основные вопросы, рассматриваемые на лекции:

1. Определение выпуклого многогранника.

2. Примеры выпуклых и невыпуклых многогранников.

2. Свойства выпуклых многогранников.

Краткое содержание лекционного материала

Примерами выпуклых многогранников являются: параллелепипед, тетраэдр, правильные призмы и пирамиды. Примерами невыпуклых многогранников являются: призмы и пирамиды, в основаниях которых лежат невыпуклые многоугольники, пространственный крест и др.

Рассмотрим некоторые свойства выпуклых многогранников.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.

Тема: Правильные и полуправильные многогранники

Основные вопросы, рассматриваемые на лекции:

1. Определение правильного многогранника.

2. Виды правильных многогранников.

3. Определение полуправильного многогранника.

4. Виды полуправильных многогранников.

Краткое содержание лекционного материала

Выпуклый многогранник называется правильным, если его гранями яв­ляются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней.

Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники. В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот мно­гогранник называется также правильным тетраэдром, или просто тетраэдром, что в переводе с греческого языка означает четырехгранник.

Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, называется октаэдром.

Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.

Заметим, что поскольку в вершинах выпуклого многогранника не мо­жет сходиться более пяти правильных треугольников, то других правиль­ных многогранников, гранями которых являются правильные треугольники, не существует.

Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба, других пра­вильных многогранников, у которых гранями являются квадраты не сущест­вует. Куб имеет шесть граней и поэтому называется также гексаэдром.

Поскольку в вершинах выпуклого многогранника не могут сходиться правильные многоугольники с числом сторон больше пяти, то других пра­вильных многогранников не существует, и таким образом, имеется только пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.

Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон), причем в каждой вершине сходится одинаковое число граней.

Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр и усеченный ико­саэдр.

Обратим внимание на то, что поверхность футбольно­го мяча изготавливают в форме поверхности усеченного икосаэдра. Из ку­ба и додекаэдра также можно получить усеченный куб и усе­ченный додекаэдр.

К последним двум многогранникам снова можно применить операцию усечения. Получим усеченный кубооктаэдр и усеченный икосо­додекаэдр.

Как видим, каждая поверхность этих многогранников состоит из двух или трех типов граней: квадраты, треугольники, пятиугольники и треу­гольники, квадраты, пятиугольники и треугольники. Модели этих многог­ранников будут особенно привлекательны, если при их изготовлении грани каждого типа раскрасить в свой особый цвет.

Тема: Звездчатые многогранники

Основные вопросы, рассматриваемые на лекции:

1. Правильные звездчатые многогранники.

2. Виды правильных звездчатых многогранников.

3. Звездчатые многогранники.

4. Примеры звездчатых многогранников.

Краткое содержание лекционного материала

Кроме правильных и полуправильных многогранников красивые формы имеют так называемые правильные звездчатые многогранники. Они получаются из пра­вильных многогранников продолжением граней или ребер аналогично тому, как правильные звездчатые многоугольники получаются продолжением сторон правильных многоугольников.

Первые два правильных звездчатых многогранника были открыты И. Кеплером (1571-1630), а два других почти 200 лет спустя построил французский математик и механик Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.

В работе «О многоугольниках и многогранниках» (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши (1789-1857). В работе «Исследование о многогранниках» он доказал, что других правильных звездчатых многогранников не существует.

При продолжении граней додекаэдра возникают две возможности. Во-первых, если рассматривать правильные пятиугольники, то получится так называемый большой додекаэдр. Если же, во-вторых, в качестве граней рассматривать звездчатые пятиугольники, то получается большой звездчатый додекаэдр.

Икосаэдр имеет одну звездчатую форму. При продолжении граней пра­вильного икосаэдра получается большой икосаэдр.

Таким образом, существуют 4 типа правильных звездчатых многогран­ников.

Кроме правильных звездчатых многогранников существуют и другие звездчатые формы, получающиеся продолжением граней правильных и полуправильных многогранников.

Так, продолжения граней кубооктаэдра приводят к четырем звездчатым многогранникам. Первый из них получается достраиванием на гранях кубооктаэдра треугольных пирамид и представляет собой соединение куба и октаэдра.

Следующая звездчатая форма кубооктаэдра образована из соединения куба и октаэдра добавлением 24 бипирамид.

Третья звездчатая форма кубооктаэдра представляет собой соединение шести четырехугольных пирамид, основаниями которых служат квадраты.

Последняя звездчатая форма кубооктаэдра является соединением звезды Кеплера и трех правильных четырехугольных призм, общей частью которых служит исходный куб.

Икосододекаэдр имеет 19 звездчатых форм. Наконец, икосаэдр имеет 59 звездчатых форм.

Источник

Задачи

Задача №1.1.1. Докажите, что пересечение двух или нескольких выпуклых фигур есть выпуклая фигура.

Задача №1.1.2. Докажите, что всякий выпуклый многоугольник является пересечением конечного числа полуплоскостей (рис.1.1.24). [8, 14]

Задача №1.1.3. Докажите, что

а) если А и В — внутренние точки выпуклой фигуры Ф, то все точки отрезка АВ — внутренние точки Ф;

б) если А — внутренняя, а В — граничная точка выпуклой фигуры Ф, то все точки отрезка АВ, кроме В,— внутренние точки Ф;

в) если А и В—граничные точки выпуклой фигуры Ф, то либо все точки отрезка АВ — граничные точки Ф, либо все точки отрезка АВ, кроме А и В,— внутренние точки Ф.

Задача №1.1.4. Докажите, что всякая прямая, проведенная через внутреннюю точку выпуклой фигуры, пересекает ее границу не более, чем в двух точках. Если выпуклая фигура ограничена, то каждая прямая, проходящая через какую-либо ее внутреннюю точку, пересекает границу фигуры ровно в двух точках.

Задача №1.1.5. Докажите, что если всякая прямая, проходящая через любую внутреннюю точку ограниченной фигуры, пересекает ее границу в двух точках, то фигура выпукла. [8, 15]

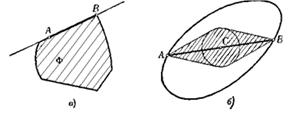
Задача №1.1.6. Докажите, что каждая из двух параллельных опорных прямых, расстояние между которыми имеет наибольшее возможное значение, содержит единственную точку границы фигуры и что отрезок, соединяющий эти точки, перпендикулярен к обеим опорным прямым (рис. 1.1.25). [8, 20]

Задача №1.1.7. Докажите, что наибольшее расстояние между двумя точками выпуклой фигуры совпадает с наибольшим расстоянием между парой параллельных опорных прямых.

Задача №1.1.8. Докажите, что если А и В — две точки выпуклой фигуры Ф, расстояние d между которыми имеет наибольшее значение, то прямые, проведенные через точки А и В перпендикулярно к отрезку АВ, являются опорными прямыми Ф. [8, 21]

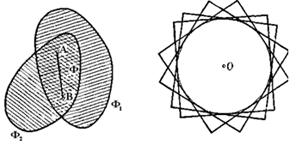
Пусть Ф₁ и Ф₂ — две выпуклые фигуры, Ф — их пересечение, А и В — две произвольные точки, принадлежащие пересечению Ф (рис. 1.1.26). По определению пересечения двух фигур обе точки А и В принадлежат как фигуре Ф₁, так и фигуре Ф₂. В силу выпуклости фигуры Ф₁ все точки отрезка АВ принадлежат Ф₁, а в силу выпуклости Ф₂ — все они принадлежат также фигуре Ф₂. Следовательно, отрезок АВ целиком принадлежит пересечению Ф фигур Ф₁ и Ф₂, а это и означает, что пересечение Ф выпукло.

Примечание. Теорема остается верной и в том случае, когда фигур Ф_1,…,Ф_n. бесконечно много; доказательство ее остаётся прежним. Например, на рис. 1.1.27 изображены равные между собой квадраты с общим центром. Легко видеть, что пересечением всех таких квадратов (а этих квадратов бесконечно много) является круг, т. е. выпуклая фигура.

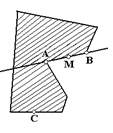
Выпуклый многоугольник Ф лежит по одну сторону от каждой прямой, являющейся продолжением его стороны. В самом деле, если бы существовала точка С, принадлежащая Ф и расположенная не с той стороны прямой АВ (А и В — две соседние вершины Ф), с какой многоугольник Ф примыкает к стороне АВ (рис. 1.1.28), то, например, отрезок МС, соединяющий внутреннюю точку М отрезка АВ с точкой С, не принадлежал бы целиком Ф, т. е. многоугольник Ф не мог бы быть выпуклым. Таким образом, выпуклый многоугольник Ф расположен целиком в каждой из полуплоскостей, границами которых служат прямые, содержащие каждую из сторон многоугольника. Пересечение всех таких полуплоскостей и дает многоугольник Ф.

а) Пусть А и В — две внутренние точки фигуры Ф. Согласно определению внутренних точек (определение1.1.4) существуют два круга С и С’ с центрами соответственно в точках А и В, все точки которых принадлежат фигуре Ф (рис. 1.1.29, а). Пусть МN и РQ — внешние общие касательные кругов С и С’. В силу выпуклости Ф вся криволинейная фигура МРQN, заштрихованная на рис. 1.1.29, а) принадлежит Ф, и следовательно, каждая точка D отрезка АВ является центром некоторого круга, все точки которого принадлежат Ф (этот круг вписан в фигуру МРQN).

б) Доказательство почти не отличается от доказательства пункта а), только окружность С’ приходится заменить одной точкой В и фигуру МPQN — фигурой MBN, заштрихованной на рис. 1.1.29, б).

в) Пусть А и В — две граничные точки выпуклой фигуры Ф. Отрезок АВ может целиком состоять из граничных точек (рис. 1.1.30, а) — это и есть первый случай, указанный в условии задачи.

Если же какая-либо точка С отрезка АВ является внутренней точкой Ф, то согласно пункту б) все точки отрезков СА и СВ, кроме А и В, должны быть внутренними для Ф — это второй случай, указанный в условии (рис. 1.1.30, б). [8, 140]

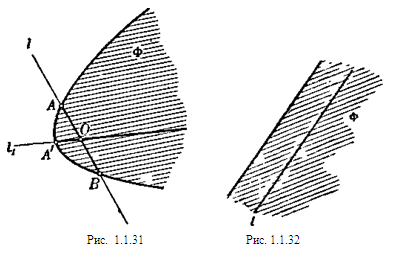
Пусть Ф это выпуклая фигура, О — ее внутренняя точка и l—прямая, проходящая через точку О. Так как прямая l сама является выпуклой фигурой, то ее пересечение с фигурой Ф будет (согласно задаче 1.1.1) выпуклой фигурой, расположенной на прямой (одномерной выпуклой фигурой), т. е. отрезком, лучом или всей прямой. Если это — отрезок, то его концы А и В являются граничными точками фигуры Ф (рис. 1.1.31), и следовательно, прямая l содержит две граничные точки Ф.

Если это пересечение — луч (прямая l₁ на рис. 1.1.31), то его начало А’ будет единственной граничной точкой фигуры Ф, лежащей на прямой l_1.

Если, наконец, прямая l целиком принадлежит фигуре (рис. 1.1.32), то на этой прямой нет ни одной граничной точки фигуры Ф.

Если фигура Ф ограничена, то ее пересечение с прямой также ограничено и, следовательно, является отрезком. Таким образом, на каждой прямой l, проведенной через внутреннюю точку ограниченной выпуклой фигуры Ф, имеются ровно две граничные точки этой фигуры. [8, 142]

Утверждение данной задачи равносильно утверждению, что для всякой ограниченной невыпуклой фигуры Ф найдется прямая, пересекающая ее границу более чем в двух точках. Докажем это.

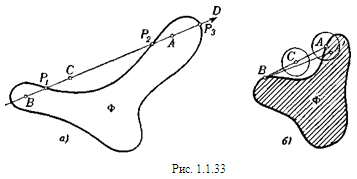
Пусть Ф — ограниченная невыпуклая фигура. В таком случае найдутся такие точки А и В, принадлежащие Ф, что отрезок, их соединяющий, не принадлежит целиком фигуре Ф; обозначим через С точку отрезка АВ, не принадлежащую Ф (рис. 1.1.33, а). Мы всегда можем предположить, что точка А — внутренняя точка Ф.

Действительно, если А — граничная точка Ф, А’ — внутренняя точка, достаточно близкая к точке А, то отрезок А’В также будет иметь точки вне фигуры Ф (рис. 1.1.33, б).

Итак, пусть А — внутренняя точка. На отрезке ВС есть граничная точка Р₁, фигуры Ф (может быть, совпадающая с В), т.к. точка В принадлежит фигуре Ф, а С лежит вне ее. На отрезке АС также есть граничная точка Р₂ фигуры Ф (А лежит внутри Ф, С— вне этой фигуры). Тогда, продолжив отрезок ВА за точку А, мы получим луч АD, исходящий из внутренней точки А фигуры Ф. На этом луче также есть граничная точка Р₃ фигуры Ф (т.к. фигура Ф ограничена).

Итак, на прямой АВ, проходящей через внутреннюю точку А фигуры Ф, лежат по крайней мере три граничные точки Р₁, Р₂ и Р₃, что и требовалось доказать. Следовательно, всякая фигура Ф, удовлетворяющая условию задачи, должна быть выпуклой.

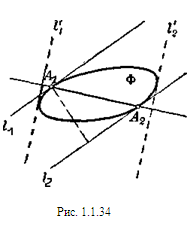
Пусть l₁ иl₂ — две параллельные опорные прямые фигуры Ф, расстояние между которыми имеет наибольшее значение; А₁ и А₂ — граничные точки фигуры Ф, принадлежащие соответственно прямым l₁ иl₂. Покажем, что отрезок А₁ А₂ перпендикулярен к обеим прямым l₁ иl₂. В самом деле, если бы это было не так, то расстояние между прямыми l₁ иl₂ было бы меньше, чем отрезок А₁А₂ (рис. 1.1.34), и тем более меньше, чем расстояние между двумя опорными прямыми l₁’и l₂ ’ фигуры Ф, перпендикулярными к отрезку А₁А₂, что противоречит условию (т.к. мы нашли две опорные прямые расстояние между которыми больше расстояния между опорными прямыми l₁ иl₂).

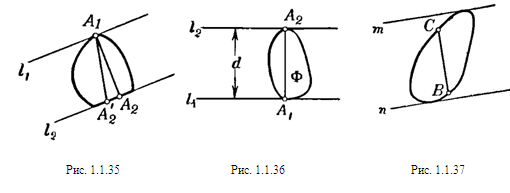
Так как А₁ и А₂ — какие угодно граничные точки фигуры Ф, принадлежащие соответственно прямым l₁ иl₂, то из перпендикулярности отрезка А₁А₂ к прямым l₁ и l₂ следует, что ни одна из прямых l₁ и l₂ не может иметь с фигурой Ф целый общий отрезок (т. е. случай, изображенный на рис. 1.1.35, невозможен); другими словами, каждая из этих прямых содержит единственную граничную точку фигуры Ф. [8, 143]

Пусть Ф — выпуклая фигура, l₁ и l₂ — параллельные опорные прямые, расстояние между которыми имеет наибольшее возможное значение d, А₁ и А₂ — общие точки фигуры Ф и прямых l₁ и l₂ соответственно. Так как отрезок А₁А₂ перпендикулярен к прямым l₁ и l₂ (см. задачу 1.1.6), то длина его равна d (рис. 1.1.36). Остается только доказать, что расстояние между любыми двумя точками фигуры Ф не превосходит d. Действительно, если В и С — какие-либо две точки фигуры Ф, а т и п — опорные прямые, перпендикулярные к прямой содержащей отрезок ВС (рис. 1.1.37), то отрезок ВС не превосходит расстояния между прямыми т и п, которое в свою очередь не превосходит d. Следовательно, длина ВС не может быть больше d.

Проведем две опорные прямые l и т выпуклой фигуры Ф, перпендикулярные к отрезку АВ. Вся фигура Ф заключена в полосе между прямыми l и т, а следовательно, в этой полосе помещается и отрезок АВ длины d, перпендикулярный к прямым l и т. Но так как расстояние между прямыми l и т не может быть больше d (задача 1.1.7), то прямые l и т должны проходить через концы А и В отрезка. [8, 145]

Источник