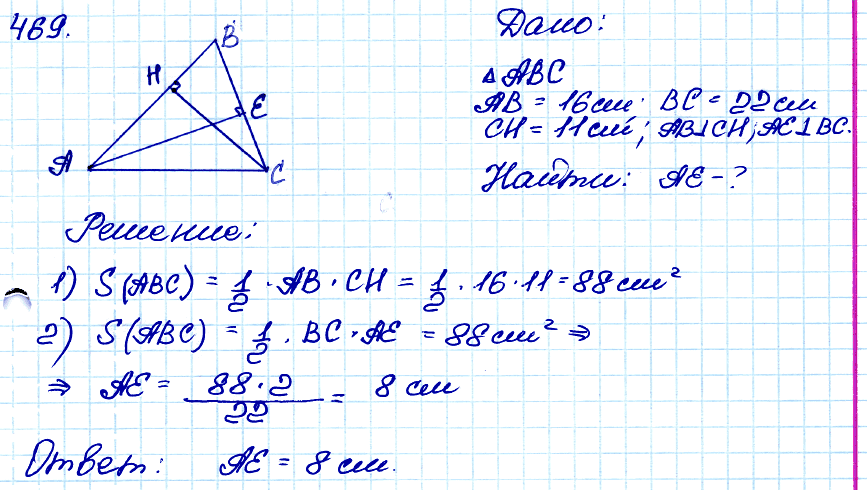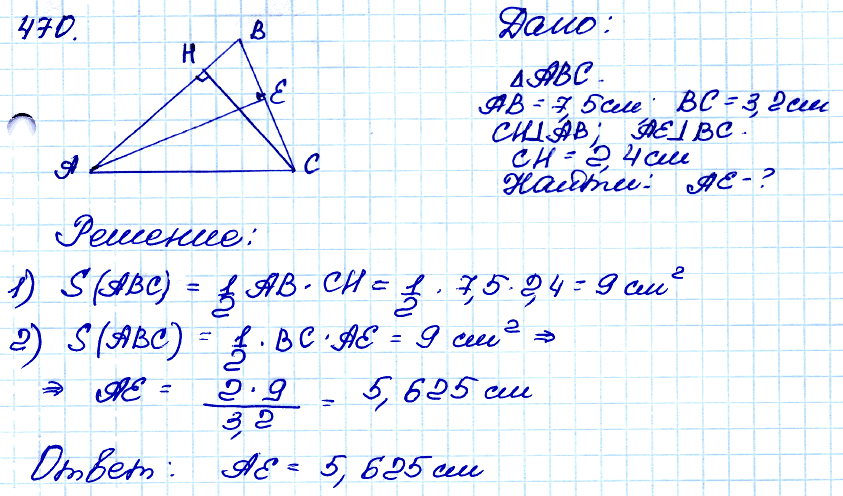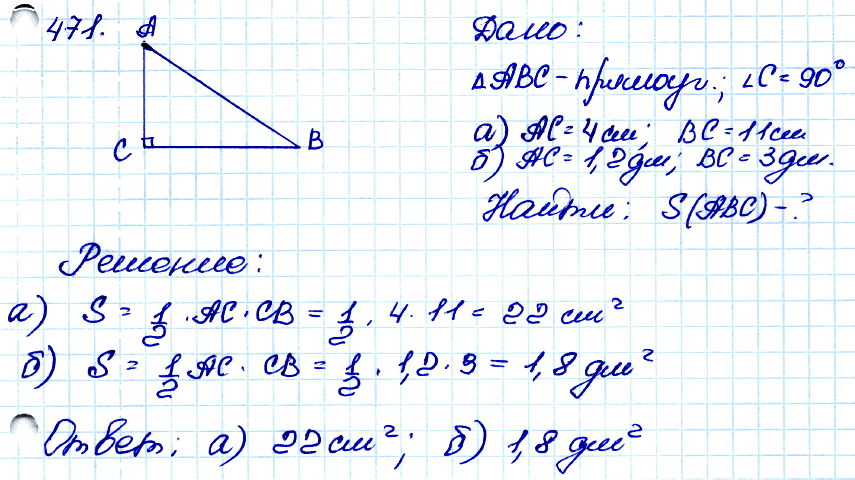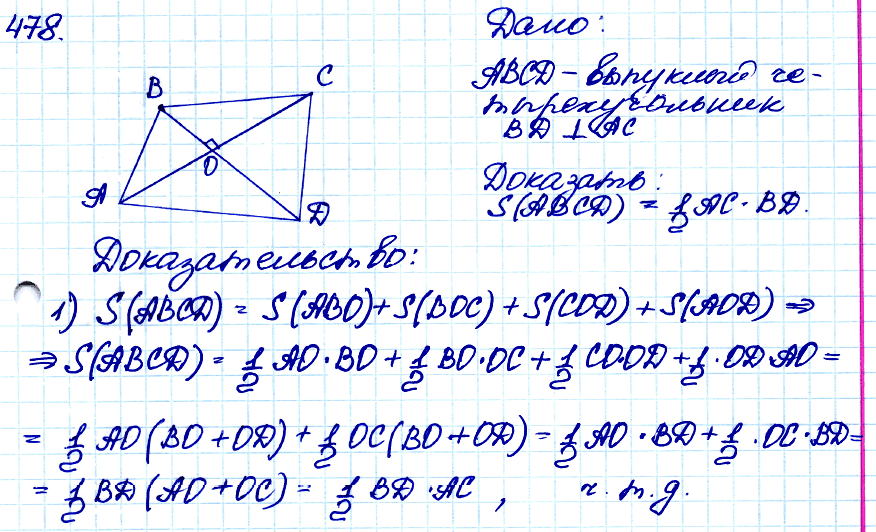докажите что площадь ромба равна половине произведения его диагоналей
Площадь ромба равна половине произведения его диагоналей
Здравствуйте!
Необходимо доказать, что площадь ромба равна половине произведения его диагоналей. Как можно подробнее.
Спасибо!
Задание.
Доказать, что площадь ромба равна половине произведения его диагоналей. 
Доказательство.
Построим ромб ABCD и проведем в нем диагонали АС и BD.
Необходимо доказать, что:
Диагонали параллелограмма (как и ромба, та как он и есть параллелограммом) пересекаются под прямым углом, а также при пересечении делятся пополам точкой пересечения (согласно свойству диагоналей). Получаем, что отрезки АО = CO и ВО = DO, углы между соседними из этих отрезков равны по 90 градусов. По свойству сторон ромба отрезки АВ, ВС, CD и AD равны.
Следовательно, треугольники АВО, СВО, CDO и ADO прямоугольные и равны по первому и третьему признаку.
Рассмотрим треугольник АВО.
Запишем формулу для вычисления площади этого треугольника через высоту и основание:
Как мы помним точка О делит диагонали ромба на две равные части, поэтому запишем:
Перепишем формулу площади АВО через диагонали ромба:
Диагонали ромба делят его на 4 равных треугольника с одинаковыми площадями. Тогда площадь ромба будет выражаться следующей формулой:
Мы получили, что площадь ромба действительно равна половине произведения диагоналей.
Доказательство завершено.
Геометрия 8 класс Атанасян Задачи 459-482
Упражнения 459-482 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия Атанасян. Глава 6.
§ 2. Площади параллелограмма,
треугольника и трапеции
Задачи №№ 459-482:
Задача № 460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
Задача № 461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.
Задача № 462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
Задача № 463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.
Задача № 465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
Задача № 466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.
Задача № 467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
Задача № 469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.
Задача № 470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.
Задача № 471. □ Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.
Задача № 473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
Задача № 474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
Задача № 475. □ Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.
Задача № 476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.
Задача № 478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
Задача № 480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD = 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.
Задача № 481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
Задача № 482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава VI. Площадь. § 2. Площади параллелограмма, треугольника и трапеции (52. Площадь параллелограмма. 53. Площадь треугольника. 54. Площадь трапеции). Геометрия 8 класс Атанасян Задачи 459-482 + ОТВЕТЫ.