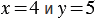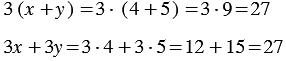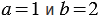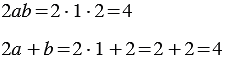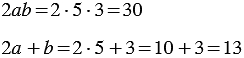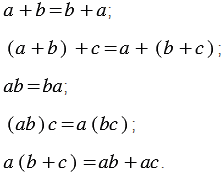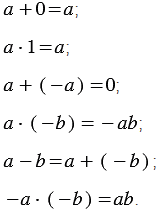докажите что при любых значениях переменных верно равенство
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 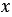
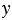

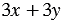
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 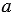
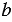
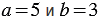
Мы получили разные результаты.
Следовательно, выражения 
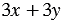
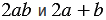
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 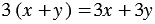
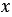
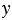
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 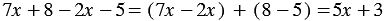
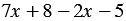
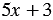
2) 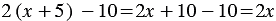
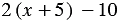
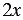
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 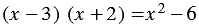
Решение: Приведем контрпример. Если 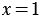
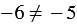
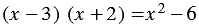
Поделись с друзьями в социальных сетях: