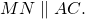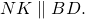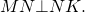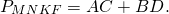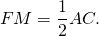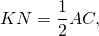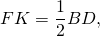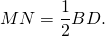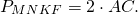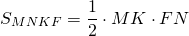докажите что середины сторон ромба являются вершинами прямоугольника
Середины сторон ромба — вершины прямоугольника
Доказать, что середины сторон ромба являются вершинами прямоугольника.
M, N, K, F — середины его сторон
Доказать : MNKF — прямоугольник.
1) По теореме Вариньона, MNKF- ромб.
2) Проведём диагонали AC и BD.
3) Рассмотрим треугольник ABC.
По условию, M и N — середины сторон AB и BC.
Значит, MN — средняя линия треугольника ABC (по определению).
4) Аналогично, в треугольнике BCD
Две прямые, соответственно параллельные перпендикулярным прямым, также перпендикулярны:
6) Имеем: в параллелограмме MNKF ∠MNK=90º.
Значит, MNKF- прямоугольник (по признаку).
Что и требовалось доказать.
Периметр прямоугольника MNKP равен сумме диагоналей ромба ABCD
Площадь прямоугольника MNKP равна половине площади ромба ABCD
Середины сторон прямоугольника — вершины ромба
Доказать, что середины сторон прямоугольника являются вершинами ромба.
Дано : ABCD — прямоугольник,
M, N, K, F — середины его сторон.
Доказать : MKNF — ромб.
1) Проведём диагонали AC и BD.
2) Рассмотрим треугольник ABC.
Так как F и M — середины AB и BC, FM- средняя линия треугольника ABC.
3) Аналогично, в треугольнике ADC
в треугольнике ABD
в треугольнике BCD
Значит, FM=MN=KN=FK. Следовательно, MNKF — ромб (по признаку).
По доказанному, сторона ромба равна половине диагонали прямоугольника. Следовательно, периметр ромба равен удвоенной длине диагоналям прямоугольника:
Площадь ромба равна половине произведения его диагоналей:
Диагонали ромба MNKF равны сторонам прямоугольника ABCD, следовательно, площадь ромба равна половине произведения сторон прямоугольника: