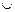докажите что симметрическая разность ассоциативна

Бинарные операции над упорядоченными множествами

В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.

I. Пересечение упорядоченных множеств

Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.

Сделал небольшую анимацию, чтобы показать как работает алгоритм.

Пример реализации на javascript:

Обращение к функции:

II. Разность упорядоченных множеств

Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

III. Объединение упорядоченных множеств

Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

IV. Симметрическая разность упорядоченных множеств

Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.

По сути это вычитание множеств, сначала A из B, затем B из A.

Источник

Фундаментальная система циклов

По этой ссылке вы найдёте полный курс лекций по математике:

Термин фундаментальная система (решений) используется для обозначения базиса в пространстве решений системы линейных однородных (алгебраических) уравнений, либо в пространстве решений однородного дифференциального уравнения. В каждом из этих случаев через элементы фундаментальной системы оказывается возможным выразить, и при том единственным образом, элементы некоторого бесконечного множества. В (конечном) графе число циклов конечно, но может быть достаточно велико (по сравнению с порядком графа).

Симметрическая разность множеств Симметрической разностью множеств А и В называют множество Фундаментальная система циклов Операция нахождения симметрической разности коммутативна: А Д В = В Д А (это очевидно) и ассоциативна: (попробуйте доказать это с помощью рис. 22). В силу ассоциативности при записи симметрической разности нескольких множеств скобки (указывающие порядок выполнения данной операции над множествами) можно не расставлять. А АВ Рис. 22.

Симметрическая разность двух и трех множеств Пусть А — произвольное множество. Множество всех подмножеств А с операцией симметрической разности (/3(Л), Д) образует коммутативную группу; в роли нейтрального элемента группы выступает пустое множество, каждый элемент группы является обратным самому себе. Лемма 3. При произвольном натуральном п симметрическая разность п множеств состоит в точности из тех элементов данных множеств, которые принадлежат нечетному их числу.

Доказательство проводится индукцией по числу множеств. База индукция очевидна. Индукционный шаг. Пусть доказываемое утверждение справедливо для всех п ^ к. Симметрическая разность к + 1 множеств имеет вид причем p,q ^ к, p + q = k+1. Множество В состоит из элементов, принадлежащих В\ (значит, по индуктивному предположению, принадлежащих нечетному числу множеств из) и не принадлежащих Bi (то есть входящих в четное число множеств из или, наоборот, не принадлежащие В\ и принадлежат** В2 (т. е. принадлежащих четному числу множеств из А\. АР и нечетному числу множеств из Ар+1. yAp+q).

Возможно вам будут полезны данные страницы:

Оказывается, множество всех псевдоциклов графа замкнуто относительно симметрической разности.

Лемма 4. Для любого натурального п сиюлетринеская разность п псевдоциклов есть псевдоцикл. м Доказательство ведется индукцией по п. База индукции (утверждение для п = 1) очевидна. Обоснование индукционного шага сводится к рассмотрению случая двух псевдоциклов. Пусть С\ и — псевдоциклы. Для произвольной вершины v графа обозначим через S,(tj) множество ребер цикла С,, инцидентных v (t = 1,2). Степени вершины v в графах ) равны мощностям множеств S\(v), соответственно.

Множество всех циклов такого вида <Се \ е е Е \ Г>будем называть фундаментмьной системой циклов графа G = (V, Е) относительно стягивающего дерева (V,T). Пример см. на рис.23. Теорема 14. Произвольный цикл С связного графа G = (V,E) представим в виде симметрической разности некоторых циклов из фундаментальной системы циклов G относительно любого стягивающего дерева (V, Т). Такое представление единственно и имеет вид: Мы докажем даже более сильное угверждение, считая С псевдоциклом. Пусть — связный граф, (V, Т) — некоторое фиксированное стягивающее дерево G. Ребра этого дерева будем называть ветвями, а остальные ребра графа G — хордами.

Заметим, что каждый цикл Се содержит ровно одну хорду, а именно — е. Поэтому в симметрической разности (различных) фундаментальных циклов, равной С, должны присутствовать все циклы, отвечающие хордам из С\Г, и только они. Таним образом, если представление псевдоцикла С в виде симметрической разности фундаментальных циклов существует, то оно единственно и имеет вид (1). Докажем теперь, что равенство (1) действительно имеет место.

Пусть По лемме 4 В — псевдоцикл; как уже показано, из хорд В содержит только хорды, принадлежащие С. Применяя леммы 3 и 4, получаем, что симметрическая разность ВАС — псевдоцикл, не содержащий хорд (так как каждая хорда одновременно либо принадлежит, либо не принадлежит В и С, т. е. число се вхождений в данные два множества четно); стало быть, В АС СТ. Осталось доказать, что в В Л С нет и ветвей.

не пуст, то согласно следствию 4 теоремы 9 он имеет не менее двух висячих вершин, в то же время — по определению псевдоцикла — он не содержит висячих вершин. Итак, мы выяснили: 2? Д С = 0, что равносильно совпадению множеств В = Д Се и С. Теорема доказана. На множестве всех псевдоциклов связного графа можно ввести структуру линейного пространства над полем GF<2), где в роли «сложения» выступает симметрическая разность, а умножение на скаляр определяется естественным образом — для произвольного псевдоцикла С имеем:

Если электрической цепи сопоставить граф, ребра которого соответствуют источникам ЭДС, сопротивлениям, индуктивностям и т.д., а вершины — узлам соединений элементов цепи, то при использовании закона Кирхгофа для напряжений, гласящего: сумма падения напряжений вдоль цикла равна нулю, необходимо найти фундаментальную систему циклов. Уравнения, отвечающие этим циклам, не будуг зависеть друг от друга, в то же время их выполнение будет гарантировать выполнение уравнений для всех циклов графа.

Возможно эта страница вам будет полезна:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Симметрическая разность

Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них. Симметрическая разность множеств и обозначается как В некоторых источниках используется другое обозначение:

Содержание

Определение

Симметрическую разность можно ввести двумя способами:

Понятие симметрической разности можно обобщить на число множеств, большее двух.

Свойства

Пример

См. также

Литература

Полезное

Смотреть что такое «Симметрическая разность» в других словарях:

СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — множеств одна из операций над множествами. Пусть имеются два множества Аи В. Тогда их симметрическая разность обозначается ADB и определяется равенствами где символы означают соответственно операции объединения, пересечения, разности и дополнения … Математическая энциклопедия

СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия

Разность множеств — Не следует путать с Симметрическая разность. Разность двух множеств это теоретико множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно… … Википедия

АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия

Симметричность — может означать: Симметрия Симметричная операция (от нескольких операндов) Симметричная функция (от нескольких переменных) Симметрический многочлен в математической логике: Симметричное отношение в линейной алгебре: Симметричный тензор… … Википедия

Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия

Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

ИСЧИСЛЕНИЕ КЛАССОВ — аксиоматич. (см. Аксиоматический метод) описание логики классов. И. к. рав нообъёмно исчислению одноместных предикатов (см. Логика предикатов): у этих исчислений совпадают классы как исходных формул, так и выводимых формул (теорем);… … Философская энциклопедия

Источник

Докажите что симметрическая разность ассоциативна

Объединение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y, т.е. принадлежат X или принадлежат Y.

Объединение X и Y обозначается через X∪Y

Формально x∈X∪Y ⇔ x∈X или x∈Y

Пример 3. Если X — множество точек левого круга и Y — множество точек правого круга, то

X∪Y — заштрихованная область, ограниченная обоими кругами.

представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств данной системы М.

Для объединенных множеств справедливы:

справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.

Очевидно, что X∪∅ = X. Отсюда можно видеть, что ∅ играет роль нуля в алгебре множеств.

2. Пересечение множеств

Пересечение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y.

Пересечение множеств обозначается X∩Y.

Формально x∈X∩Y ⇔ x∈X и x∈Y

Пример 5. Если Х — множество точек левого круга, а Y — множество точек правого круга, то X∩Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.

Множества X и Y называются непересекающимися (дизъюнктными), если они не имеют общих элементов, то есть если X∩Y=∅.

Частный случай: кортеж длины 1 —

кортеж длины 0 — или ∧ — пустой кортеж.

Отличие кортежа и обыкновенного множества: в кортеже могут быть одинаковые элементы.

Упорядоченные множества, элементами которых являются вещественные числа, будем называть векторами или точками пространства (n-мерного).

Два вектора равны, если они имеют одинаковую длину и соответствующие координаты их равны.

Компонентами кортежа (вектора) могут быть также компоненты кортежи (векторы):

Пример. Слова в предложении,

Прямое произведение множеств

Прямым (декартовым) произведением множеств X и Y называется множество, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая принадлежит множеству Y.

Пример 3. Пусть X и Y — отрезки вещественной оси. Прямое произведение X*Y изображается заштрихованным прямоугольником. См. рис. б).

Прямое произведение изменяется при изменении порядка сомножителей т.е.

Очевидно X*Y = ∅ ⇔ X = ∅ или Y = ∅.

Частным случаем прямого произведения является понятие степеней (декартовых) множества — прямое произведение одинаковых множеств

M s =M*M*. *M, M 1 =M, M 0 =∧.

Обычно R — множество вещественных чисел, тогда R 2 =R*R — вещественная плоскость и R 3 =R*R*R — трехмерное вещественное пространство.

Проекция множества.

Операция программирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.

Пусть M — множество, состоящее из кортежей длины S. Тогда пролинией множества M будем называть множество пролиний всех кортежей из М

Очевидно что если М=Х*Y то Пр₁М=Х, Пр₂М=Y

и если Q⊆Х*Y то Пр₁Q⊆Х и Пр₂Q⊆Y

Пусть V — множество векторов одинаковой длины S.

В общем случае Пр_iV — вовсе не обязательно прямое произведение: оно может быть подмножеством.

Источник

Свойства разности множеств

1. Разности:

A \ B = A \ (A B) и A \ (B C)=(A \ B) (A \ C).

Важно.

Операция разности определяется только для двух множеств. Эта операция двухместная и не коммутативная: .

2. Свойство симметрической разности:

.

Доказательство.

Доказательство этого свойства, как и других утверждений о равенстве каких-либо множеств, состоит в том, чтобы, предположив принадлежность некоторого элемента x множеству из левой части равенства, доказать, что этот же самый элемент принадлежит множеству, стоящему в правой части равенства и наоборот.

Пусть , что по определению симметрической разности означает, что x (A\B) (B \A). Здесь возможны два варианта: либо x (A \ B), либо x (B \ A). В первом случае мы получаем: x (A \ B) (x A и x B) (x A B и x A B), откуда очевидно следует, что x . Ситуация, когда x (B \ A), рассматривается аналогично.

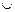
Итак, мы доказали, что если некоторый элемент x принадлежит множеству из левой части равенства, то из этого следует, что он принадлежит множеству, стоящему в правой части равенства. Теперь нам необходимо доказать обратное включение.

Пусть x (x A B и x A B). Здесь возможны две ситуации: либо и , либо и . Рассмотрим первый случай: пусть и , . Откуда .Второй случай доказывается аналогично.

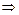
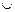
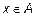
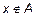
Важно.

Итак, мы полностью доказали заявленное свойство. При доказательстве подобных утверждений огромную роль играет то свойство, что если некоторый элемент x принадлежит некоторому множеству X, то он, очевидно, будет принадлежать и объединению множества X с произвольным другим множеством.

Определение 5.

Множество U, такое, что все рассматриваемые множества являются его подмножествами, называется универсальным.

То есть это множество, которое по предположению содержит все используемые нами множества. Обозначается не кругом, а прямоугольником (рис. 5).

Множества <звездные скопления>, <черные дыры>, <планеты>являются подмножествами универсального множества <вселенная>.

Определение 6.

Множество U \ A называется дополнением множества A (до универсального множества) и обозначается через .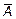

На кругах Эйлера это определение представлено на рис. 5.

Принцип двойственности

Теорема двойственности

Теорема 1 (двойственности или де-Моргана).

Пусть A_k, k = 1. n – некоторые подмножества универсального множества U, тогда имеют место следующие равенства:

; . (5)

Эти равенства, связывающие операции пересечения и объединения множеств и их дополнений до универсального множества, называют соотношениями принципа двойственности.

Доказательство.

.

Заметим, что в приведенном доказательстве все утверждения об элементе x соединены знаками , что позволяет одновременно строить доказательство утверждения в обе стороны.

Определим следующие множества: A – множество четных натуральных чисел; B – множество нечетных натуральных чисел; C – множество натуральных чисел, не больше 10. В качестве универсального множества мы будем рассматривать множество натуральных чисел N. Наша задача состоит в том, чтобы описать следующие множества:

.

– это множество нечетных натуральных чисел, т.е. множество B.

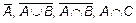
2. Каждое натуральное число является либо четным, либо нечетным, поэтому = .

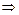
3. = . Следовательно, = N.

4. A C = < четные натуральные числа 10> = <2, 4, 6, 8, 10>.

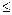
Базис операций

Если теперь считать, что в нашем распоряжении имеется универсальное множество U, то операции , , \ и можно определять друг через друга и фактически ввести некоторый базис операций в алгебре множеств.

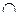
1. .

2. .

3. .

Определение 7.

Операции < , , \> называются булевыми операциями над множествами.

Источник