докажите что сумма углов треугольника равна 180
Докажите что сумма углов треугольника равна 180
Наглядная геометрия 7 класс. Опорный конспект № 4 Сумма углов треугольника.
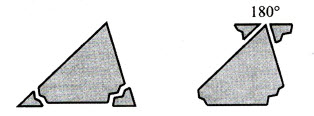
Великий французский ученый XVII века Блез Паскаль в детстве любил возиться с геометрическими фигурами. Он был знаком с транспортиром и умел измерять углы. Юный исследователь заметил, что у всех треугольников сумма трех углов получается одна и та же — 180°. «Как же это доказать? — подумал Паскаль. — Ведь нельзя же проверить сумму углов у всех треугольников — их бесконечное множество». Тогда он отрезал ножницами два уголка треугольника и приложил их к третьему углу. Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие. Дальнейшая судьба мальчика была уже предопределена.
В этой теме вы познакомитесь с пятью признаками равенства прямоугольных треугольников и, пожалуй, с самым популярным свойством прямоугольного треугольника с углом 30°. Оно звучит так: катет, лежащий против угла 30°, равен половине гипотенузы. Разделив равносторонний треугольник высотой, мы сразу получим доказательство этого свойства.
Сумма углов треугольника
ТЕОРЕМА. Сумма углов треугольника равна 180°. Для доказательства проведем через вершину прямую, параллельную основанию. Темные углы равны и серые углы равны как накрест лежащие при параллельных прямых. Темный угол, серый угол и угол при вершине образуют развернутый угол, их сумма 180°. Из теоремы следует, что углы равностороннего треугольника равны по 60° и что сумма острых углов прямоугольного треугольника равна 90°.
Внешним углом треугольника называется угол, смежный с углом треугольника. Поэтому иногда углы самого треугольника называют внутренними углами.
ТЕОРЕМА о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Действительно, внешний угол и два внутренних, не смежных с ним, дополняют закрашенный угол до 180°. Из теоремы следует, что внешний угол больше любого внутреннего, не смежного с ним.
ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. Отсюда следует: 1) Катет меньше гипотенузы. 2) Перпендикуляр меньше наклонной.
Расстояние от точки до прямой. Так как перпендикуляр меньше любой наклонной, проведенной из той же точки, то его длина принимается за расстояние от точки до прямой.
Неравенство треугольника. Длина любой стороны треугольника меньше суммы двух других его сторон, т. е. а
ТЕОРЕМА о свойстве катета, лежащего против угла 30°. Катет, лежащий против угла 30°, равен половине гипотенузы. Доказывается достроением треугольника до равностороннего.
ТЕОРЕМА о свойстве точек биссектрисы угла. Любая точка биссектрисы угла равноудалена от его сторон. Если точка равноудалена от сторон угла, то она лежит на биссектрисе угла. Доказывается проведением двух перпендикуляров к сторонам угла и рассмотрением прямоугольных треугольников.
Вторая замечательная точка. Биссектрисы треугольника пересекаются в одной точке.
Расстояние между параллельными прямыми. ТЕОРЕМА. Все точки каждой из двух параллельных прямых находятся на равном расстоянии от другой прямой. Из теоремы следует определение расстояния между параллельными прямыми.
Определение. Расстоянием между двумя параллельными прямыми называется расстояние от любой точки одной из параллельных прямых до другой прямой.
Подробные доказательства теорем


Это опорный конспект № 4 по геометрии в 7 классе «Сумма углов треугольника». Выберите дальнейшие действия:
Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
Разные способы доказательств теоремы «Сумма углов треугольника»
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа» с. Визинга
«Разные способы доказательства
теоремы о сумме углов треугольника».
Выполнил: Чередов С.С.,
учащийся 8 «а» класс
Руководитель: Пахомова Л. Я., учитель математики
«Величие человека – в его способности мыслить».
Б. Паскаль
Второй год мы изучаем предмет-геометрию. Эта наука изучает свойства геометрических фигур. На одном из уроков мы изучали теорему о сумме углов треугольника. И с помощью доказательства сделали вывод: сумма углов треугольника равна 180˚. Мне захотелось узнать, можно ли доказать эту теорему на практике, без доказательства.
Гипотеза: Предполагаю, что можно доказать теорему о сумме углов треугольника практически, то есть при помощи бумаги.
Объект исследования: сумма углов треугольника.
Предмет: сумма углов треугольника равна 180˚.
Цель проекта: доказать теорему при помощи использования бумаги.
1.Найти материал по данной теме, изучить литературу.
2.Убедиться на практике, можно ли доказать теорему при помощи бумаги.
3.Рассказать одноклассникам о новых способах доказательства теоремы.
Ожидаемые результаты : надеюсь, что новые способы доказательств данной теоремы заинтересует ребят и они поймут, что геометрия-это не нудная, а увлекательная наука.
Для достижения целей и задач я, много читал, искал необходимую информацию в разных источниках, общался с интересными мне людьми.
2.1.Историческая справка. В курсе геометрии 7 класса мы изучали теорему о сумме углов треугольника. Узнали, что эта теорема одна из важнейших теорем в геометрии.
Её доказательство приписывают древнегреческому математику Пифагору, жившему в V в. до н. э.
На уроке учительница доказала эту теорему несколькими способами, что меня очень удивило. Мне, казалось, что любое утверждение можно доказать только единожды. Меня заинтересовал этот факт. Могу ли я отыскать еще другие способы доказательства?
Я обратился в библиотеку за книгами по геометрии, поискал в интернете. И для себя нашел интересный факт:
В геометрии Лобачевского сумма углов треугольника всегда меньше 180.
В геометрии Евклида сумма углов всегда равна 180.
В геометрии Римана – сумма углов больше 180.
И во-вторых, я нашел еще другие способы доказательства этой теоремы.
2.1.1. Так в нашем учебнике «Геометрия 7-9» под редакцией А.С. Атанасян теорема доказывается, используя свойства параллельности прямых и понятие развернутого угла. (приложение 1)
2.1.2.А в некоторых школах страны геометрию изучают по учебнику
2.1.3. А еще раньше, геометрию изучали по учебнику А.П. Киселева 1961, автор предлагает доказательство, основанное на понятии развернутого угла. (приложение 3)
2.1.4.Используя свойства параллельности прямых. (приложение 1)
Можно конечно их доказать, но это не так интересно. Интереснее, когда результат получаешь на практике.
Найти сумму углов треугольника.
2.1.7. Используя перпендикулярность прямых. Его можно показать на практике
Измерение углов при помощи бумажного треугольника (1 способ)
1. Берём обычный лист бумаги.
2. Вырезаем из него произвольный треугольник.
3. Проводим в нём высоту к большей стороне.
4. Сгибаем правый угол к проведённой высоте
5. Повторяем это же действие с левым углом.
6.И ещё раз проделываем сгибание, но только уже верхнего угла к основанию перпендикуляра.
2.1.8.Измерение углов при помощи бумажного треугольника (2 способ)
1..На одной из сторон треугольника взять точку.
2ЮЧерез неё провести две параллельные линии.
3.Ножницами отрезать их.
4.Приложить к третьему углу.
5.Получим развернутый угол- его сумма равна 180 градусов
2.2.Практическое применение знаний.
Геометрия возникла и развивалась в связи с потребностями практической деятельности человека. При строительстве даже самых примитивных сооружений необходимо уметь рассчитывать, сколько материала уйдет на постройку, вычислять расстояния между точками в пространстве и углы между плоскостями. Развитие торговли и мореплавания требовало умений ориентироваться во времени и пространстве.
Свойство углов прямоугольного равнобедренного треугольника знал еще один из первых творцов геометрической науки древнегреческий ученый Фалес. Используя его, он измерял высоту египетской пирамиды по длине ее тени. По легенде, Фалес выбрал день и время, когда длина его собственной тени равнялась его росту, поскольку в этот момент высота пирамиды также должна равняться длине тени, которую она отбрасывает. Конечно, длину тени можно было вычислить от средней точки квадратной основы пирамиды, но ширину основы Фалес мог измерять непосредственно. Таким образом,
можно измерять высоту любого дерева.
Вывод: Теорему сумма углов треугольника равна 180 градусов можно доказать не только с помощью определений и теорем, но и на практике, то есть с помощью бумаги. Надеюсь, что при выполнении практических работ, ребята больше заинтересуются геометрией
Геометрия 7-9 Атанасян.
Геометрия 7-9 Погорелов.
Геометрия А.П. Киселев.
2.1.1. Так в нашем учебнике «Геометрия 7-9» под редакцией А.С. Атанасян теорема доказывается, используя свойства параллельности прямых и понятие развернутого угла.
2.1.4.Используя свойства параллельности прямых.
2.1.2.А в некоторых школах страны геометрию изучают по учебнику

Доказать: A + B + C = 180.
1. Через середину ВС проведем прямую АО, так что
2. Рассмотрим AOC = DOB (по 1-му признаку)
AOC = BOD ( как вертикальные), значит 1= 3, 2= 4, при секущей ВС по свойству паралельных прямых.
2.1.3. А еще раньше, геометрию изучали по учебнику А.П. Киселева 1961, автор предлагает доказательство основанное на понятии развернутого угла.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
Теорема о сумме углов треугольника
Теорема 1. Сумма углов треугольника равна 180°.
Доказательство. Рассмотрим произвольный треугольник ABC и докажем, что ∠ A + ∠ B + ∠ C = 180°.
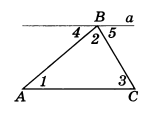
Проведем через вершину В прямую а, параллельную стороне АС (рис.1).
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому
∠ 4 = ∠ 1, ∠ 5 = ∠ 3. (1)
Очевидно, сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.
∠ 4 + ∠ 2 + ∠ 5 = 180°.
Отсюда, учитывая равенства (1), получаем:
∠ l + ∠ 2 + ∠ 3 = 180°, или ∠ A + ∠ B + ∠ C = 180°.
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
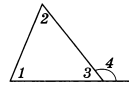
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказательство. Из равенств ∠ 4 + ∠ 3 = 180° и ∠ 1 + ∠ 2 + ∠ 3 = 180° (рис.2) получаем, что ∠ 4 = ∠ 1 + ∠ 2.
Пример 1. Два угла треугольника равны 27° и 41°. Найти третий угол и определить вид треугольника.
Пример 2. Какой вид имеет треугольник, в котором один угол равен сумме двух других углов?
Решение. Обозначим через х градусную меру того угла треугольника, который равен сумме двух других углов. Тогда, так как сумма углов треугольника равна 180°, то 2х = 180°, откуда х = 90°, т. е. треугольник прямоугольный.
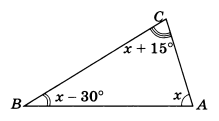
Пример 3. Найти углы треугольника ABC, зная, что угол С на 15° больше, а угол В на 30° меньше угла А.
Решая его, получаем х = 65°.
Таким образом, ∠ A = 65°, ∠ B = 35° и ∠ C = 80°.
Пример 4. В треугольнике ABC (рис.4) ∠ A = 60°, ∠ В = 80°.
Биссектриса AD этого треугольника отсекает от него треугольник ACD. Найти углы этого треугольника.
Геометрия. 7 класс
Конспект урока
Сумма углов треугольника
Перечень рассматриваемых вопросов:
Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.
Теоретический материал для самостоятельного изучения.
Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.
Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.
Сформулируем эту теорему.
Сумма углов треугольника равна 180°.
Проведем через вершину В прямую а ║АС.
∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.
Что и требовалось доказать.
Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.
Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠3 + ∠4 = 180° (по свойству развёрнутого угла).
∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.
Что и требовалось доказать.
Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Исходя из этого, можно классифицировать треугольники по углам.
По углам треугольник может быть:
‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);
‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);
‑ прямоугольным, если один угол 90° (т.е. прямой).
В прямоугольном треугольнике стороны имеют свои названия.
Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.
Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.
Сумма двух острых углов прямоугольного треугольника равна 90º.
∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°
Что и требовалось доказать.
Докажем, что в равностороннем треугольнике каждый угол равен 60 °.
Доказать: ∠А =∠С = ∠В = 60°.
Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.
∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠А = ∠С = ∠В = 180° : 3 = 60°.
Что и требовалось доказать.
Материал для углублённого изучения темы.
Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.
Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.
Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.
Разбор заданий тренировочного модуля
1. Чему равна градусная мера углаА, если треугольник АВС прямоугольный?
По условию, ∆АВС – прямоугольный → сумма его острых углов равна 90°.
2. По рисунку найдите угол N треугольника FNA.
По рисунку ∠NAP= 140°, этот угол внешний к углу А треугольника FNA→
∠NAP = ∠N +∠F= 140° (т.к. внешний угол треугольника равен сумме двух углов треугольника не смежных с ним).