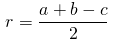докажите что в прямоугольном треугольнике гипотенуза больше катета
Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
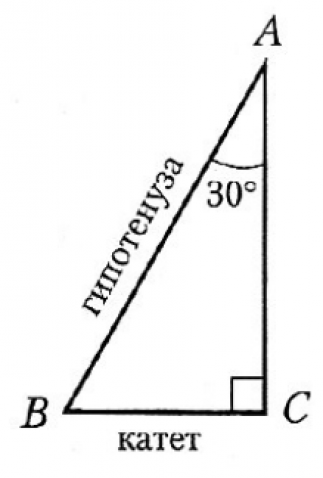
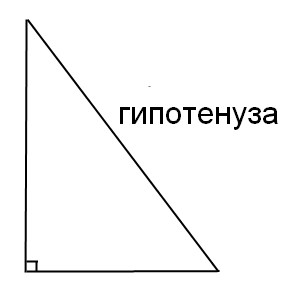
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
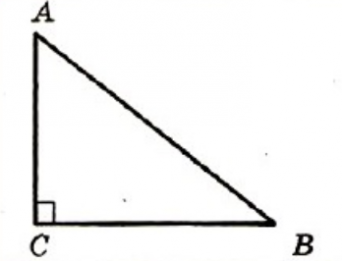
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Свойства прямоугольного треугольника
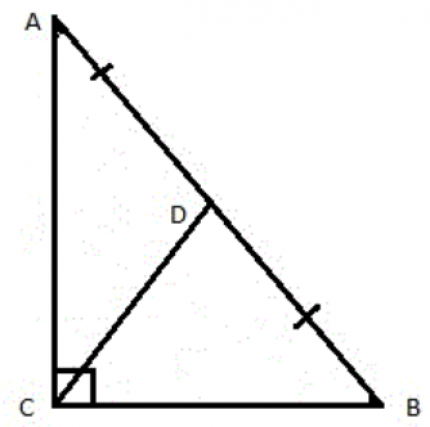
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
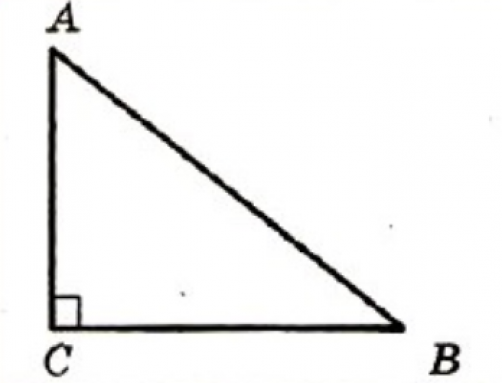
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Почему гипотенуза больше катета?
Почему в прямоугольном треугольнике гипотенуза всегда больше (или равна) катета?
В переводе с древнегреческого это слово означает натянутая. Скорее всего в древности что-то подобным образом натягивали. А равной катету гипотенуза быть не может. В этом случае один из катетов должен быть равен нулю. Но тогда это уже будет не треугольник, а просто прямой угол, с равными отрезками линий, отображающих этот угол.
Гипотенуза в прямоугольном треугольние лежит напротив самого большого угла в девяносто градусов. А два остальных угла дают столько же в сумме. А дальше для треугольников можно доказать, что чем больше угол, тем больше и сторона, напротив которой он расположен. Если треугольник вписать в круг, то самый большой угол будет опираться на самую большую дугу, а от этого и зависит размер хорды, которая Вляется стороной треугольника.
Чтобы лучше себе представить нужно нарисовать треугольник (он будет с одним прямым углом, который образован катетами).
Пусть этот треугольник стоит на одном из катетов. Можно прочертить воображаемую линию парралельную этому катету и проходящую через вершину, которая не соприкасается с этим катетом.
Квадрат гипотенузы равен сумме квадратов катетов. со школы наизусть. Это одно из тех правил, которые запомнились навсегда.)))
Как известно, площадь круга вычисляется по формуле:
То есть нам в любом случае нужно знать радиус.
Существует специальная формула нахождения радиуса вписанной в прямоугольный треугольник окружности:
В условии задачи даны только катеты, а для нахождения гипотенузы можно использовать теорему Пифагоа:
Например, катеты равны 3 и 4 см.
Найдём гипотенузу: √(3² + 4²) = √25 = 5 см.
Площадь круга будет равна:
C = πR² = 3,14 * 1 = 3,14 см².
Треугольник АВС, треугольник ЕНК.
Угол В = углу Н = 90*.
Длина катета в прямоугольном треугольнике равна корню из разности квадрата длины гипотенузы и квадрата длины второго катета.
В данном случае понятие «прилежащий» вообще ни к чему, поскольку катет может быть прилежащим (или противолежащим) только к углу, а углы для определения длины катетов знать совсем необязательно. Обычно их (то есть углы) используют в тригонометрии для определения синусов, косинусов, тангенсов и котангенсов. Если, конечно, я ничего не путаю, так как школу закончила лет эдак 20 назад.