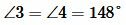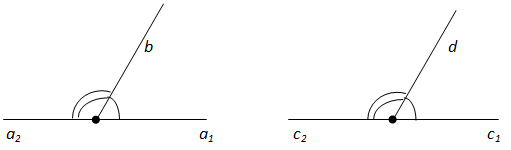докажите что вертикальные углы равны
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
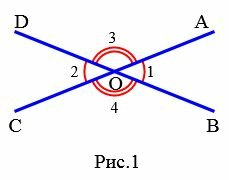 |
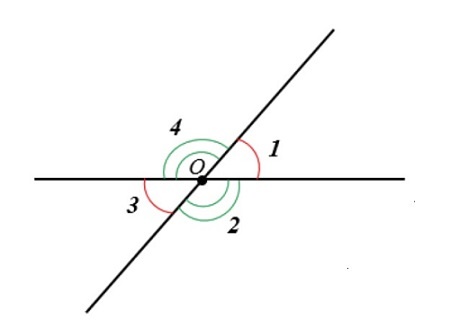
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
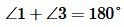 , , 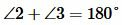 |
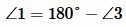 , , 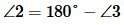 |
Следовательно 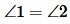
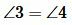
Задачи и решения
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
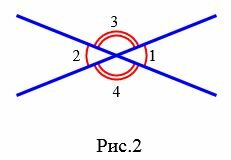 |
Решение. Так как углы 1 и 2 вертикальны, то 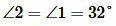
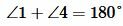
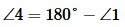 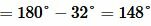 . . |
Углы 3 и 4 вертикальные. Тогда
Ответ. 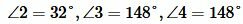
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Ответ. 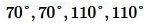
Геометрия. 7 класс
Конспект урока
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Давайте докажем это свойство.
Укажем ещё одно свойство смежных углов.
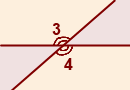
Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.
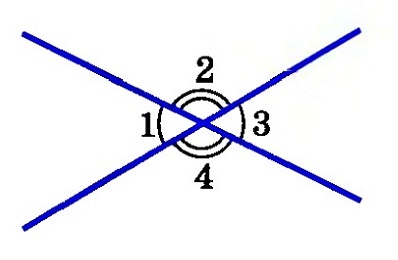
Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.
№3. Тип задания: выделение цветом.
Выделите верный ответ из списка:
60 0 ; 30 0 ; 75 0 ; 90 0
Вертикальные углы
Какие углы вертикальные? Каким свойством обладают вертикальные углы?
Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.
Определение.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
При пересечении двух прямых образуется две пары вертикальных углов:
∠1 и ∠2 — вертикальные углы
∠3 и ∠4 — вертикальные углы
Свойство вертикальных углов.
Вертикальные углы равны.
Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.
1) Сумма вертикальных углов равна 140º. Найти эти углы.
Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.
2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.
При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.
Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.
А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.
Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.
Какие углы называются вертикальными: определение и свойства
Вертикальные углы — что это такое в геометрии, определение
Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого. Иными словами – они противоположны.
Свойства вертикальных углов
Равны или нет, доказательство теоремы
Особенность вертикальных углов в том, что они абсолютно идентичны.
Убедимся в справедливости этого свойства. Докажем его: на чертеже 1 и 2, 2 и 3, 3 и 4, 4 и 1 являются смежными, 1 и 3, 2 и 4 – вертикальные.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(\angle1+\angle2=180^\circ и \angle2+\angle3=180^\circ\)
Отсюда выведем, что:
Уравнение доказало равенство углов 1 и 3.
Примеры решения задач
Задача 1
Дано
Найти: значения \(\angle2, \angle3, \angle4\)
Решение
\(\angle1\) и \(\angle3\) вертикальные. Значит \(\angle1=\angle3=45^\circ.\)
\(\angle1\) и \(\angle4\) смежные. По правилу о смежных углах:
Так как \(\angle4\) и \(\angle2\) вертикальные, то \(\angle4=\angle2=135^\circ.\)
Ответ: величина \(\angle3=45^\circ,\) величина \(\angle2\) и \(\angle4=135^\circ.\)
Задача 2
Дано
Две прямые пересеклись и сформировали четыре угла. Сумма двух из них составляет \(140^\circ.\)
Найти: значения всех углов, образовавшихся при пересечении прямых.
Решение
Так как вертикальные углы равны, то значение каждого из них соответствует:
Оставшиеся углы – смежные к вертикальным и вертикальные по отношению друг к другу. Для того, чтобы их вычислить, выполним следующее действие:
Докажите что вертикальные углы равны
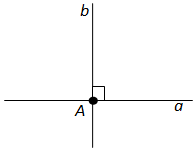
Вопрос 1. Какие углы называются смежными?
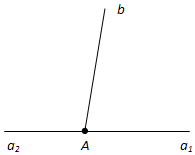
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a1b) и (a2b) смежные. У них сторона b общая, а стороны a1 и a2 являются дополнительными полупрямыми.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
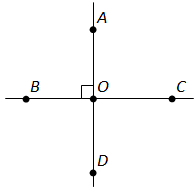
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
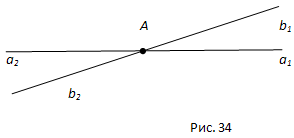
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a1b1) и (a2b2)- данные вертикальные углы (рис. 34). Угол (a1b2) является смежным с углом (a1b1) и с углом (a2b2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a1b1) и (a2b2) дополняет угол (a1b2) до 180°, т.е. углы (a1b1) и (a2b2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
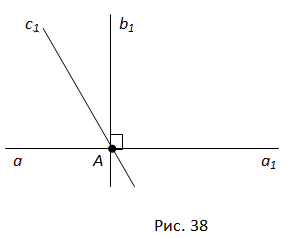
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b1.
Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a1. Но от полупрямой a1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
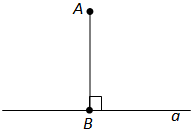
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.